699. 掉落的方块

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 positions[i] = [left(i), sideLength(i)] 表示：第 i 个方块边长为 sideLength(i) ，其左侧边与 x 轴上坐标点 left(i) 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例 1：

输入：positions = [[1,2],[2,3],[6,1]] 输出：[2,5,5] 解释： 第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。 第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。 第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。 因此，返回 [2, 5, 5] 作为答案。

示例 2：

输入：positions = [[100,100],[200,100]] 输出：[100,100] 解释： 第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。 第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。 因此，返回 [100, 100] 作为答案。 注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

提示：

• 1 <= positions.length <= 1000

• 1 <= left(i) <= 10(8)

• 1 <= sideLength(i) <= 10(6)

离散化+暴力

1.

对于每一个position值,[1,2]表示[1,1+2]区间上落下一个边长为2的正方形.

[2,3]表示[2,2+3]区间上落下一个边长为3的正方形.

[6,1]表示[6,6+1]区间上落下一个边长为3的正方形.

2.

对于每一个position值,可以抽象出左右边界和正方形的边长.[left,right],边长h.

maxcount数组存储每个点上的最大高度.

由于点没有办法表示图像,长度.因此可以定义index表示[index,index+1)的区间.

maxcount[1]=2,表示[1,2)区间上最大的高度是2.以此类推

那么对于每一个position,position[i][0]==left,position[i][0]+position[i][1]-1==right.边长为position[i][1].

3.

只需要对于每一个position方块,遍历left到right找到最大值记为maxh,此时更新left到right所有值为maxh+position[i][1].

然后把此时所有区间的最大高度值尾插到ret数组中.

因此还需要一个变量存储所有区间的最大高度值.

离散化

1.

我们知道所有方块对应的下标,第一个方块对应的left,right,第二个方块对应的left,right......

将这些下标排序+去重.存储到map中.

也就是直接将这些数据加入到map中即可,因为map自动排序+去重.

2.

将所有需要用到的下标,point加入到map后,依次给这些数据设置映射值,第一个元素映射0,第二个元素映射1,第三个元素映射3,以此类推.

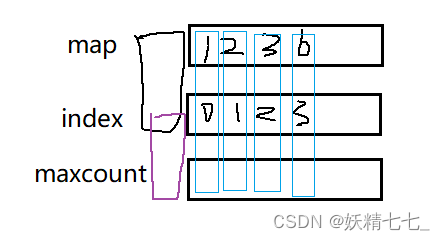
压缩坐标.因为原来的point的值我们并不关心是多少,我们只关心每一个point有一个maxcount记录最大值.

因此对于每一个point映射下标,对应maxcount的下标.

暴力

然后暴力求解即可.

class Solution {
public:vector<int> fallingSquares(vector<vector<int>>& positions) {map<int, int> nums_index; // 使用map来记录每个方块的左右边界对应的高度索引vector<int> ret; // 存储结果的数组for (auto& x : positions) {nums_index[x[0]]; // 记录左边界对应的高度索引nums_index[x[0] + x[1] - 1]; // 记录右边界对应的高度索引}int index = 0;for (auto& x : nums_index) {x.second = index++; // 为所有的高度索引分配唯一的编号}vector<int> maxcount(index); // 存储每个高度索引对应的最大高度int maxh = INT_MIN;for (auto& x : positions) {int left = nums_index[x[0]]; // 获取左边界对应的高度索引int right = nums_index[x[0] + x[1] - 1]; // 获取右边界对应的高度索引int max1 = INT_MIN;for (int i = left; i <= right; i++) {max1 = fmax(maxcount[i], max1); // 找到左右边界中的最大高度}int newh = max1 + x[1]; // 计算掉落后的新高度for (int i = left; i <= right; i++) {maxcount[i] = newh; // 更新每个高度索引对应的高度}if (newh > maxh)maxh = newh; // 更新最大高度ret.push_back(maxh); // 将最大高度加入结果数组}return ret; // 返回结果数组}
};

离散化+线段树

线段树

在暴力过程中,我们遍历left到right区间找区间最大值,然后全部加上边长,再把所有区间的最大高度尾插到ret数组中.

我们暴力查询区间max,暴力更新区间所有值.时间复杂度是O(N).

线段树优化这两个过程,线段树区间查询和区间更新操作都是O(logN).

线段树代码分析

1.

成员变量,一般来说要有一个arr数组,对应nums数组,区别是arr数组元素下标从1开始,也就是0位置不用,从1开始的元素依次对应nums数组的值.

size遍历存储数组大小.

treenode表示树的节点信息.

tree表示arr数组对应的线段树结构.

2.

treenode节点信息,maxh对应线段树区间查询的信息.

int change; // 变化值 int isupdate; // 是否需要更新

对应线段树区间更新的操作

表示任务值,和任务是否存在.

3.

pushup函数,用已经维护好的左右孩子信息,维护当前节点的信息.

维护的信息是线段树区间查询的信息.

4.

pushdown函数,用于下发一层任务,如果当前节点有任务,就下发,下发任务需要更新左右孩子的信息.

线段树区间查询的信息以及有关任务的信息.

也就是treenode中所有的信息.

5.

query查询函数,树结构对应是递归函数,用于查询L~R区间中的sum元素和.

如果当前节点对应的区间是L~R的一部分,返回当前节点的sum值.

如果当前节点和L~R没有重叠,return 0.

如果当前节点和L~R有一部分重叠,return 左孩子中某个节点区间是L~R一部分的sum值.或者renturn 右孩子中某一个节点区间是L~R一部分的sum值.

请注意,确保能够准确的实现递归逻辑,递归查询,去孩子节点查询的时候,必须把当前任务下发.如果有任务就下发,没有任务就不下发.

6.

update区间更新函数,树结构对应是递归函数,用于表示L~R区间更新为C.

如果当前节点对应的区间是L~R的一部分,维护当前节点所有查询信息和此次操作的信息.

如果当前节点和L~R没有重叠,return .表示不需要维护信息

如果当前节点和L~R有一部分重叠,更新左子树,更新右子树,更新自己.

同样的更新左右子树的时候,需要把旧任务下发一层.再更新

class SegmentTree {
public:int size; // 线段树数组的大小struct treenode {int maxh; // 节点对应的最大高度int change; // 变化值int isupdate; // 是否需要更新};vector<treenode> tree; // 线段树节点数组void pushup(int i) { // 更新父节点的最大高度tree[i].maxh = max(tree[i << 1].maxh, tree[i << 1 | 1].maxh);}void pushdown(int i) { // 下推更新if (tree[i].isupdate) {tree[i << 1].maxh = tree[i << 1 | 1].maxh = tree[i].change;tree[i << 1].change = tree[i << 1 | 1].change = tree[i].change;tree[i << 1].isupdate = tree[i << 1 | 1].isupdate = true;tree[i].isupdate = false;}}int query(int L, int R) { // 查询return _query(L + 1, R + 1, 1, size - 1, 1);}
private:int _query(int L, int R, int l, int r, int rt) { // 内部查询函数if (r < L || R < l) return 0;if (L <= l && r <= R) {return tree[rt].maxh;}pushdown(rt);int mid = (l + r) >> 1;return max(_query(L, R, l, mid, rt << 1), _query(L, R, mid + 1, r, rt << 1 | 1));}
public:void update(int L, int R, int C) { // 更新_update(L + 1, R + 1, C, 1, size - 1, 1);}
private:void _update(int L, int R, int C, int l, int r, int rt) { // 内部更新函数if (r < L || R < l) return;if (L <= l && r <= R) {tree[rt].maxh = C;tree[rt].isupdate = true;tree[rt].change = C;return;}pushdown(rt);int mid = (l + r) >> 1;_update(L, R, C, l, mid, rt << 1);_update(L, R, C, mid + 1, r, rt << 1 | 1);pushup(rt);}
public:SegmentTree(int n) { // 构造函数size = n + 1;tree.resize(size << 2);}
};class Solution {
public:vector<int> fallingSquares(vector<vector<int>>& positions) {// 初始化操作int n = positions.size();map<int, int> point_index; // 统计点的索引for (auto& x : positions) {point_index[x[0]];point_index[x[0] + x[1] - 1];}int index = 0;for (auto& x : point_index) {x.second = index++;}SegmentTree t(point_index.size()); // 初始化线段树// 开始解题vector<int> ret; // 存储结果的数组int maxh = INT_MIN;for (auto& x : positions) {int left = point_index[x[0]]; // 获取左边界对应的高度索引int right = point_index[x[0] + x[1] - 1]; // 获取右边界对应的高度索引int h = x[1]; // 方块高度int cur_maxHight = t.query(left, right); // 查询当前区间的最大高度cur_maxHight = cur_maxHight + h; // 计算新高度maxh = max(maxh, cur_maxHight); // 更新最大高度ret.push_back(maxh); // 将最大高度加入结果数组t.update(left, right, cur_maxHight); // 更新区间}return ret; // 返回结果数组}
};

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！