DFS与回溯专题:路径总和问题
一、路径总和
题目链接: 112.路径总和
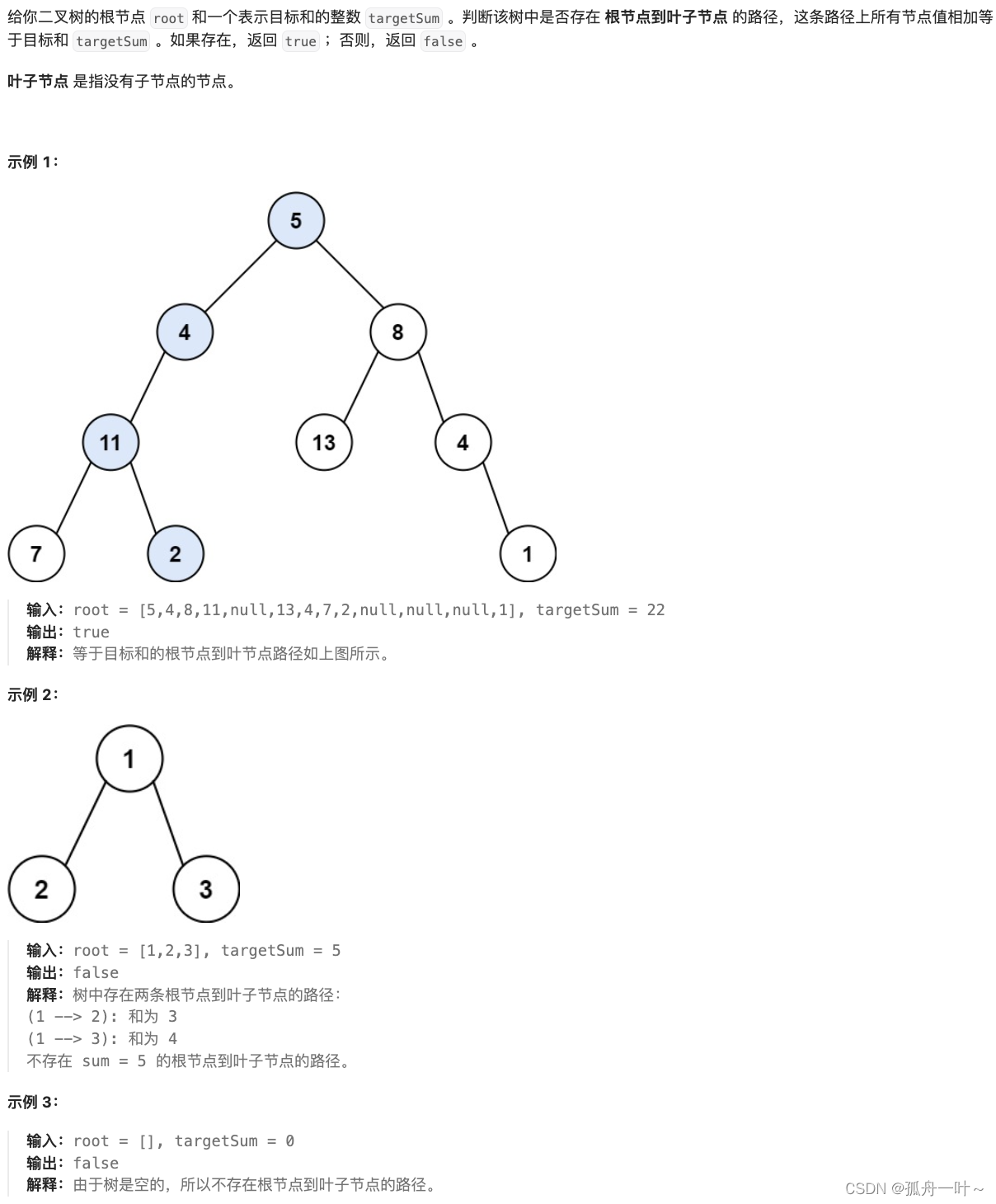
题目描述
代码思路
对二叉树进行dfs搜索,递归计算每条路径的节点值之和,当某个节点的左右子节点都为空时,说明已经搜索完成某一条路径,将它与目标值进行比较,若相等,则为true。
代码纯享版
class Solution {public int judge = 0;public boolean hasPathSum(TreeNode root, int targetSum) {int sum = 0;dfs(root, targetSum, sum);return judge == 1;}void dfs(TreeNode root, int targetSum, int sum){if(root == null) return;sum += root.val;if(root.left == null && root.right == null){if(sum == targetSum) judge = 1;return;}dfs(root.left, targetSum, sum);dfs(root.right, targetSum, sum);}
}
代码逐行解析版
class Solution {public int judge = 0; //用于判断是否存在符合题目要求的路径public boolean hasPathSum(TreeNode root, int targetSum) {int sum = 0; //用来统计路径上的节点值dfs(root, targetSum, sum); //对二叉树进行dfs搜索return judge == 1; //如果judge等于1,返回true;否则返回false}void dfs(TreeNode root, int targetSum, int sum){if(root == null) return; //节点为空,直接返回sum += root.val; //将该节点的值加入sum中if(root.left == null && root.right == null){ //该节点的左右子节点都为空时,说明搜索到了一条完整的路径if(sum == targetSum) judge = 1; //如果sum与目标和相等,judge变成1return;}//到这一步说明路径还没搜索完,接下来搜索该节点的左右子节点dfs(root.left, targetSum, sum);dfs(root.right, targetSum, sum);}
}
代码有关问题的解释
统计时sum的数值为什么不需要进行清零之类的操作?
递归是「隐式」回溯:使用一个整型变量(比如sum)来累加路径上的节点值,则在递归的过程中就不需要显式地进行撤回操作了。这是因为每次递归调用时,sum的值是通过参数传递的,每一层的递归调用都有自己的sum副本,这些副本互不影响。
二、路径总和 II
题目链接: 113.路径总和 II
题目描述

代码思路
算法流程:
函数 pathSum(root, targetSum) :
初始化: 结果列表 list_all ,路径列表 list 。
返回值: 返回 list_all 即可。
函数 dfs(root, targeSum,sum):
递推参数: 当前节点 root ,当前目标值 sum == targetSum 。
终止条件: 若节点 root 为空,则直接返回。
递推工作:
路径更新: 将当前节点值 root.val 加入路径 list 。
目标值更新: sum += root.val
路径记录: 当 root 为叶节点 且 路径和sum等于目标值 ,则将此路径 list 加入 list_all 。
先序遍历: 递归左 / 右子节点。
路径恢复: 向上回溯前,需要将当前节点从路径 list 中删除,即执行list.remove(list.size() - 1) 。
#代码纯享版
class Solution {public List<List<Integer>> list_all = new ArrayList();public List<Integer> list = new ArrayList();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {int sum = 0;dfs(root, targetSum, sum);return list_all;}void dfs(TreeNode root, int targetSum, int sum){if(root == null){return;}sum += root.val;list.add(root.val);if(root.left == null && root.right == null && sum == targetSum){list_all.add(new ArrayList(list)); }dfs(root.left, targetSum, sum);dfs(root.right, targetSum, sum);list.remove(list.size() - 1);}
}
代码逐行解析版
class Solution {public List<List<Integer>> list_all = new ArrayList(); //记录所有符合条件的路径public List<Integer> list = new ArrayList(); //记录搜索过程中的路径public List<List<Integer>> pathSum(TreeNode root, int targetSum) {int sum = 0; //用来统计路径上的节点值dfs(root, targetSum, sum); //对二叉树进行dfs搜索return list_all; //返回路径的列表}void dfs(TreeNode root, int targetSum, int sum){if(root == null){ //节点为空,直接返回return;}sum += root.val; //将该节点的值加入sum中list.add(root.val); //将节点添加到路径中if(root.left == null && root.right == null && sum == targetSum){ //如果路径走完且与目标值相同list_all.add(new ArrayList(list)); //将路径添加到list_all(浅拷贝)}//到这一步说明路径还没搜索完,接下来搜索该节点的左右子节点dfs(root.left, targetSum, sum);dfs(root.right, targetSum, sum);//删掉路径列表中最后一个节点list.remove(list.size() - 1);}
}
代码相关问题的解释
为什么要写list_all.add(new ArrayList(list)),而不是list_all.add(list)?
注意:解释里面的sum.add(path)就是list_all.add(list)



![[Flutter3] Json转dart模型举例](https://img-blog.csdnimg.cn/direct/024da5ebeafd43599f3fe01d1f59061d.png)