蚁群算法是一种模拟自然界中蚂蚁觅食行为的优化算法,常用于解决路径规划问题。在栅格路径优化中,蚁群算法可以帮助找到从起点到终点的最优路径。以下是蚁群算法栅格路径优化的基本流程步骤:
-
初始化参数:
(1)设置蚂蚁数量(popsize)、信息素挥发系数(ρ)、信息素增强系数(Q)、最大迭代次数、信息素重要程度因子(α)、启发函数重要程度因子(β)。
(2)初始化信息素矩阵,设置为一个相同的较小正值,避让0.01。
(3)定义栅格地图,包括障碍物、可行走区域等。 -
蚂蚁路径选择:
(1)每只蚂蚁从起点开始,根据转移概率公式选择下一个要移动的栅格。转移概率基于当前栅格与相邻栅格之间的信息素浓度和启发式信息,表达式如下:
(1)式表示蚂蚁在t时刻由城市i选择城市j的概率。α是信息素在概率计算中的权重,它的值越大,信息素在蚂蚁选择下一个要到的城市中起到的作用越大。β是启发因子(在路径问题中常以d的倒数来表示)在概率计算中所占的权重,它的值越大,启发因子在蚂蚁选择城市的过程中所起的作用越大,allowed是不在蚂蚁禁忌表中的城市集合(在栅格问题中就是非障碍物和未走过的栅格的节点编号集)。
(2)更新所选路径上的信息素浓度,通常包括信息素的挥发和增加:
其中表示在t+1次迭代时边ij上的信息素. ρ是信息素维持因子, 1-ρ是信息素挥发因子.
是所有蚂蚁在边ij上所释放的信息素的总和:
-
计算路径长度:
当所有蚂蚁都完成一次路径搜索后,计算每只蚂蚁所走路径的总长度。 -
更新信息素:
根据每只蚂蚁的路径长度和设定的规则,更新栅格地图上的信息素浓度。优质路径上的信息素会得到增强,而劣质路径上的信息素会逐渐挥发减少。
-
迭代优化:
重复步骤2至4,进行多次迭代,直到达到最大迭代次数或满足其他停止条件。 -
选择最优路径:
在所有蚂蚁走过的路径中,选择长度最短(或成本最低)的路径作为最优路径。 -
输出结果:
输出最优路径及其长度。
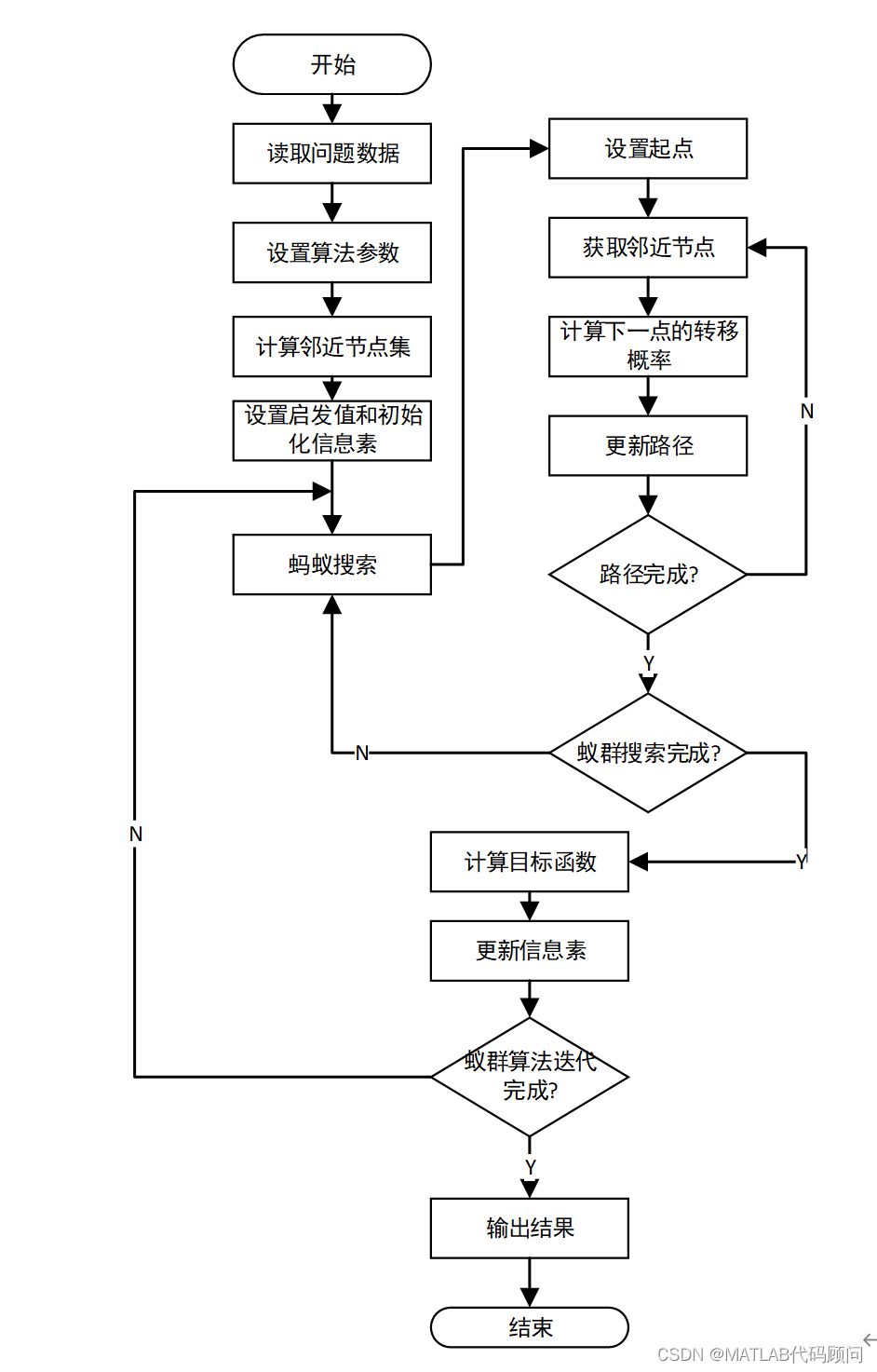
流程图如下:
本算法的关键在于邻近节点集的概念和数据设计
首先对整个场景进行栅格化, 并依次编号,如下表所示
| 7 | 8 | 9 |
| 4 | 5 | 6 |
| 1 | 2 | 3 |
然后构造一个cell变量nearcell或者一个邻接指示矩阵E
nearcell{1,1}=[2,4,5];
nearcell{2,1}=[1,3,4,5,6];
nearcell{3,1}=[2,5,6];
…
对于每一个i都有nearcell{i,1}=nearmat
nearmat是与节点i相邻的节点编号集合, 当然这个不能人工一个一个设定, 必须采用代码来自动设定, 根据栅格的特点, 我们可以用代码实现 ,其原理为:
对于任何一个栅格中的节点(如节点5),其周边有8个邻近节点(如果是在边界,则代码在后面进行了边界约束),其行号和列号与节点的行列号是有规律的,因此可以采用代码进行设置。具体实现如nearfun函数所示。
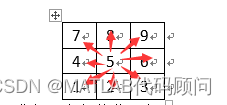
有了nearcell,那么就可以很简单的使用蚁群算法进行路径规划了,当然有可能走死胡同,这个就必须再设计一个回滚函数,走了死胡同就回滚。
部分MATLAB主程序如下:
clc;close all;clear all;warning off;%清除变量
rand('seed', 100);
randn('seed', 100);
format long g;xmin=0;
xmax=100;
ymin=0;
ymax=100;nx=10;% 划分数
ny=10;% 划分数
dx=(xmax-xmin)/nx;
dy=(ymax-ymin)/ny;
[nodetable,XY,nodnumber]=nodetabelfun(nx,ny,dx,dy);% 计算节点表格
XY(:,1)=XY(:,1)+xmin;
XY(:,2)=XY(:,2)+ymin;
gamma=0.2;
bocktable=bocktablefun(nodnumber,gamma);nodeset= find(bocktable==1);
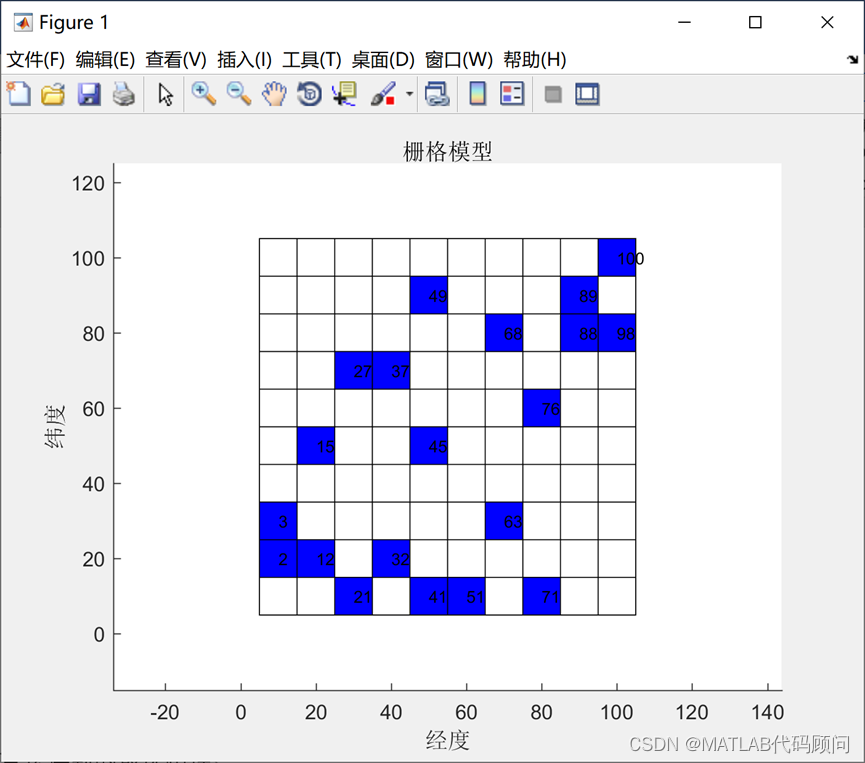
title1='栅格模型';
drawshelf(XY,dx,dy,nodeset,title1);% 绘图[neartable,E,G]=nearfun(nodetable,nodnumber,nx,ny,bocktable);% 计算节点邻接表格nodenumber=size(XY,1);
dmat=distancetable(XY,E);
startnodeID=1;% 起点
targetnodeID=20;% 终点maxgen=50;% 迭代次数
popsize=10; % 蚂蚁数量alpha=2; % 信息素重要程度因子
beta=3; % 启发函数重要程度因子
rho=0.1; % 信息素挥发因子
Q=1;tic;
Eta=0.01*ones(nodenumber,nodenumber);
tocL=length(targetnodeID);
Ttable02=topo_table(E);tracemat=zeros(maxgen,2);
Tau = ones(nodenumber,nodenumber); % 信息素矩阵初始化
gen = 1; % 迭代次数初值tic;
wait_hand = waitbar(0,'running...', 'tag', 'TMWWaitbar');
while gen<=maxgen% 多次循环ACOChrom=zeros(popsize,nodenumber);for i=1:popsize% 每个蚂蚁循环Ttable01=Ttable02;route=startnodeID;state=1;number_dem=targetnodeID;while state~=0curr_node=route(end);curr_topolopy=Ttable01(curr_node).topolopy;n=length(route);for k=1:nendP=P/sum(P);Pc=cumsum(P);target_index=find(Pc >= rand);next_node=curr_topolopy(target_index(1));route=[route next_node];else[state,route,Ttable01]=getroutefun(route,Ttable01,state,curr_node);endif route(end)==number_demstate=0;endendL1=length(route);ACOChrom(i,1:L1)=route;endcost= decodingFun(ACOChrom,popsize,dmat);% 计算目标函数[costu,inputps]=mapminmax(cost',100,200);costu=costu';% 记录结果[v1,index1]=min(cost);if gen==1bestlong001=v1;bestroute=ACOChrom(index1,:);endif bestlong001>v1;bestlong001=v1;bestroute=ACOChrom(index1,:);endtracemat(gen,1)=bestlong001;tracemat(gen,2)=mean(cost);Tau=updatetaufun(rho,Q,nodenumber,popsize,ACOChrom,costu,Tau);% 更新信息素gen=gen+1;waitbar(gen/maxgen,wait_hand);
end
delete(wait_hand);
toc% 输出结果
disp('蚁群算法得到的最优路径');
bestroute=bestroute(bestroute>0)% 绘图
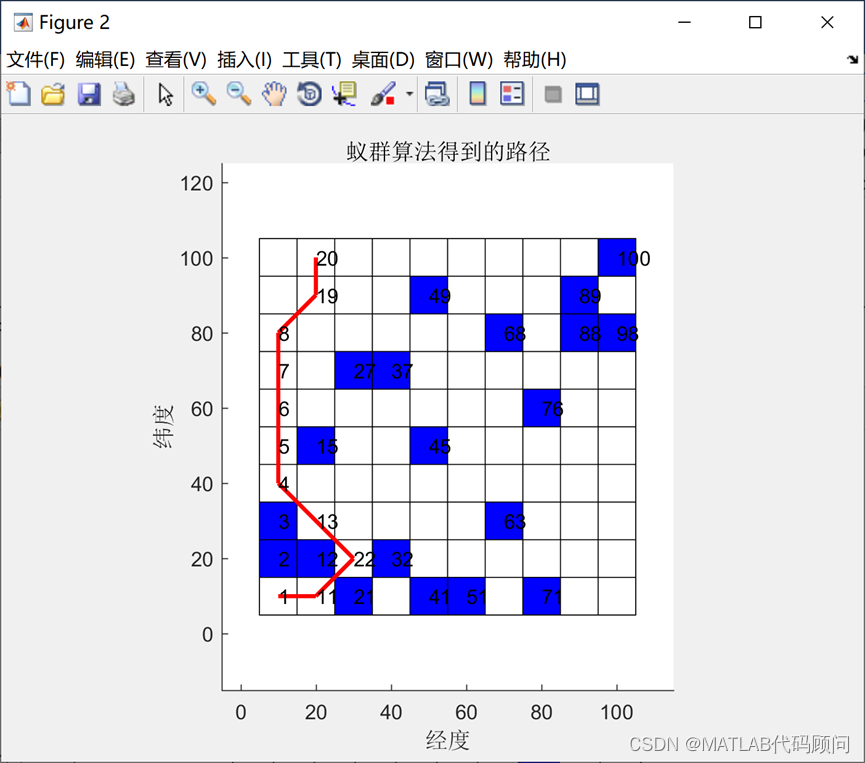
title1='蚁群算法得到的路径';
startnodeID=bestroute;
drawshelf2(XY,dx,dy,nodeset,startnodeID,title1)figure;
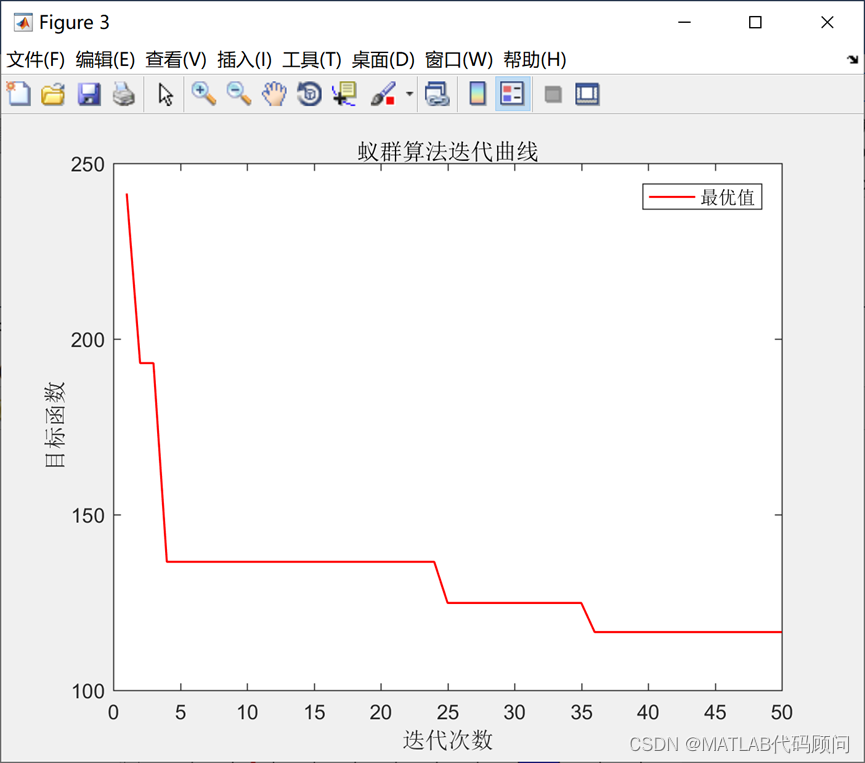
plot(tracemat(:,1),'r-','linewidth',1);
legend({'最优值'},'fontname','宋体');
xlabel('迭代次数','fontname','宋体');
ylabel('目标函数','fontname','宋体');
title('蚁群算法迭代曲线','fontname','宋体');程序结果:
时间已过 0.000757 秒。
时间已过 3.196282 秒。
蚁群算法得到的最优路径
bestroute =
1 11 22 13 4 5 6 7 8 19 20
>>










![【YOLOv8改进[Head检测头]】YOLOv8换个RT-DETR head助力模型更优秀](https://img-blog.csdnimg.cn/direct/0be32b831d7d42f9b2bf0c7e79706222.png)