【ollama】（5）：在本地使用docker-compose启动ollama镜像，修改模型存储位置，并下载qwen-0.5b模型，速度飞快

1，ollama项目

Ollama 是一个强大的框架，设计用于在 Docker 容器中部署 LLM。Ollama 的主要功能是在 Docker 容器内部署和管理 LLM 的促进者，它使该过程变得非常简单。它帮助用户快速在本地运行大模型，通过简单的安装指令，可以让用户执行一条命令就在本地运行开源大型语言模型，例如 Llama 2。

https://ollama.com/

https://www.bilibili.com/video/BV1HC411Y7P1/?vd_source=4b290247452adda4e56d84b659b0c8a2

【ollama】（5）：在本地使用docker-compose启动ollama镜像，并下载qwen-0.5b模型，速度飞快

2，整个docker-compose 配置如下：

version: '3.5'services:##################### 使用ollama部署大模型 ###################### OLLAMA_HOST       The host:port to bind to (default "127.0.0.1:11434")
# OLLAMA_ORIGINS    A comma separated list of allowed origins.
# OLLAMA_MODELS     The path to the models directory (default is "~/.ollama/models")ollama:restart: alwayscontainer_name: ollamaimage: ollama/ollamaports:- 8000:8000environment:- OLLAMA_HOST=0.0.0.0:8000- OLLAMA_MODELS=/data/modelsvolumes:- ./models/:/data/models# 命令启动 servecommand: serve

启动docker镜像服务：

docker-compose  up -d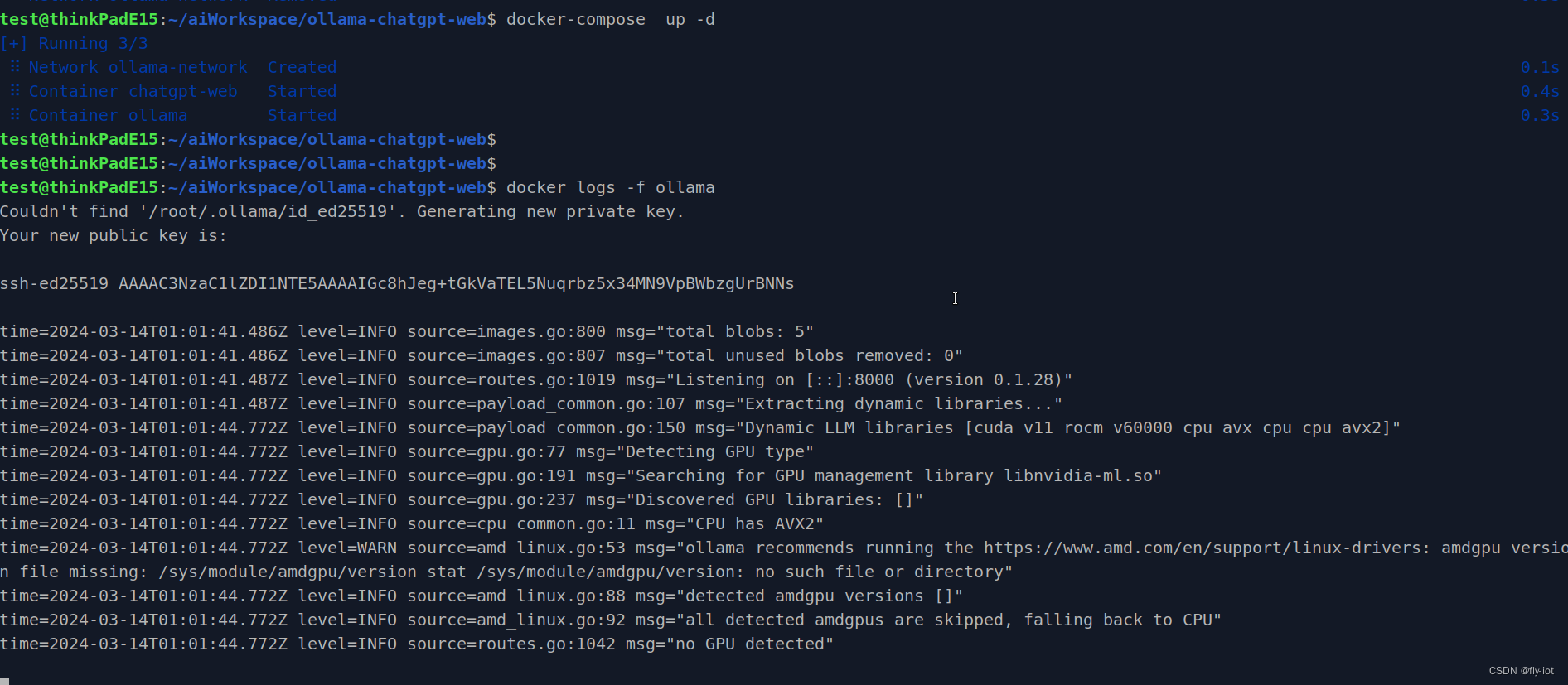

在这里插入图片描述

然后就可以执行命令测试了：

curl http://localhost:8000/v1/chat/completions \-H "Content-Type: application/json" \-d '{"model": "qwen:0.5b","stream":true,"messages": [{"role": "user","content": "你好"}]}'

$ curl http://localhost:8000/v1/chat/completions \-H "Content-Type: application/json" \-d '{"model": "qwen:0.5b","stream":true,"messages": [{"role": "user","content": "你好"}]}'
data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"你好"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"，"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"很高兴"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"为您"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"服务"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"。"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"有什么"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"我可以"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"帮助"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"您的"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"吗"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377122,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"？"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377123,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":"\n"},"finish_reason":null}]}data: {"id":"chatcmpl-163","object":"chat.completion.chunk","created":1710377123,"model":"qwen:0.5b","system_fingerprint":"fp_ollama","choices":[{"index":0,"delta":{"role":"assistant","content":""},"finish_reason":"stop"}]}data: [DONE]