一、插值与拟合简介
在数学建模过程中,通常要处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式,针对此情况,很自然的想法就是,构造一个简单的函数作为要考察数据或复杂函数的近似。插值和拟合就可以解决这样的问题。
给定一组数据,需要确定满足特定要求的曲线,如果所求曲线通过所给定有限个数据点,这就是插值。有时由于给定的数据存在测量误差,往往具有一定的随机性。因而,要求曲线通过所有数据点不现实也不必要。如果不要求曲线通过所有数据点,而是要求它反映对象整体的变化态势,得到简单实用的近似函数,这就是曲线拟合。
插值和拟合都是根据组数据构造一个近似函数, 但由于近似的要求不同,二者在数学方法上是完全不同的。而面对个实际问题,究竞应该用插值还是拟合,有时容易确定,有时并不明显。
由于插值和拟合是一种手段,并无绝对的适用赛题,也并不算是一种模型,故本篇没有适用赛题、模型流程、流程解析部分。后面将重于使用,分别介绍插值和拟合的操作。
二、插值
1.一维插值
①基本概念
已知未知函数在n+1个互不相同的观测点x0<x1<...<xn处的函数值(或观测值):
yi = f(xi) , i = 0, 1, ..., n
寻求一个近似函数(即近似曲线)中φ(x) ,使之满足
φ(xi) = yi, i = 0, 1, ..., n
即求一条近似曲线φ(x),使其通过所有数据点(xi, yi) i = 0, 1, ..., n
对任意非观测点X(X ≠ xi, i = 0,1, ..., n),要估计该点的函数值f(X),就可以用φ(X)的值作为f(X)的近似估计值,即φ(X) ≈ f(X)。通常称此类建模问题为插值问题,而构造近似函数的方法就称为插值方法。
观测点xi(i = 0, 1, ..., n)称为插值节点,f(x)称为被插函数或原函数,φ(x)为插值函数,φ(xi) = yi称为插值条件,含xi(i = 0, 1, ..., n)的最小区间[a, b](a = min{xi}, b = max{xi})称为插值区间,X称为插值点,φ(X)为被插函数f(x)在X ∈ [a, b] 点处的插值。
这里对于多项式插值,拉格朗日插值、牛顿插值等方法理论部分不做介绍,有兴趣的同学自行查阅。
②函数使用
Ⅰinterp1函数
MATLAB中一维函数interp1的调用格式为
vq = interp1(x0, y0, xq, method, extrapolation)-
x0:已知的插值节点
-
y0:对应x0的函数值
-
xq:欲求函数值的节点坐标
-
vq:求得的节点xq处的函数值
-
method:指定插值的方法,默认为线性插值。其值常用的有:
| 'nearest' | 最近邻插值 |
| 'linear' | 线性插值 |
| 'spline' | 三次样条插值,函数是二次光滑的 |
| 'cubic' | 立方插值,函数是一次光滑的 |
MATLAB2020A不提倡使用函数interp1,建议使用函数griddedInterpolant。
ⅡgriddedInterpolant函数
函数griddedInterpolant适用于任意维数的插值。
一维插值的调用格式为
F = griddedInterpolant(x, v, method, extrapolation)计算对应的函数值的使用格式为
vq = F(xq)n维插值的调用格式为
F = griddedInterpolant(x1, x2,..., xn, v, method, extrapolation)计算对应的函数值的使用格式为
vq = F(xq1, xq2,..., xqn)Ⅲcsape三次样条插值函数
三次样条插值还可以使用函数ecsape,csape的返回值是pp形式。求插值点的函数值,调用函数fnval。
pp = csape(x0, y0)使用默认的边界条件,即拉格朗日边界条件。
pp = csape(x0, y0, conds, valconds)中的conds指定插值的边界条件,详细见官网
利用pp结构的返回值,还可以计算返回值函数的导数和积分,命令分别为fnder,fnint,这两个函数的返回值还是pp结构。
| 调用格式 | 函数功能 |
| pp1 = csape(x0, y0) | 计算插值函数 |
| pp2 = fnder(pp1) | 计算pp1对应函数的导数,返回值pp2也是pp结构 |
| pp3 = fnint(pp1) | 计算pp1对应函数的积分,返回值pp3也是pp结构 |
| y = fnval(pp1, x) | 计算pp1对应的函数在x点的取值 |
2.二维插值
①基本概念
二维插值的基本概念和一维差不多,只不过曲线变成了曲面而已,不做赘述。
②网格数据的插值
已知m×n个节点(xi, yi, zij)(i = 1, 2,.., m; j = 1, 2, ..., n),且x1 <...< xm; y1 < ...< yn。求点(x, y)处的插值z。
Ⅰinterp2函数
z = interp2(x0, y0, z0, x, y, 'method')-
x0,y0:m维和n维向量,表示插值节点
-
z0:n×m矩阵,表示对应插值节点函数值
-
x,y:一维数组,表示插值点。x与y应是方向不同的向量,即一个是行向量,另一个是列向量
-
z:矩阵,行数为y的维数,列数为x的维数,表示得到的插值
-
method:用法同上面的一维插值
如果是三次样条插值,可以使用函数griddedInterpolant和csape。函数girddedInterpolant前面已经介绍过。
Ⅱcsape函数
pp = csape({x0, y0}, z0, conds, valconds);
z = fnval(pp, {x, y})-
x0,y0:分别为m维和n维向量
-
z0:m×n矩阵
-
z:矩阵,行数为y的维数,列数为x的维数,表示得到的插值
③散乱数据的插值
已知n个插值节点(xi, yi, zi)(i =1, 2, ..., n),求点(x, y)处的插值z。
Ⅰgriddata函数
函数griddata的调用格式为
ZI = griddata(x, y, z, XI, YI)-
x,y,z:均为n维向量,指明所给数据点的横坐标、纵坐标和竖坐标
-
XI,YI:给定的网格点的横坐标和纵坐标
-
ZI:网格(XI, YI)处的函数值。XI与YI应是方向不同的向量,即一个是行向量,另一个是列向量
ⅡscatteredInterpolant函数
函数scatteredInterpolant的调用格式为
Fz = scatteredInterpolant(x0, y0, z0, Method, ExtrapolationMethod);-
返回值Fz是结构数组,相当于给出了插值函数的表达式
- x0,y0,z0:分别为已知n个点的x,y,z坐标
- Method:插值方法
- ExtrapolationMethod:区域外部节点的外插方法
要计算插值点(x, y)处的值,调用Fz即可
z = Fz(x, y);三、拟合
1.线性最小二乘法
①解线性方程组拟合参数
要拟合等式中的参数a1, a2, ..., am,把观测值代入等式,得到线性方程组
RA = Y
则A = pinv(R) * Y或简化格式A = R \ Y
②约束线性最小二乘解
在最小二乘意义下解约束线性方程组
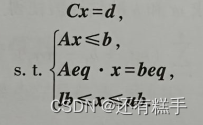
即求解数学规划问题
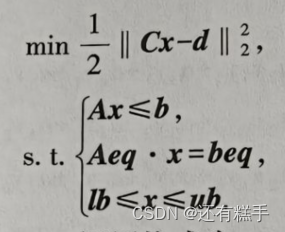
求解上述问题调用函数lsqlin
x = lsqlin(C, d, A, b, Aeq, beq, lb, ub);③多项式拟合
多项式拟合的函数为polyfit,调用格式为
p = polyfit(x, y, n) % 拟合n次多项式,返回值p是多项式对应的系数,排列次序为从高次幂系数到低次幂系数计算多项式p在x处的函数值
y = polyval(p, x);2.fittype和fit函数
函数fit需要和函数fittype配合使用,fittype用于定义拟合的函数类,fit进行函数拟合。fit既可以拟合一元或二元线性函数,也可以拟合一元或二元非线性函数。 这里介绍这两个函数的调用格式。
fittype的调用格式为
aFittype = fittype(libraryModeName) % 利用库模型定义函数类
aFittype = fittype(expression, Name, Value) % 利用字符串定义函数类
aFittype = fittype(linearModeTerm, Name, Value) % 利用基函数的线性组合定义函数类
aFittype = fittype(anonymousFunction, Name, Value) % 利用匿名函数定义函数类函数fit的调用格式为
fitobject = fit(x, y, aFittype) % x和y分别为自变量和因变量的观测值列向量,返回值fitobject为拟合函数的信息
fitobject = fit([x, y], z, aFittype) % [x, y]为自变量的观测值的两列矩阵,z为因变量的观测值列向量,这里是拟合二元函数
[fitobject, gof] = fit(x, y, aFittype, Name, Value) % 返回值gof为结构数组,给出了模型的一些检验统计量3.非线性拟合
MATLAB非线性拟合的主要函数有fit和lsqcurvefit,fit函数使用很方便,但只能拟合一元和二元函数,lsqcurvefit可以拟合任意多个自变量的函数,并且可以约束未知参数的上界和下界,下面用例子讲解。
①fit函数
用下表数据拟合函数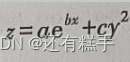
| x1 | 6 | 2 | 6 | 7 | 4 | 2 | 5 | 9 |
| x2 | 4 | 9 | 5 | 3 | 8 | 5 | 8 | 2 |
| y | 14.2077 | 39.3622 | 17.8077 | 11.8310 | 32.8618 | 16.9622 | 33.0941 | 11.1737 |
xy0 = d([1, 2], :)';
z0 = d(3, :)';
g = fittype('a * exp(b * x) + C*y^2', 'dependent' ,'z' , 'independent', {'x', 'y'});
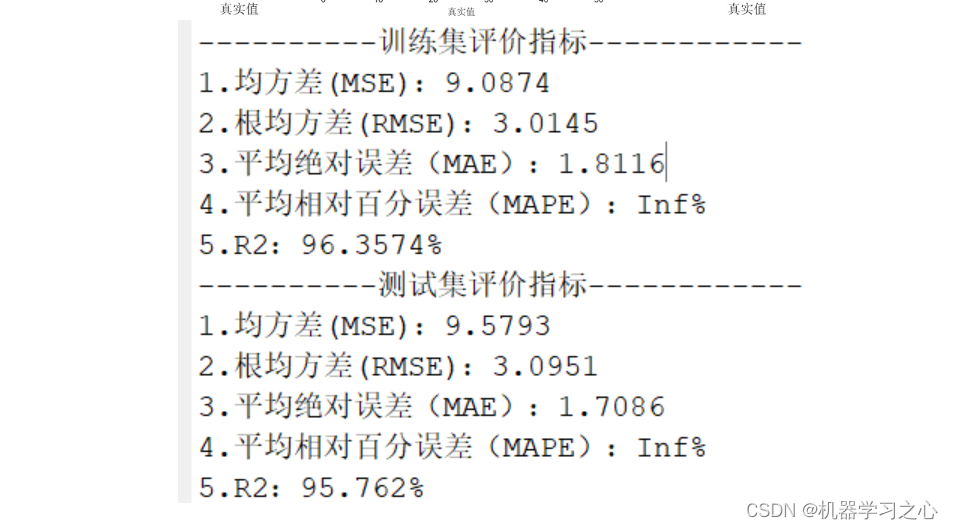
[f, st] = fit(xy0, z0, g, 'StartPoint', rand(1,3));求得z=6.193e的0.04353x次方+0.3995y²
拟合优度R² = 0.9995,拟合的剩余标准差RMSE = 0.2970,拟合效果很好。
②lsqcurvefit函数
要拟合函数y = f(θ, x),给定x的观测值xdata,y的观测值ydata,求参数向量θ,使得误差平方和最小。
lsqcurvefit函数的调用格式为
theta = lsqcurvefit(fun, theta0, xdata, ydata, lb, ub, options)- fun:定义函数f(θ, x)的M函数或匿名函数
- thata0:θ初始值
- lb,ub:参数θ的下界和上界
- options:设置计算过程的一些算法
- theta:拟合参数θ的值
本篇只是很浅显地介绍了各个函数,每个函数的具体用法和参数设置有兴趣的同学可以到官网查询。如果对其中原理理论部分感兴趣也可以查文献搜索。