目录
H数三角形(hard)
题目大意:
思路解析:
编辑
代码实现:
H数三角形(hard)
题目大意:

思路解析:

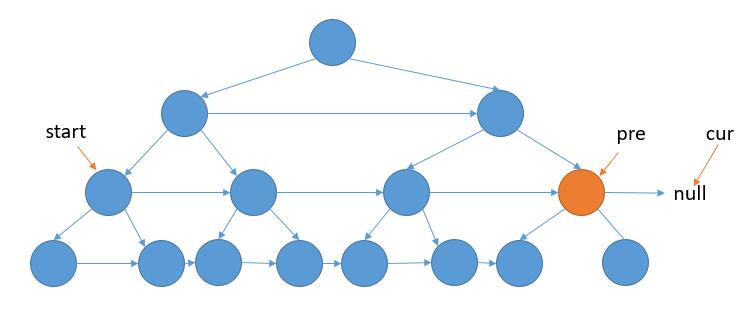
通过这张图可以发现,左腰和右腰是对称的,那么只要对于 (i,j)这个点,如果有一个端点能通过左腰和右腰能够到达这个点那么他就能组成一个数字三角形,但是我们如果遍历找是否有这样的点时间复杂度就会变为N^3, (数字三角形要求整个底面是连续的,所以我们在连续底面统计每一个点能通过左腰和右腰达到最右边的点(这里统计可以用树状数组维护))我们统计这个点通过右腰和左腰能到达最左的点,那么这个区间之内就是合法的数字三角形。

代码实现:
import java.io.*;
import java.util.*;public class Main {static int mod = (int) 1e9 + 7;static int mod9 = 998244353;static int N = 3003;static int[] tr;static Vector<Integer> g[];static int[][] d1; // 左腰static int[][] d2; // 右腰static int n;static int m;static long ans = 0;public static void main(String[] args) throws IOException {n = input.nextInt();m = input.nextInt();tr = new int[N];char[][] map = new char[N][N];g = new Vector[N * 2];for (int i = 0; i < n * 2 + 6; i++) {g[i] = new Vector<>();}d1 = new int[N][N];d2 = new int[N][N];for (int i = 1; i <= n; i++) {char[] s = input.next().toCharArray();for (int j = 1; j <= m; j++) {map[i][j] = s[j - 1];if (map[i][j] == '*'){ans --;d1[i][j] = d1[i-1][j+1] + 1;d2[i][j] = d2[i-1][j-1] + 1;}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (map[i][j] != '*') continue;int k = j;while (k + 1<=m && map[i][k+1] == '*') k++;solve(i, j, k);j = k;}}out.println(ans);out.flush();out.close();br.close();}public static void add(int x, int val){for (; x <= m; x += x & -x) {tr[x] += val;}}public static int sum(int x){if (x <= 0) return 0;int res = 0;for (; x > 0; x -= x &-x) res+=tr[x];return res;}public static void solve(int row, int left, int right){int mx = 0;int i;for (i = left; i <= right ; i+=2) {int L = i;int R = L + d1[row][i] * 2 - 2;mx = Math.max(mx, R);g[R].add(i);add(i, 1);R = i;L = R - d2[row][i] * 2 + 2;ans += sum(i) - sum(L - 1);for (Integer integer : g[i]) {add(integer, -1);}g[i].clear();}for (; i <= mx; i+=2) {for (Integer integer : g[i]) {add(integer, -1);}g[i].clear();}mx = 0;for (i = left + 1; i<=right; i+=2) {int L = i;int R = L + d1[row][i] * 2 - 2;mx = Math.max(mx, R);g[R].add(i);add(i, 1);R = i;L = R - 2 * d2[row][i] + 2;ans += sum(i) - sum(L - 1);for (Integer integer :g[i]) {add(integer,-1);}g[i].clear();}for(; i<=mx;i+=2){for (Integer integer :g[i]) {add(integer,-1);}g[i].clear();}}// -------------------------------- 模板 ---------------------------public static long gcd(long a, long b) {if (a == 0) return b;if (b == 0) return a;return gcd(b, a % b);}public static int gcd(int a, int b) {if (a == 0) return b;if (b == 0) return a;return gcd(b, a % b);}public static long pow(long a, long b, long mod) {long res = 1;while (b > 0) {if ((b & 1) == 1) res = (res * a) % mod;a = (a * a) % mod;b >>= 1;}return res;}//static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static Input input = new Input(System.in);static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static class Input {public BufferedReader reader;public StringTokenizer tokenizer;public Input(InputStream stream) {reader = new BufferedReader(new InputStreamReader(stream), 32768);tokenizer = null;}public String next() {while (tokenizer == null || !tokenizer.hasMoreTokens()) {try {tokenizer = new StringTokenizer(reader.readLine());} catch (IOException e) {throw new RuntimeException(e);}}return tokenizer.nextToken();}public int nextInt() {return Integer.parseInt(next());}}}