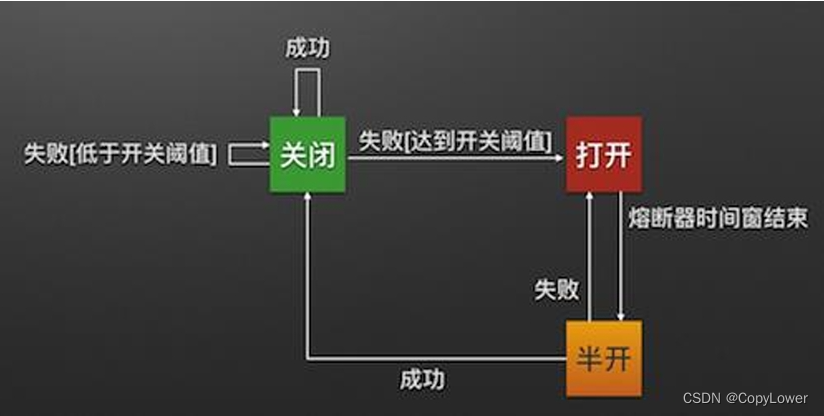
给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {int val;Node *left;Node *right;Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

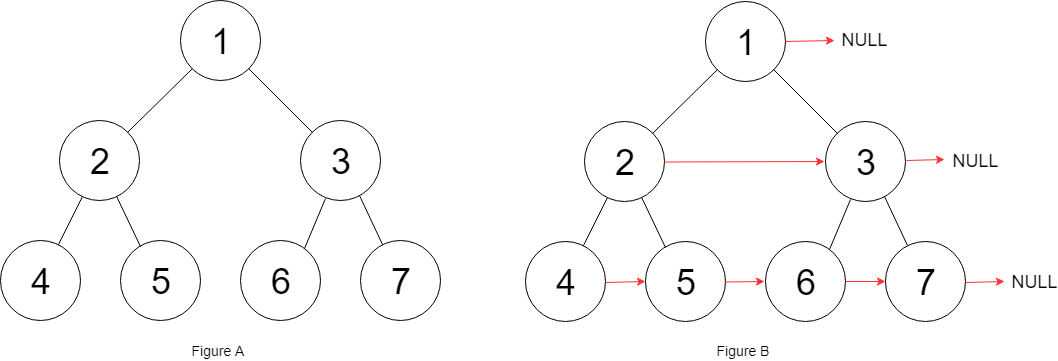
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

解法一 BFS

如果没有要求空间复杂度这道题就简单多了，我们只需要用一个队列做BFS，BFS参见 102 题。然后按顺序将每个节点连起来就可以了。

public Node connect(Node root) {if (root == null) {return root;}Queue<Node> queue = new LinkedList<Node>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();Node pre = null;for (int i = 0; i < size; i++) {Node cur = queue.poll();//从第二个节点开始，将前一个节点的 pre 指向当前节点if (i > 0) {pre.next = cur;}pre = cur;if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}}return root;
}

解法二 迭代

当然既然题目要求了空间复杂度，那么我们来考虑下不用队列该怎么处理。只需要解决三个问题就够了。

• 每一层怎么遍历？

  之前是用队列将下一层的节点保存了起来。

  这里的话，其实只需要提前把下一层的next构造完成，到了下一层的时候就可以遍历了。

• 什么时候进入下一层？

  之前是得到当前队列的元素个数，然后遍历那么多次。

  这里的话，注意到最右边的节点的next为null，所以可以判断当前遍历的节点是不是null。

• 怎么得到每层开头节点？

  之前队列把当前层的所以节点存了起来，得到开头节点当然很容易。

  这里的话，我们额外需要一个变量把它存起来。

三个问题都解决了，就可以写代码了。利用三个指针，start 指向每层的开始节点，cur指向当前遍历的节点，pre指向当前遍历的节点的前一个节点。

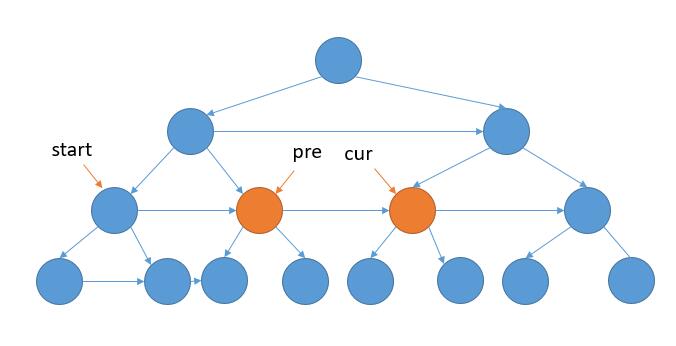
如上图，我们需要把 pre 的左孩子的 next 指向右孩子，pre 的右孩子的next指向cur的左孩子。

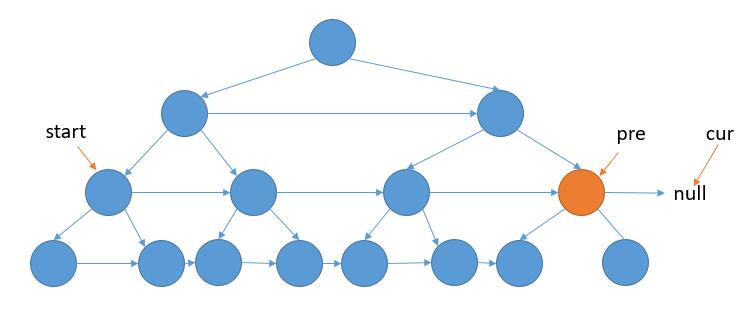
如上图，当 cur 指向 null 以后，我们只需要把 pre 的左孩子的 next 指向右孩子。

public Node connect(Node root) {if (root == null) {return root;}Node pre = root;Node cur = null;Node start = pre;while (pre.left != null) {//遍历到了最右边的节点，要将 pre 和 cur 更新到下一层，并且用 start 记录if (cur == null) {//我们只需要把 pre 的左孩子的 next 指向右孩子。pre.left.next = pre.right;pre = start.left;cur = start.right;start = pre;//将下一层的 next 连起来，同时 pre、next 后移} else {//把 pre 的左孩子的 next 指向右孩子pre.left.next = pre.right;//pre 的右孩子的 next 指向 cur 的左孩子。pre.right.next = cur.left;pre = pre.next;cur = cur.next;}}return root;
}

分享下 leetcode 的高票回答的代码，看起来更简洁一些，C++ 写的。

void connect(TreeLinkNode *root) {if (root == NULL) return;TreeLinkNode *pre = root;TreeLinkNode *cur = NULL;while(pre->left) {cur = pre;while(cur) {cur->left->next = cur->right;if(cur->next) cur->right->next = cur->next->left;cur = cur->next;}pre = pre->left;}
}

我的代码里的变量和他的变量对应关系如下。

我的 start    pre    cur|       |      |
他的  pre     cur    cur.next

除了变量名不一样，算法本质还是一样的。