目录
1.课题概述
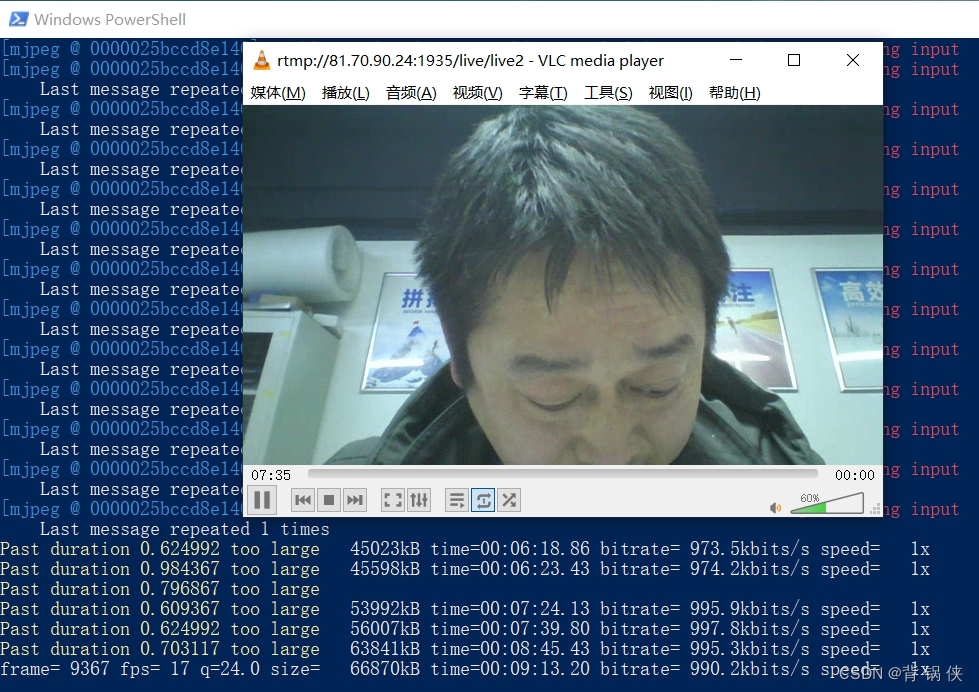
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
5.完整工程文件
1.课题概述
基于PID-bang-bang控制算法的卫星姿态控制。仿真输出控制器的控制收敛曲线,卫星姿态调整过程的动画。
2.系统仿真结果
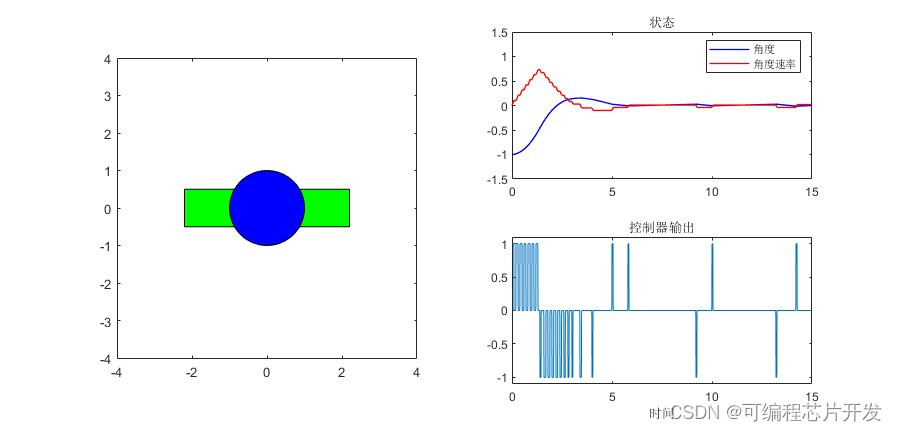
3.核心程序与模型
版本:MATLAB2022a
...........................................................%动画绘制部分if mod(t(i),3/Fcycle) < Tglobal % 每隔一段时间绘制一次图形(降低绘图频率以提高效率) % 计算卫星位置[x_sat, y_sat] = func_satellite(x(1,i),Len1,Len2); % 计算推力向量位置[x1_th,y1_th,x2_th,y2_th] = func_thrust(u(i),x(1,i),Len1,Len2,Len3,Len4); figure(1); % 创建或激活图形窗口1 subplot(2,2,[1,3]); % 在2x2的子图布局中选择第1和第3个位置进行绘图 fill(x_sat,y_sat,'g'); % 绘制卫星位置(绿色填充) hold on; % 保持当前图形,以便在同一张图上绘制更多内容 fill(r*cos(0:.1:2*pi),r*sin(0:.1:2*pi),'b'); % 绘制一个蓝色的圆(可能是表示卫星轨迹或参考圆) fill(x1_th,y1_th,'r'); % 绘制推力向量的起点(红色填充) fill(x2_th,y2_th,'r'); % 绘制推力向量的终点(红色填充) hold off; % 释放当前图形,不再在同一张图上绘制更多内容 pbaspect([1 1 1]); % 设置绘图区域的宽高比和深度比为1:1:1,确保图形不会变形 axis([-4 4 -4 4]); % 设置坐标轴范围 subplot(2,2,2); % 在2x2的子图布局中选择第2个位置进行绘图 plot(t(1:i),x(1,1:i),'-b',... % 绘制角度随时间变化的曲线(蓝色实线) 'LineWidth',1,... % 设置线宽为1 'MarkerSize',6,... % 设置标记点大小为6 'MarkerEdgeColor','k',... % 设置标记点边缘颜色为黑色 'MarkerFaceColor',[0.9,0.0,0.0]); % 设置标记点填充颜色为红色(但这里实际上并不会显示标记点,因为plot函数没有添加标记点的选项) hold on; % 保持当前图形,以便在同一张图上绘制更多内容 plot(t(1:i),x(2,1:i),'-r',... % 绘制角度速率随时间变化的曲线(红色实线)(注意:这里应该使用新的变量或不同的线型来区分两条曲线) 'LineWidth',1,... % 设置线宽为1(与上一条曲线相同,可能会覆盖) 'MarkerSize',6,... % 设置标记点大小为6(同上) 'MarkerEdgeColor','k',... % 设置标记点边缘颜色为黑色(同上) 'MarkerFaceColor',[0.9,0.9,0.0]); % 设置标记点填充颜色为黄色(同上)(但这里实际上并不会显示标记点) title('状态'); % 设置子图标题为“状态” legend('角度','角度速率'); % 添加图例,说明两条曲线分别代表什么 xlim([0 SimuTime]); % 设置x轴范围(时间范围) ylim([-1.5 1.5]); % 设置y轴范围(角度和角度速率范围)(注意:这个范围可能不适合角度速率的显示) subplot(2,2,4); % 在2x2的子图布局中选择第4个位置进行绘图(但实际上这里应该是第3个位置,因为上面只用了两个位置) plot(t(1:i),u(1:i)); % 绘制控制器输出随时间变化的曲线 title('控制器输出'); % 设置子图标题为“控制器输出” xlim([0 SimuTime]); % 设置x轴范围(时间范围) ylim([-1.1 1.1]); % 设置y轴范围(控制器输出范围) xlabel('时间'); % 设置x轴标签为“时间” end % 积分累积(注意:这里可能有一个逻辑错误,因为每次循环都在累积误差,但没有在pwm更新时刻重置或调整累积值) Errsum = Errsum + Ref_pos - x(1,i); % 累积位置误差(但这里实际上是在累积位置误差的差值) % 状态传播(更新下一个时刻的状态) x(:,i+1) = x(:,i) + (Astate*x(:,i) + Bstate*u(i))/Fcycle; % 使用离散时间状态空间方程更新状态(但这里可能存在数组越界问题,因为当i=end时,x(:,i+1)会超出数组范围) i = i + 1; % 循环计数器加1(但这里实际上存在一个问题:当i=end时,上面的代码会导致数组越界错误) end
334.系统原理简介
PID(比例-积分-微分)控制器是一种广泛使用的控制算法,它通过计算误差信号的比例、积分和微分项来调整系统的输出,以减小误差并达到期望的控制目标。Bang-Bang控制则是一种简单的双模态控制策略,其中控制器输出在两个极值之间切换,通常用于实现快速响应。
在卫星姿态控制中,PID-Bang-Bang控制算法可能结合了两者的特点:当误差较大时,采用Bang-Bang控制以快速减小误差;当误差较小时,切换到PID控制以实现更精细的调整。在卫星姿态控制系统中,PID控制器(比例-积分-微分控制器)与bang-bang控制结合使用,能够有效克服单一控制策略的局限性,实现对卫星姿态的精确、快速调节。
-
PID控制器: 基于误差(e(t))进行工作,误差为期望姿态角(θ_d)与实际姿态角(θ)之差,即 e(t) = θ_d - θ。PID控制器输出(u(t))由以下三部分组成:
u(t) = K_p * e(t) + K_i * ∫e(t)dt + K_d * de(t)/dt
其中:
- K_p是比例增益,它直接影响系统对当前误差的响应速度。
- K_i是积分增益,用于消除稳态误差,防止误差累积。
- K_d是微分增益,通过预测未来误差变化趋势,提高系统的动态性能和稳定性。
-
Bang-Bang控制: Bang-Bang控制是一种开关型控制策略,其输出要么是最大值U_max,要么是最小值U_min,取决于当前误差是否超出设定的阈值。在卫星姿态控制中,当卫星姿态偏差超出预定范围时,bang-bang控制器会立即输出最大或最小控制力矩,以尽快纠正姿态。
-
PID-bang-bang混合控制: 在实际应用中,PID控制可提供连续且平滑的控制输出,但可能在某些极端条件下反应不足;而bang-bang控制虽然反应迅速,但易导致系统震荡。因此,将两者结合,通常会在正常状态下采用PID控制,而在姿态偏差过大、需要快速响应时切换至bang-bang控制。
综合以上,PID-bang-bang混合控制的具体实施可能是:当卫星姿态误差e(t)在一定范围内时,采用PID控制输出u_PID(t);当误差超出预设阈值时,则切换为bang-bang控制,输出u_BB(t)。这样既能保证姿态控制的稳定性和精确性,又能应对突发的大偏差情况,实现对卫星姿态的有效控制。
5.完整工程文件
v