---

一、嵌套调用的过程

def show1():print("show 1 run start")show2()print("show 1 run end")def show2():print("show 2 run start")show3()print("show 2 run end")def show3():print("show 3 run start")print("show 3 run end")show1()

执行结果

show 1 run start
show 2 run start
show 3 run start
show 3 run end
show 2 run end
show 1 run end

嵌套调用的过程图解

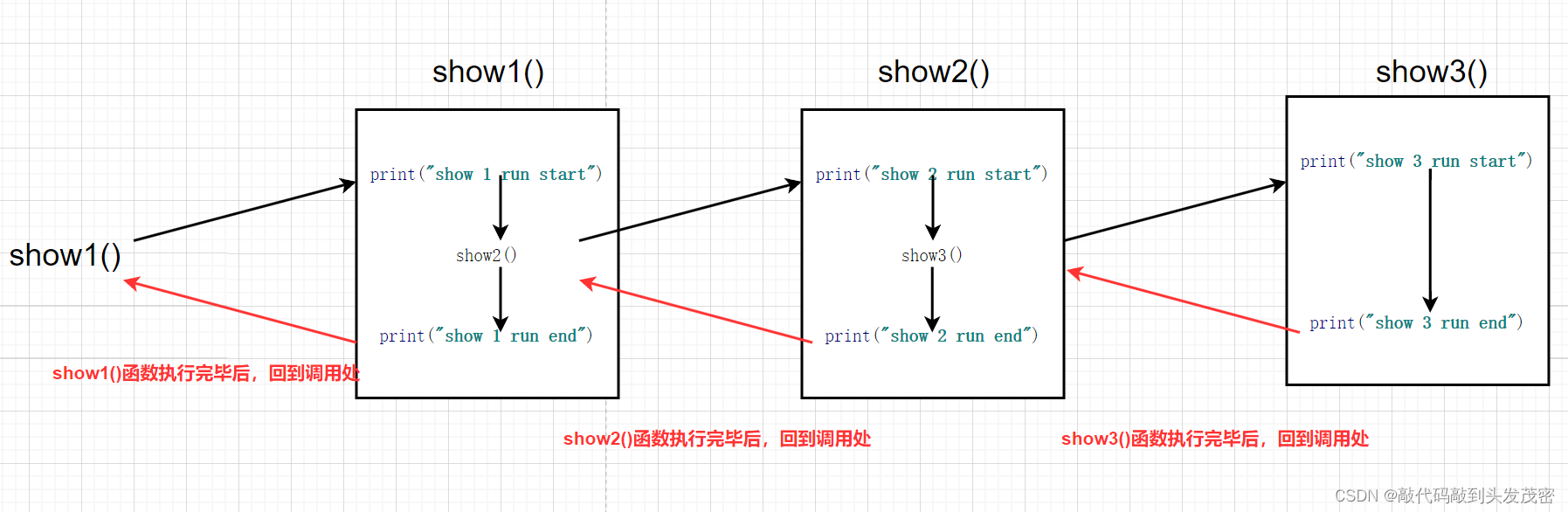
函数一旦执行结束，一会先回到调用处

二、递归的基本原则

1、递归的基本原则

递归函数通常遵循以下原则：

• 定义基本情况:确定一个或多个输入的特殊情况，当满足这些条件时，递归函数将直接返回结果而不再调用自身。
• 减小问题规模:通过调用自身来解决一个规模更小的问题，这样每次递归调用都在问题规模上取得了进展。也就是需要一个已定义好的规则来使其它非基本的情况转化为基本情况。
• 终止条件:递归函数必须包含能够导致函数不再递归调用的条件，以避免无限递归。

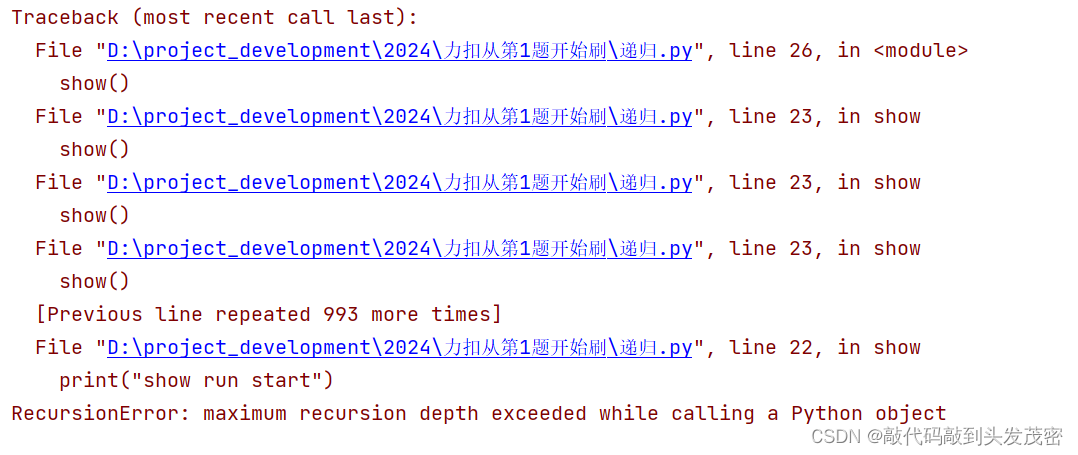
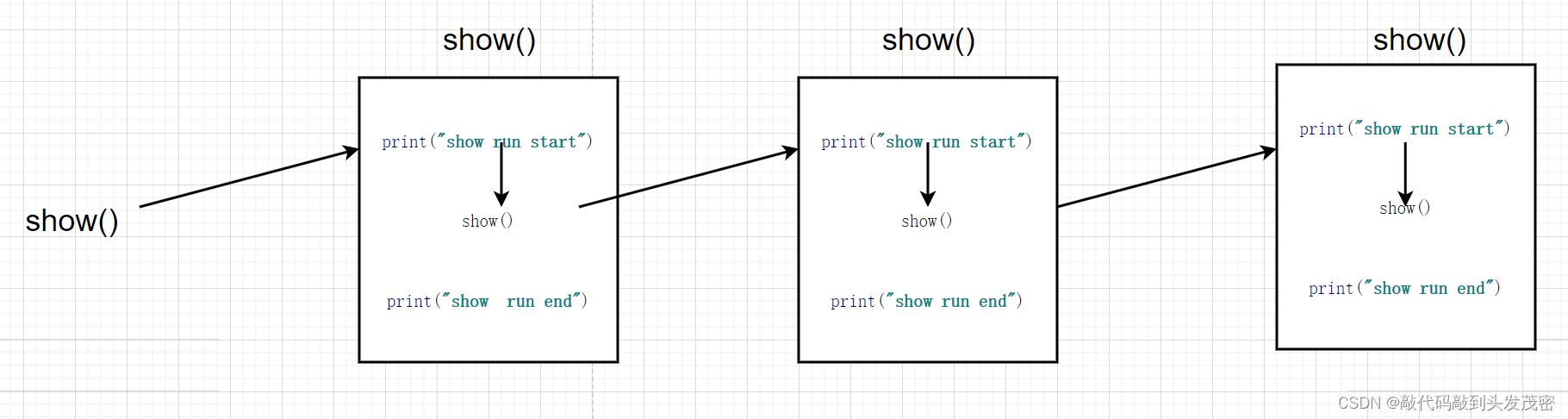
2、无限递归调用

def show():print("show run start")show()print("show run end")show()

无限递归调用报错
RecursionError: maximum recursion depth exceeded while calling a Python object

3、正常递归调用

def show(n):print(f"show run start-{n}")if n<10:show(n+1)print(f"show run end-{n}")show(1)

递归函数同嵌套函数调用一样：谁调用的你，返回到调用处

show run start-1
show run start-2
show run start-3
show run start-4
show run start-5
show run start-6
show run start-7
show run start-8
show run start-9
show run start-10
show run end-10
show run end-9
show run end-8
show run end-7
show run end-6
show run end-5
show run end-4
show run end-3
show run end-2
show run end-1进程已结束，退出代码为 0

当代码执行到24行时，先恢复show(9)的状态
show(9)是由show(8)的调用的，先恢复show(8)的状态
依次

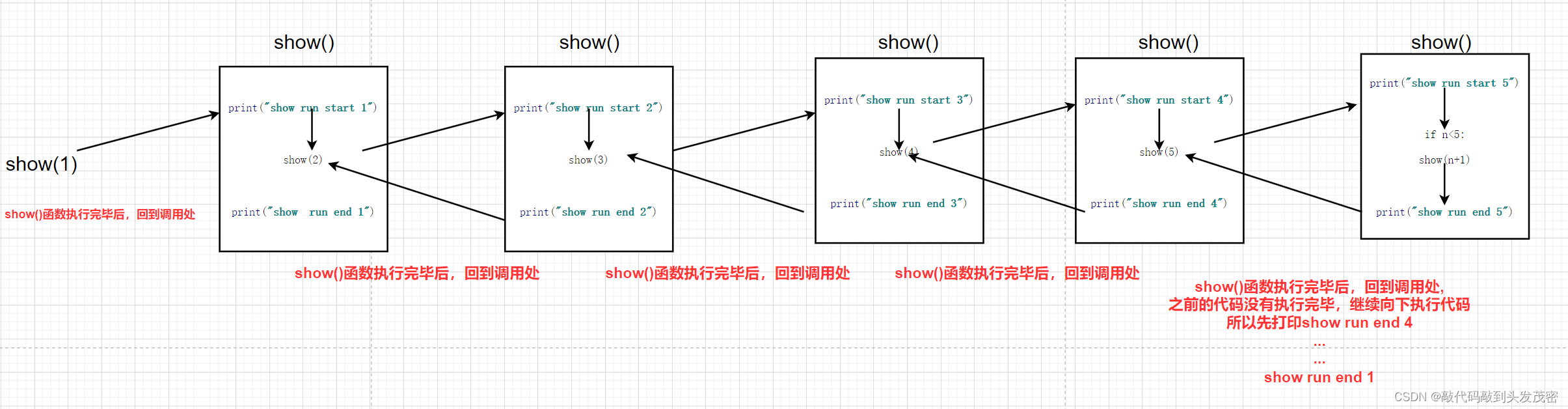
与嵌套函数调用过程相比：嵌套函数是由多个函数完成的，递归是有1个函数完成的

4、阶乘问题

def f(n):if n==0 or n==1:return 1return n*f(n-1)print(f(5))

执行流程：

5 * f(4)
5 * (4 * f(3))
5 * (4 * (3 * f(2)))
5 * (4 * (3 * 2 * f(1))))
5 * (4 * (3 * 2 * 1))
5 * (4 * (3 * 2))
5 * (4 * 6)
5 * 24
120

5、力扣：231. 2 的幂

简单

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。
如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

示例 1：
输入：n = 1
输出：true
解释：20 = 1

示例 2：
输入：n = 16
输出：true
解释：24 = 16

示例 3：
输入：n = 3
输出：false
示例 4：
输入：n = 4
输出：true

示例 5：
输入：n = 5
输出：false

class Solution:def isPowerOfTwo(self, n: int) -> bool:def panduan(s):if s <= 0:return Falseelif s == 1:return Trueelif s == 2:return Trueelse:if s % 2 == 0:return panduan(s // 2)else:return Falsereturn panduan(n)

6、力扣面试题 08.05. 递归乘法

中等

递归乘法。 写一个递归函数，不使用 * 运算符， 实现两个正整数的相乘。可以使用加号、减号、位移，但要吝啬一些。
示例1:
输入：A = 1, B = 10
输出：10

示例2:
输入：A = 3, B = 4
输出：12
提示:
保证乘法范围不会溢出

class Solution:def multiply(self, A: int, B: int) -> int:if B == 0:return 0return A + self.multiply(A, B - 1)r=Solution()
A=3
B=4
print(r.multiply(A, B))

执行流程

3+multiply(3, 3)
6+multiply(3, 2)
9+multiply(3, 1)
12+multiply(3, 0)

7、力扣、326. 3 的幂

简单

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

示例 1：
输入：n = 27
输出：true

示例 2：
输入：n = 0
输出：false

示例 3：
输入：n = 9
输出：true

示例 4：
输入：n = 45
输出：false

class Solution:def isPowerOfTwo(self, n: int) -> bool:def panduan(s):if s <= 0:return Falseelif s == 1:return Trueelif s % 3 != 0:return Falseelse:return panduan(s / 3)return panduan(n)r=Solution()
n=9
print(r.isPowerOfTwo(n))

8、力扣342. 4的幂

简单

给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4x

示例 1：
输入：n = 16
输出：true

示例 2：
输入：n = 5
输出：false

示例 3：
输入：n = 1
输出：true

class Solution:def isPowerOfTwo(self, n: int) -> bool:def panduan(s):if s <= 0:return Falseelif s == 1:return Trueelif s % 4 != 0:return Falseelse:return panduan(s // 4)return panduan(n)r=Solution()
n=1
print(r.isPowerOfTwo(n))