向量是线性代数中最为基础的概念。

何为向量？

        从物理上看， 向量就是既有大小又有方向的量，只要这两者一定，就可以在空间中随便移动。

        从计算机应用的角度看，向量和列表很接近，可以用来描述某对象的几个不同属性， 比如长2宽3，就可以写成。

        数学上给出最为广义的定义，一切对于相加和数乘有意义的都可以是向量。这实际上暗示了这两种运算会贯穿整个线性代数。

一种思考方式

        一种很好的思考向量的方式是：看到一个向量，想到一个箭头，它落在某个坐标系，且起点大多数时候固定在原点。

        这与上述的第一种定义契合，即“向量是空间中的箭头”。

        现在再看第二种定义，即“向量是有序的数字列表”：在定义了单位长度之后，我们就可以给出一个向量的坐标，这就是一个有序列表，它指示我们如何从向量的出发点（原点）到达向量的尖端。比如，告诉我们应该先沿着x轴负方向走2单位，再沿着y轴正方向走3个单位。

        每个有序列表对应唯一一个箭头，每个箭头对应唯一一个有序列表。

向量相加

        现在来考虑两种最基本运算中的加法。

        几何上看

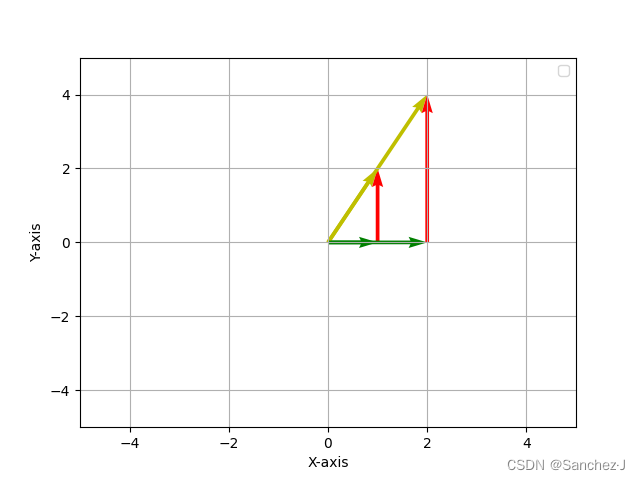
        沿用上述的思考方式，定义中的向量相加，就是把两个箭头首尾相接，然后画一个从前一个向量的首（原点）到后一个向量的尾的向量，这个向量就是结果。像这样

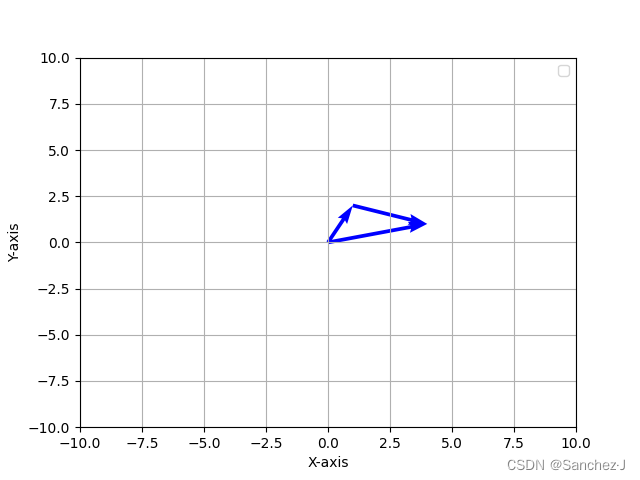
        但为什么要这样定义， 而不是从首到首呢？像这样

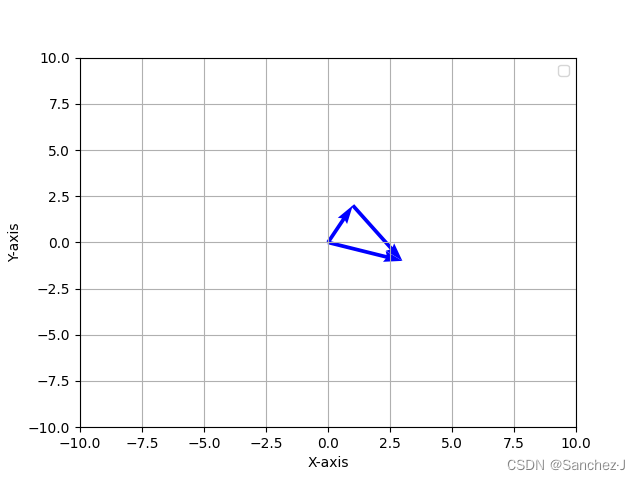
        因为往往将向量看作一个特定的运动，从首到尾， 按这种定义，向量的和就是先后沿着两个向量运动的整体上的结果，具有很直观的意义。

        实际上，如果把这种加法放到一维坐标系（数轴）上，其实就是在数轴上做数字加减的方法。

        代数上看

        第一个向量坐标是（1， 2）第二个向量坐标是（3， -1）。

        前面提到过，这个坐标指示我们如何通过先后沿平行x轴和y轴的方向移动，从一个向量的首走到尾，那么对于两个首位相接的向量，我们做加法的任务就是找出类似的这种方案，从第一个向量的首走到第二个向量的尾。

        在得到这个方案之前，我们只知道，先走第一个向量，再紧接着走第二个向量，按坐标给出的信息，这是一个4步的方案：x轴1，y轴2，x轴3，y轴-1。我们要得到的方案是两步的，也就是x轴几，y轴几。

        因为x轴和y轴上的行走是独立的，所以我们可以交换顺序，先做水平运动，再做竖直运动。整体上看，就等同于在x轴走（1+3）在y轴走（2-1）。这样我们就找到了我们要找的方案。

       

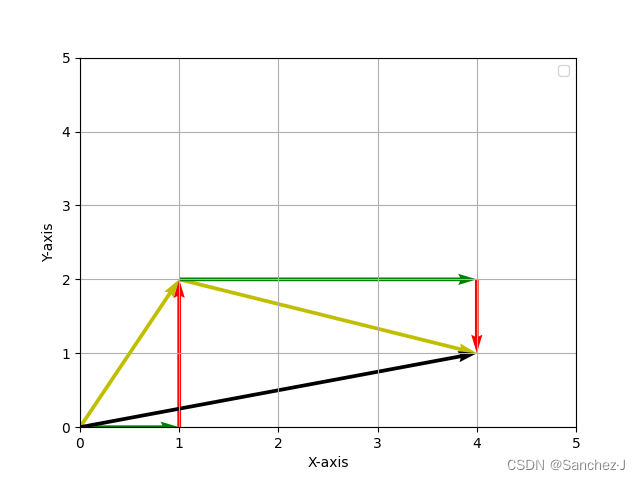
        这样我们也就推出了向量的加法法则，也知道了为什么要这样加。即有

向量数乘 

        对向量乘上一个数，本质上就是在做缩放（scaling）

        拉伸或压缩，如果有负号就反向。

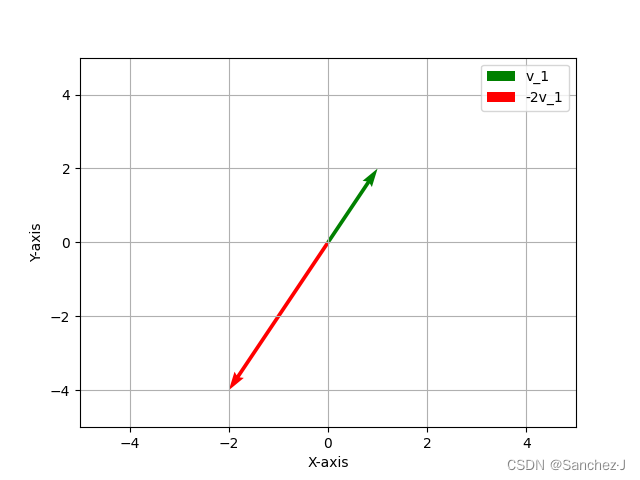
         这个用来缩放（scaling）的数，英文上很自然的可以叫做scalar，确实有这个词，而它的中文翻译是标量。所以标量其实就可以理解成用来缩放向量的东西。在线性代数中，标量的作用基本上就是用来缩放向量。

        数乘的运算法可以用相似推出来， 就是对每个分量分别乘上标量。

 

实际上，无论从哪个角度来看待向量都可，线性代数的效用很少仅仅体现在其中一个角度上，而是体现在这些不同角度的相互转化中。