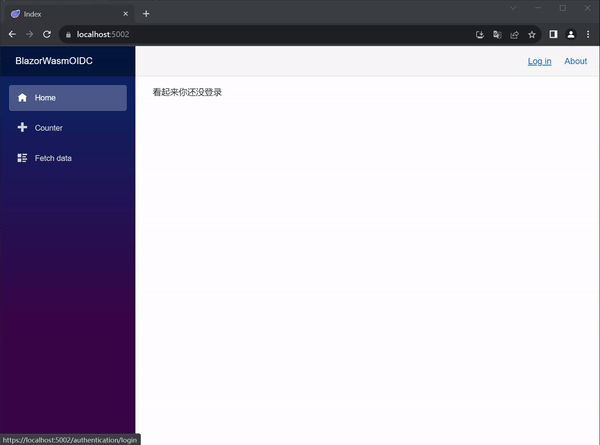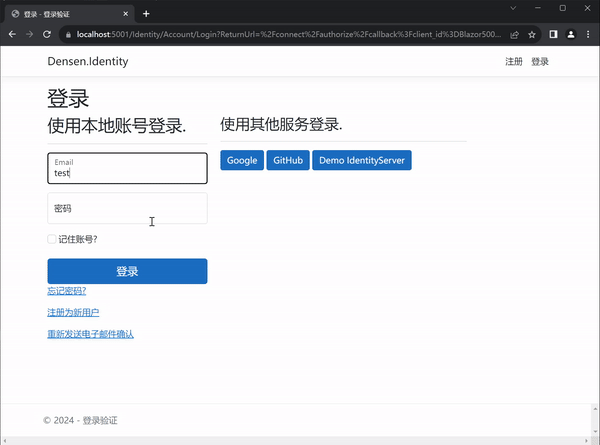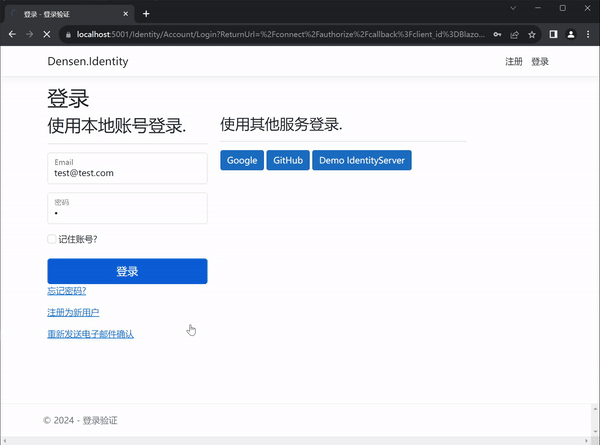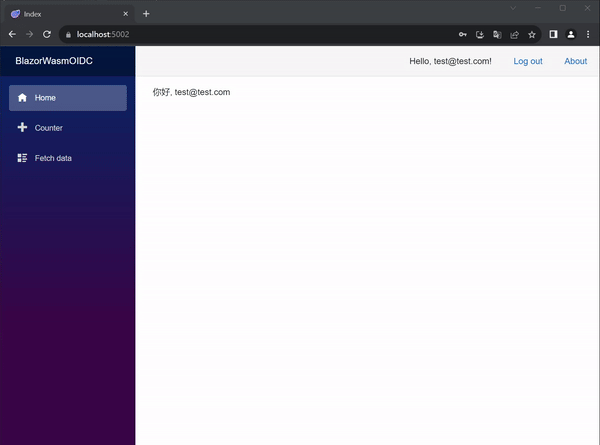
标准差(Standard Deviation)在科学领域引起了广泛的困惑,现在是将其从常用的统计方法中替换为平均偏差(one of mean deviation, 比如 MAD )的时候了。
原文链接:2014 : WHAT SCIENTIFIC IDEA IS READY FOR RETIREMENT?
标准差(STD)应该留给数学家、物理学家和数学统计学家推导极限定理。在计算机时代,使用标准差进行统计分析并没有科学依据,其缺点在社会科学等领域更为明显,因为人们往往不加选择地机械地应用它来解决问题。
假设有人刚刚要求您测量过去五天内您所在城镇的气温(或公司的股票价格,或您叔叔的血压)的“平均每日变化”。这五个变化是:(-23, 7, -3, 20, -1)。你会怎么做呢?
我们有两种方法:均方根偏差和 MAD。均方根偏差的计算结果为15.7,而MAD的结果为10.8,后者更接近实际情况(reality)。事实上,每当人们在获得标准差数后做出决定时,他们都会表现得这个值是平均偏差的期望(the expected mean deviation)。
这一切都源于一次历史偶然:1893 年,伟大的卡尔·皮尔逊 (Karl Pearson) 为所谓的“均方根误差” "root mean square error" 引入了“标准差” "standard deviation" 一词。混乱从那时开始:人们认为这意味着平均偏差。这个想法一直存在:每次报纸试图澄清市场“波动性”"volatility" 的概念时,虽然口头上定义为平均偏差,但给出的数值测量却是更高的标准差。
不仅是记者,我也注意到商务部和美联储的官方文件、甚至是市场波动性声明中的监管机构也存在这种混淆。更糟糕的是,我们发现许多数据科学家(包括许多拥有博士学位的)在实际中也会混淆两者。
这种混淆源于对非直观事物的错误术语。由于心理偏差,一些人会将 MAD 误认为 STD,因为前者更容易被想到。
MAD在样本测量中更准确、波动性更小,因为它自然加权,而标准差将观测值本身作为权重,对大的观测值赋予大的权重,从而过分强调尾部事件。
我们常在方程中使用 STD,但实际上经常在过程中将其转换为 MAD(例如在金融领域的期权定价)。在高斯世界中,STD约为MAD的1.25倍,即。但在随机波动性中,STD 常常高达 MAD 的1.6倍。
许多统计现象和过程有“无限方差”(如著名的帕累托80/20规则),但具有有限且非常规范的平均绝对偏差。只要存在平均值,就存在 MAD。反之(无限MAD 和有限 STD)则不成立。
许多经济学家因混淆而忽视了“无限方差”模型,以为这意味着“无限平均偏差”。五十年前,当伟大的本诺特·曼德尔布罗特提出他的无限方差模型时,经济学家因混淆而恐慌。
这样一个小问题导致了大量混淆:我们的科学工具远远领先于我们的日常直觉,这对科学而言开始成为一个问题。因此,我以罗纳德·A·费舍尔爵士的话作结:“统计学家不能逃避理解他所应用或推荐的流程的责任。”
社会和生物科学的概率问题不止这些:研究者使用罐头式的统计概念而不理解它们,滥用 "n of 1"、"n large", or "this is anecdotal" (for a large Black Swan style deviation),将 anecdotes 误为信息、信息误为 anecdotes 。事实上,大多数人在“声望很高”的期刊上使用回归分析,却不真正明白其含义及其所能(和不能)作出的声明。由于缺乏现实检验和风险投入,加之伪复杂性的外衣,社会科学家可能会在概率问题上犯下基本错误,却仍能在职业上蓬勃发展。
指北君续个狗尾
塔勒布写的很好,指北君尝试狗尾续貂补充一下。
塔勒布说的 one of mean deviation,一般是指 MAD。MAD 在实际中一般指平均绝对偏差(the mean absolute deviation),但在有时候有人也会用它来指代中值绝对偏差(the median absolute deviation)。这两个指标其实都是平均绝对偏差Average absolute deviation 中的一种,在下式中,只不过是选取了不同的 。
在机器学习中,和 STD 以及 MAD 相关的概念就是 RMSE (Root Mean Squared Error) 和 MAE (Mean Absolute Error) 了。逻辑和上面也是一样。比如对于有 Outliers 的数据来说,选取不同的优化目标,会得到不同的拟合。
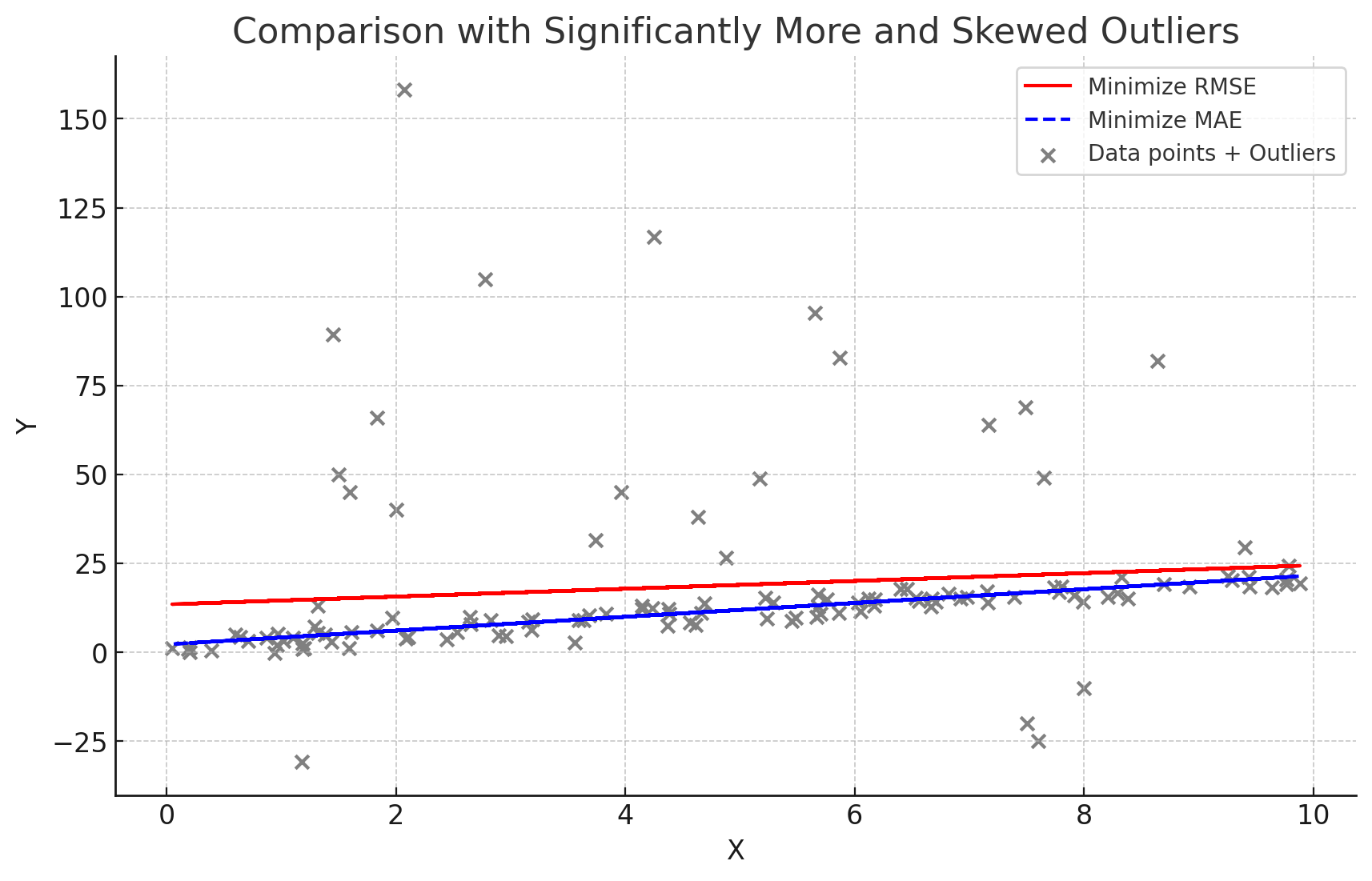
塔勒布说的这个原因也是各种量化模型中选取 MAE 为预测指标的一个原因。
本文由 mdnice 多平台发布