机器学习：特征工程笔记

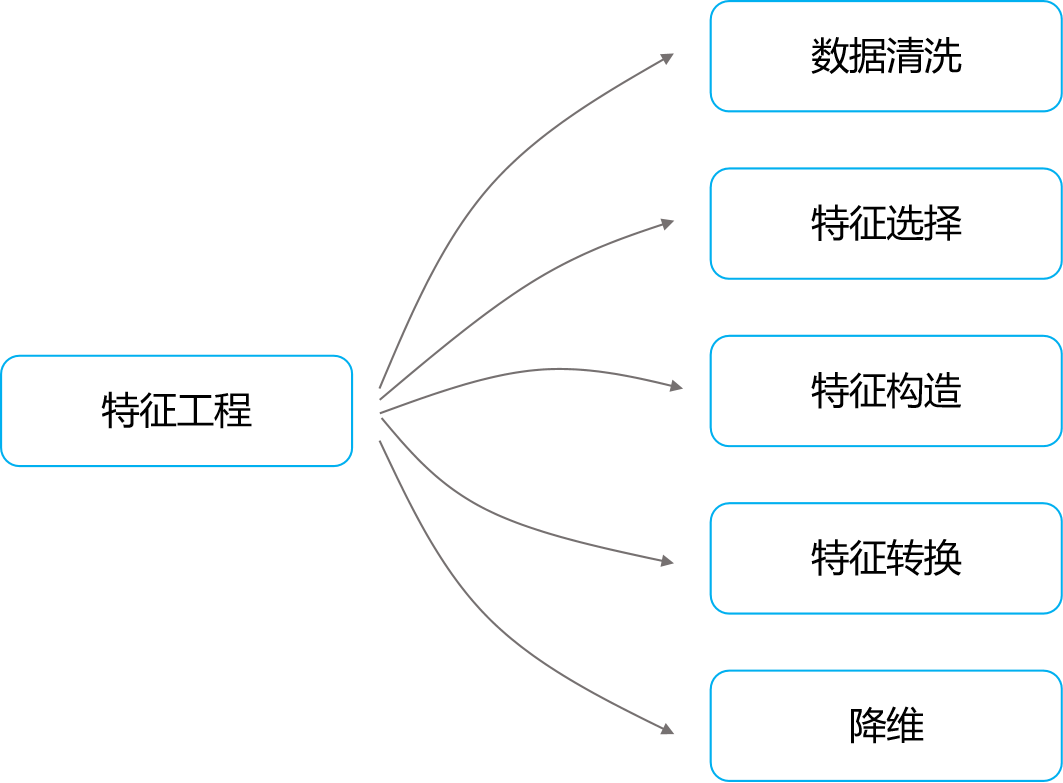
在实践中，收集到的数据往往是不完整、含有噪声和不一致的，这对模型的性能构成挑战，因为其很大程度上依赖于输入数据的质量，因此，特征工程应运而生。特征工程是数据预处理和机器学习的重要环节，包括从原始数据中选择、创建和转换特征。

主要内容

1.数据清洗

对原始数据进行缺失值处理、异常值处理和去除重复项等操作，为后续分析奠定基础。

1.1 缺失值处理

缺失值是数据集中常见的问题，处理缺失值的方法主要有以下几种：

删除：直接删除含有缺失值的行或列。这种方法简单直接，但当缺失数据较多时，可能会导致大量信息的丢失。

填充：使用某种策略填充缺失值，包括：

①使用平均数、中位数或众数等统计量填充缺失值；

②使用更复杂的方法，如基于模型的预测（如K最近邻、回归模型）来估计缺失值；

③使用向前或向后填充，如时间序列数据。

1.2 异常值处理

异常值（Outliers）是指在数据集中明显偏离其他观测值的数值。它们可能由于测量错误、数据录入错误和变异等原因产生。

识别异常值：

①标准差法：当数据服从正态分布，通常将超过平均值±2或3个标准差的数据点视为异常值；

②四分位数（IQR）法：IQR = Q3 - Q1。通常将 [Q1 - 1.5IQR，Q3 + 1.5IQR] 以外的数据点视为异常值；

③箱式图法：绘制 box 显示数据分布情况，基于上、下四分位数直观地识别异常值；

④Z-score法：将数据点换算成 Z-score：Z-score = (数据点 - 均值) / 标准差。把 |Z-score| > 2 or 3的数据点视为异常值。

处理异常值：

①删除；

②修正：包括使用平均值、中位数替换，分箱处理，模型预测值替代；

③保留：在某些情况下，异常值可能代表了重要的信息，需要保留。

1.3 去除重复项

数据集中可能存在重复的记录，这些重复项可能会导致模型训练时的偏差。常用 Python中的Pandas库检测和删除重复项。

1.4 数据一致性和格式规范化

保证数据的一致性和标准化，主要涉及：

格式：确保所有数据遵循相同的格式，如日期和时间格式统一，文本的大小写统一等。

数据类型：确保每列数据的类型正确，如将数字类型的数据从字符串转换为整数或浮点数。

2.特征选择

从原始数据中选择最有用的特征，以减少模型的复杂性和提高模型的性能。特征选择可以提高模型的训练效率，并减少模型过拟合的风险。主要方法有：

2.1 过滤法（Filter Methods）

在模型训练前，根据统计性质选择特征，与最终学习器的性能无关。该方法通过分析每个特征与目标变量之间的相关性，选择与目标变量最相关的特征。包括：

相关系数：使用皮尔逊相关系数、斯皮尔曼等级相关系数等方法来衡量连续特征与目标变量的相关性。

卡方检验：用于分类问题，检验类别变量与目标变量的独立性。

互信息和最大信息系数：评估变量之间的相互依赖性，不仅限于线性关系。

2.2 包裹法（Wrapper Methods）

在模型训练后，直接以最终学习器的性能作为特征的评价标准。该方法通过选择不同的特征子集，训练模型，并评估模型性能，以此决定哪些特征被选中。有：

序列特征选择算法：有向前选择、向后消除和双向搜索算法。每次操作都选择使模型性能最优化的特征。

2.3 嵌入法（Embedded Methods）

在模型训练中，通过学习算法自身的运行步骤选择特征，即算法自身包含特征选择步。包括：

基于惩罚项的特征选择方法：如L1正则化（Lasso）和L2正则化（Ridge）等。L1正则化能够将不重要的特征的系数压缩为0，从而实现特征的选择。

决策树：如随机森林、梯度提升树（Gradient Boosting Machines, GBM）等，它们在构建树的过程中评估特征的重要性。

3.特征构造

从现有数据中创造新特征，需结合专业知识与数据特征。特征构造可以揭示数据中隐藏的信息。常见方法有：

3.1 组合现有特征

对现有特征进行数学转换（如加减乘除、取对数等）来创造新特征。例如：在流行病学研究中，发病密度（Incidence Density）用于衡量在特定时间段内新发病例发生速率的方法，新特征——发病密度就可以通过新发病例数和总观察人时间计算。

$发病密度 = \frac{新发病例数}{总观察人时间}$

3.2 应用专业知识

应用专业知识创造出有意义的特征。例如：在医学领域，收集到一组人群的核酸检测结果，其中 CT值（阈值循环数，表示检测到病毒RNA所需的PCR循环次数）是一项计量特征，研究人员根据专业知识，把 CT值转换为二分类特征（核酸检测阳性、阴性）。

3.3 交互特征

将两个或多个特征组合在一起，应用于特征间存在复杂关系的情形。例如：在线性模型中，如果怀疑两个特征A和B之间存在交互作用，可以通过添加一个新特征 A*B 让模型学习这种关系。

3.4 多项式特征

通过将特征提升到更高的次方或创建特征的多项式组合来增加模型的复杂度和灵活性。适用于捕捉特征之间的非线性关系。

3.5 时间序列数据的特征构造

从时间维度提取信息，这些信息可以帮助模型理解数据随时间的变化趋势、周期性、季节性等特征。常用的时间序列特征构造方法有：

滞后特征（Lag Features）：引入过去的观测值作为新特征。例如：使用前一天（或多天）的数据作为今天的预测输入。适用于捕捉时间序列的自相关性。

滑动窗口统计（Rolling Window Statistics）：计算过去一段时间内的统计量（如均值、中位数、最大值、最小值、标准差等）作为特征。帮助模型捕捉到时间序列的短期趋势和波动。

时间分解特征：将时间戳分解为多个独立的组件（如年、月、日、周几、是否为节假日等）。有助于模型理解并利用时间序列的季节性和周期性。

傅里叶变换特征：通过傅里叶变换提取时间序列的频域特征，捕捉周期性变化。特别适用于处理具有明显周期性的时间序列。

4.特征转换

通过各种数学变换，处理偏斜数据、规范数据范围、转换非线性关系等。常见方法有：

4.1 标准化（Standardization）

使特征的均值为0，标准差为1。适用于大多数机器学习算法，尤其是基于梯度下降的算法（如线性回归、逻辑回归、神经网络）和包含距离计算的算法（如K-近邻、支持向量机）。

4.2 归一化（Normalization）

将特征的数值范围缩放到一个指定的范围，通常是0到1之间，或者是-1到1之间。通过将特征值减去最小值然后除以最大值与最小值的差来实现。应用场景：当数据包含多个特征且特征的尺度差异较大时。

4.3 对数转换（Log Transformation）

处理右偏（正偏）分布的数据，将其转换为接近正态分布。适用于处理具有长尾或极端值的特征，可以减少偏斜程度，使模型更稳定。

4.4 幂变换（Power Transformation）

减少数据的偏斜程度，改善特征与目标变量的线性关系。包括：平方、立方、平方根、立方根等。适用于当对数转换无法有效减少数据偏斜或当数据中包含零和负值时使用。

4.5 分箱（Binning）

将连续变量转换为分类变量，或者将多个类别合并成更少的类别。有助于减少噪声、处理异常值、简化模型和提高模型的泛化能力，在决策树中应用广泛。

4.6 布尔转换

选择一个阈值，特征值大于阈值的映射为1，否则为0。

4.7 编码

将类别特征转换为数值，常见方法有：独热编码（One-Hot Encoding）和标签编码（Label Encoding）

5.降维

通过减少数据集中的特征数量来简化模型，旨在减轻维度灾难、提高算法效率，同时尽可能保留原始数据的重要信息。常见方法有：

5.1 主成分分析（PCA）

原理：通过线性变换将原始数据变换为一组各维度线性无关的表示，称为主成分，主成分按照方差递减的顺序排列。

应用：用于连续数据的降维，常见于图像处理、数据可视化等领域。

优点：能够去除数据中的噪声，简化数据结构。

缺点：线性PCA可能不适用于解决非线性数据问题。

5.2 线性判别分析（LDA）

原理：旨在将数据投影到较低维度空间，同时保持不同类别数据的可分性最大化。

应用：常用于有监督的降维任务，如模式与信号分类。

优点：可以用于特征抽取，同时保留类别间最大的判别性。

缺点：需要预先知道标签信息，适用于分类问题而不是回归问题。