祝大家新年快乐!
今天这一次有点简单。
单调队列有两个要点,一个是单调,另一个就是我们的队列。
听到队列,我相信大家一定会想到它的好朋友BFS吧。但是……今天……可……没……那么……简单哦。
西佳佳偶像天团1
题目描述
西佳佳偶像天团共k人,最近n年每年有一位歌手加入。当人数超过k人时老团员自动退团。第i人的颜值为x[i],团内颜值最高者成为团长,求k人成团后每年的团长颜值是多少。
先试试样例八

输出样例:5 6 4 3 4 5 4 3 4 5 5 6
感觉有点难懂是吧,来来来,我们把他“具体化”一点。
固定长度滑动窗口最大值
单调队列主要解决的是这类问题↓

为了诠释这整个过程,我特意画了一张图
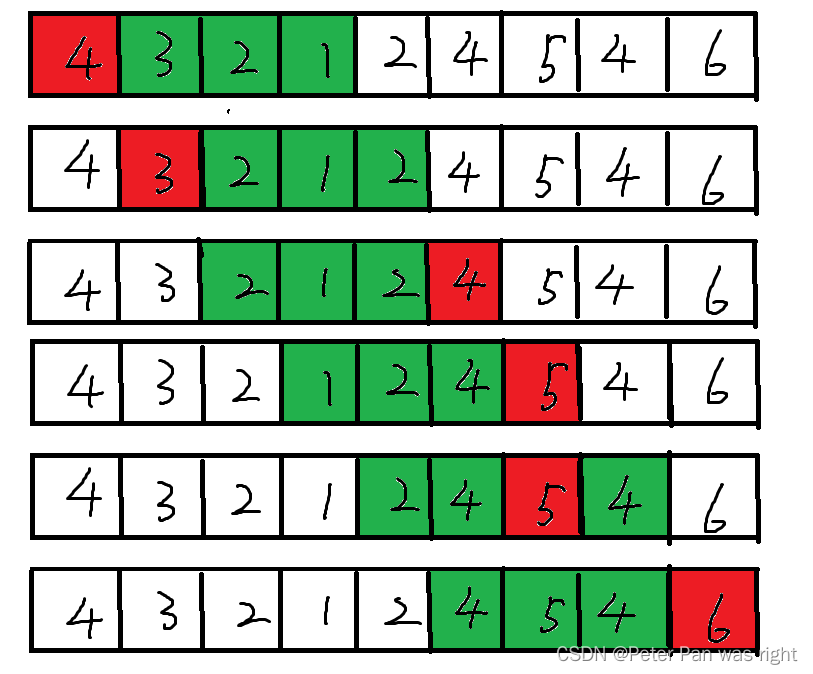
创作不易。
那么解决这类问题,我们有两种做法:1.平衡二叉查找树 2.单调队列。平衡二叉树我们用multiset实现;单调队列我们用数组模拟来实现,时间复杂度一样。
平衡二叉树
平衡二叉树分为红黑树、Splay树,Treap树。那么,我们用multiset实现,会比较简单
额……只不过把数组换成multiset而已
代码:
int n,k,x[N],ans[N];
cin>>n>>k;
for(int i=0;i<n;i++) cin>>x[i];
multiset<int> s;
for(int i=0;i<n;i++){s.insert(x[i]);if(i>=k) s.erase(s.find(x[i-k]));ans[i]=*s.rbegin();
}
for(int i=k-1;i<n;i++) cout<<ans[i]<<" ";单调队列
单调队列主要如下图
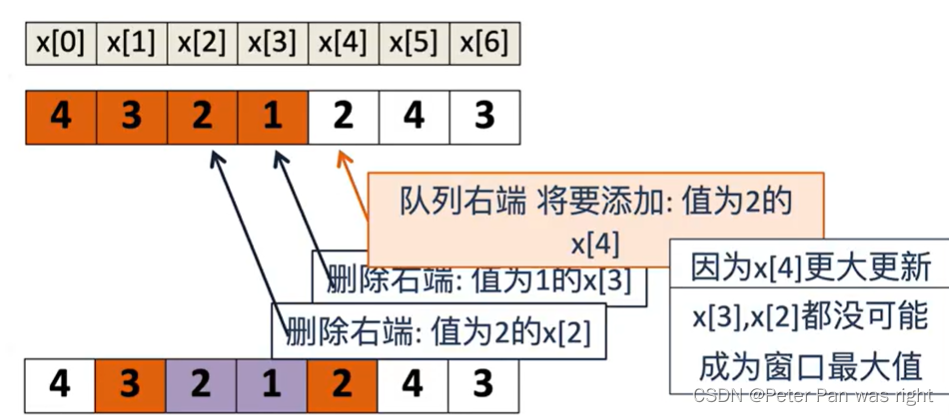
所以,这就是一个删除、的过程。没有用的就删除,有用的保留。简单的来说:每一次要加入新元素时,将新元素的值与队尾的值比较,若新元素的值大,则删除队尾,若队尾的值大,则将新元素直接插入队列。新一轮的滑动之后,从队首来看,如果它不在滑动窗口内,那么就删除它。大家用这个方法,再来试试前面的样例。注意:队列里存的是编号,不是值。大家想想时间复杂度为什么时O(n)呢?因为每个元素最多进队1次,出队1次,最坏时间复杂度为O(2n)≈O(n)。大家试试写写代码把。
//单调队列
cin>>n>>k;
fir(int i=0;i<n;i++) cin>>x[i];
int l=0,r=0;
for(int i=0;i<n;i++){while(l<r&&i-q[l]>=k) l++;while(l<r&&x[i]>x[q[r-1]]) r--;q[r++]=i;ans[i]=x[q[l]];
}
for(int i=k-1;i<n;i++) cout<<ans[i]<<" ";那么,总图我也给大家整理了,生怕你们看不懂
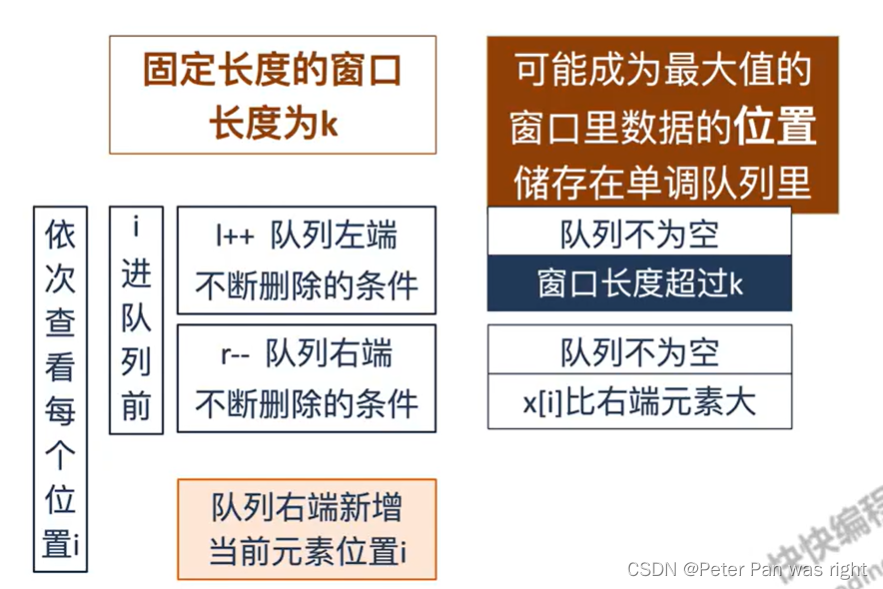
给大家看一个giao笑的代码

希望这些对大家有用,三连必回。最近两个月没有经常看CSDN,可能……会晚一点。