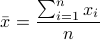1. 事务管理
1.1 事务回顾
在数据库阶段我们已学习过事务了,我们讲到:
事务是一组操作的集合,它是一个不可分割的工作单位。事务会把所有的操作作为一个整体,一起向数据库提交或者是撤销操作请求。所以这组操作要么同时成功,要么同时失败。
怎么样来控制这组操作,让这组操作同时成功或同时失败呢?此时就要涉及到事务的具体操作了。
事务的操作主要有三步:
-
开启事务(一组操作开始前,开启事务):start transaction / begin ;
-
提交事务(这组操作全部成功后,提交事务):commit ;
-
回滚事务(中间任何一个操作出现异常,回滚事务):rollback ;
1.2 Spring事务管理
1.2.1 案例
简单的回顾了事务的概念以及事务的基本操作之后,接下来我们看一个事务管理案例:解散部门 (解散部门就是删除部门)
需求:当部门解散了不仅需要把部门信息删除了,还需要把该部门下的员工数据也删除了。
步骤:
-
根据ID删除部门数据
-
根据部门ID删除该部门下的员工
代码实现:
-
DeptServiceImpl
@Slf4j
@Service
public class DeptServiceImpl implements DeptService {@Autowiredprivate DeptMapper deptMapper;
@Autowiredprivate EmpMapper empMapper;
//根据部门id,删除部门信息及部门下的所有员工@Overridepublic void delete(Integer id){//根据部门id删除部门信息deptMapper.deleteById(id);
//删除部门下的所有员工信息empMapper.deleteByDeptId(id); }
}-
DeptMapper
@Mapper
public interface DeptMapper {/*** 根据id删除部门信息* @param id 部门id*/@Delete("delete from dept where id = #{id}")void deleteById(Integer id);
}-
EmpMapper
@Mapper
public interface EmpMapper {
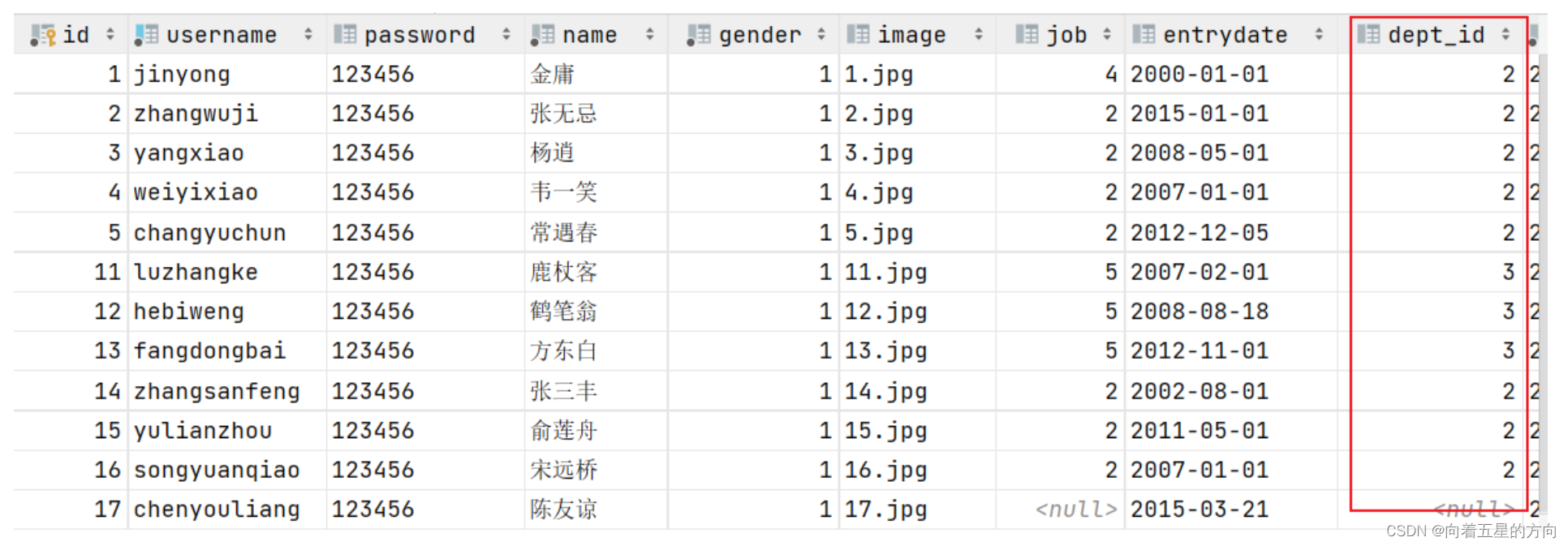
//根据部门id删除部门下所有员工@Delete("delete from emp where dept_id=#{deptId}")public int deleteByDeptId(Integer deptId);}重启SpringBoot服务,使用postman测试部门删除:
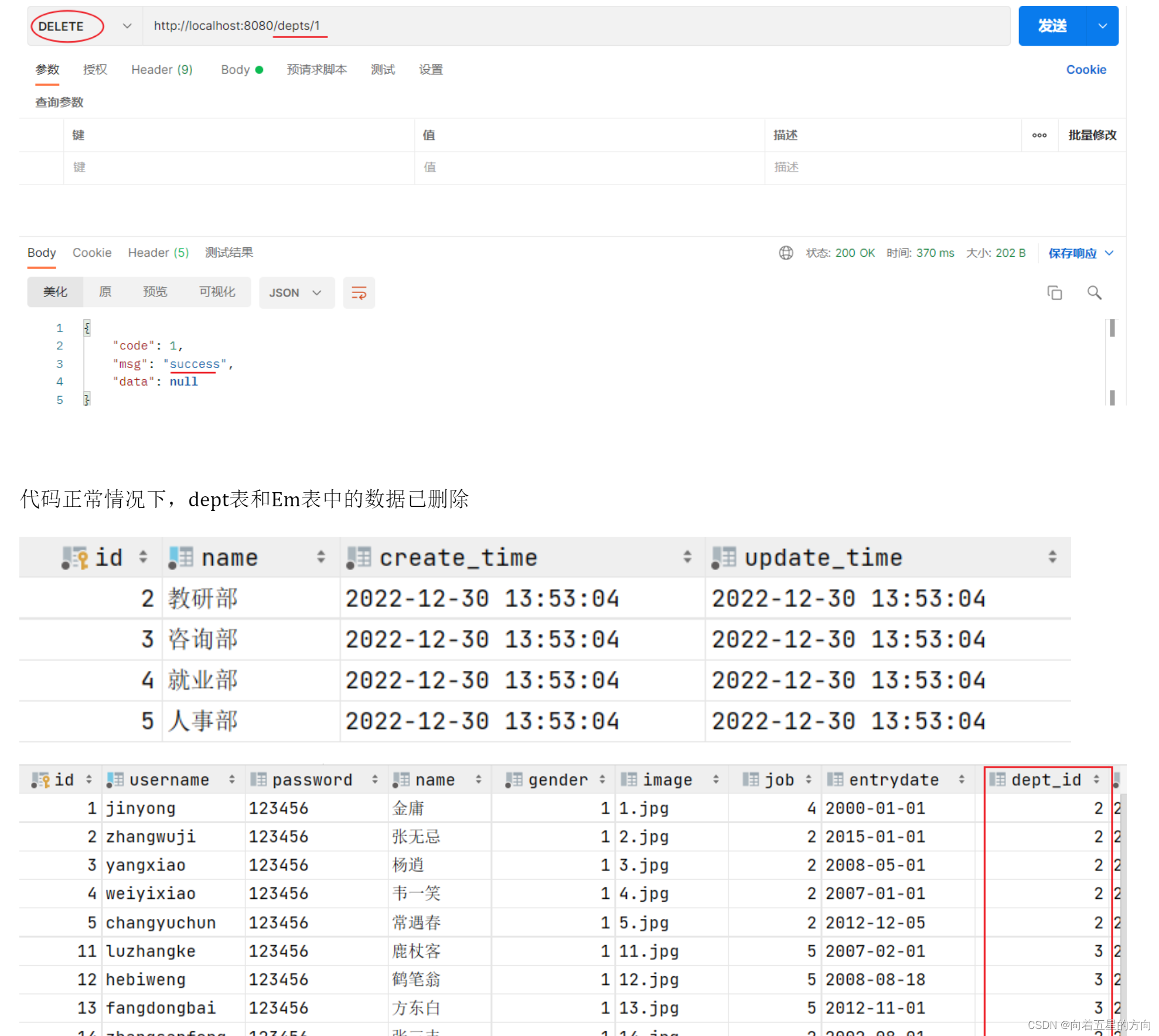
代码正常情况下,dept表和Em表中的数据已删除
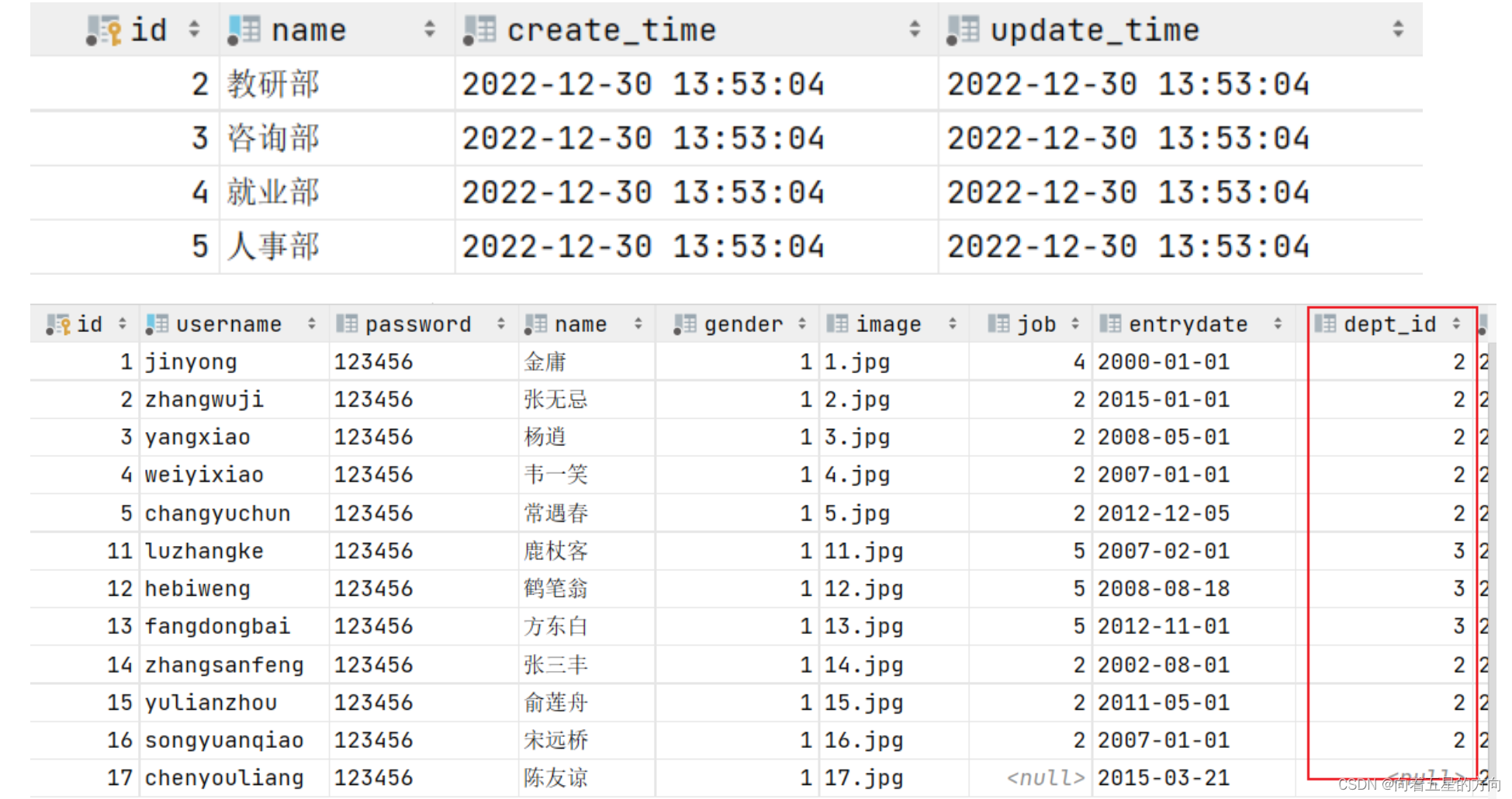
修改DeptServiceImpl类中代码,添加可能出现异常的代码:
@Slf4j
@Service
public class DeptServiceImpl implements DeptService {@Autowiredprivate DeptMapper deptMapper;
@Autowiredprivate EmpMapper empMapper;
//根据部门id,删除部门信息及部门下的所有员工@Overridepublic void delete(Integer id){//根据部门id删除部门信息deptMapper.deleteById(id);//模拟:异常发生int i = 1/0;
//删除部门下的所有员工信息empMapper.deleteByDeptId(id); }
}重启SpringBoot服务,使用postman测试部门删除:
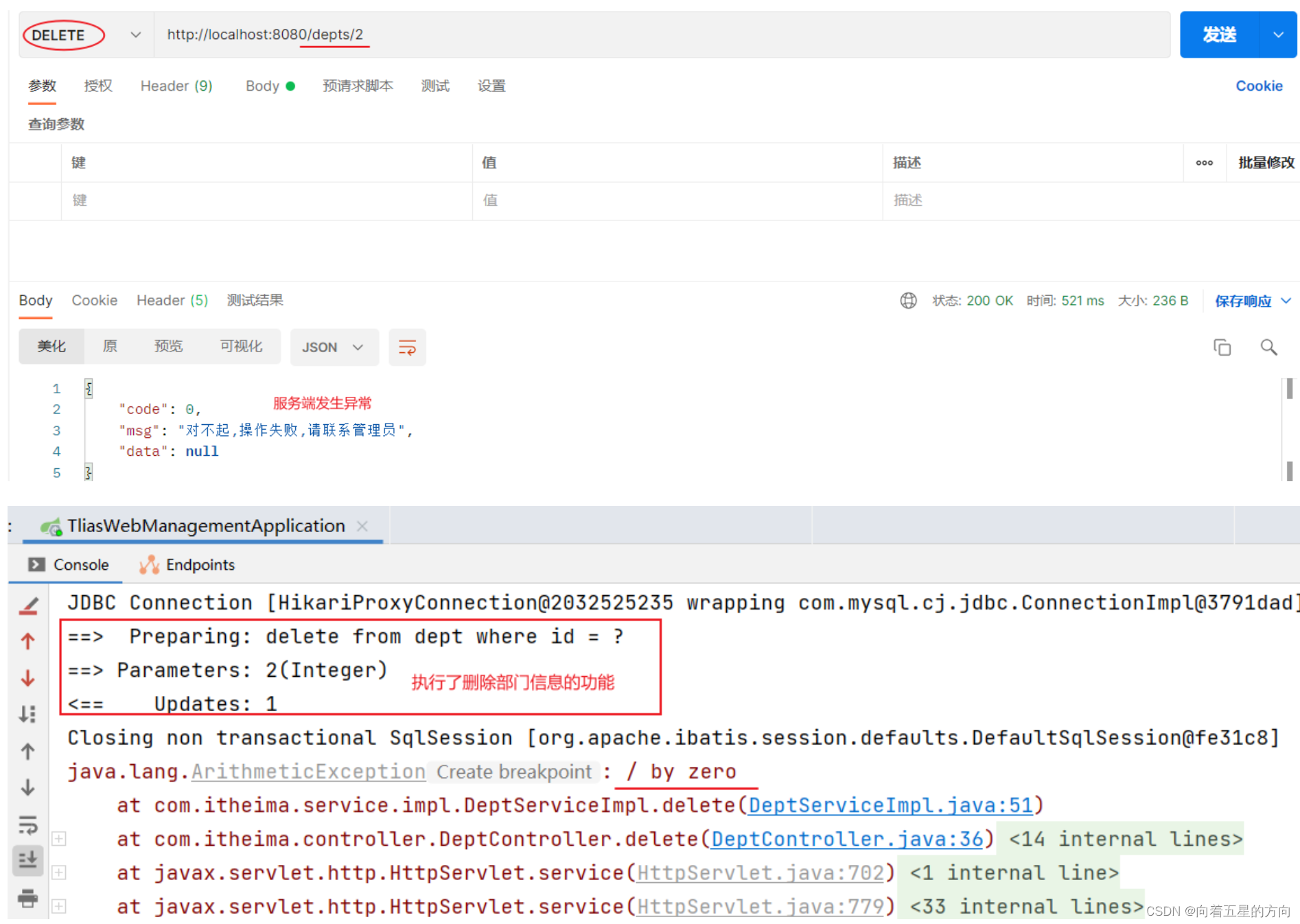
查看数据库表:
-
删除了2号部门
-

-
2号部门下的员工数据没有删除
-
以上程序出现的问题:即使程序运行抛出了异常,部门依然删除了,但是部门下的员工却没有删除,造成了数据的不一致。
1.2.2 原因分析
原因:
-
先执行根据id删除部门的操作,这步执行完毕,数据库表 dept 中的数据就已经删除了。
-
执行 1/0 操作,抛出异常
-
抛出异常之前,下面所有的代码都不会执行了,根据部门ID删除该部门下的员工,这个操作也不会执行 。
此时就出现问题了,部门删除了,部门下的员工还在,业务操作前后数据不一致。
而要想保证操作前后,数据的一致性,就需要让解散部门中涉及到的两个业务操作,要么全部成功,要么全部失败 。 那我们如何,让这两个操作要么全部成功,要么全部失败呢 ?
那就可以通过事务来实现,因为一个事务中的多个业务操作,要么全部成功,要么全部失败。
此时,我们就需要在delete删除业务功能中添加事务。
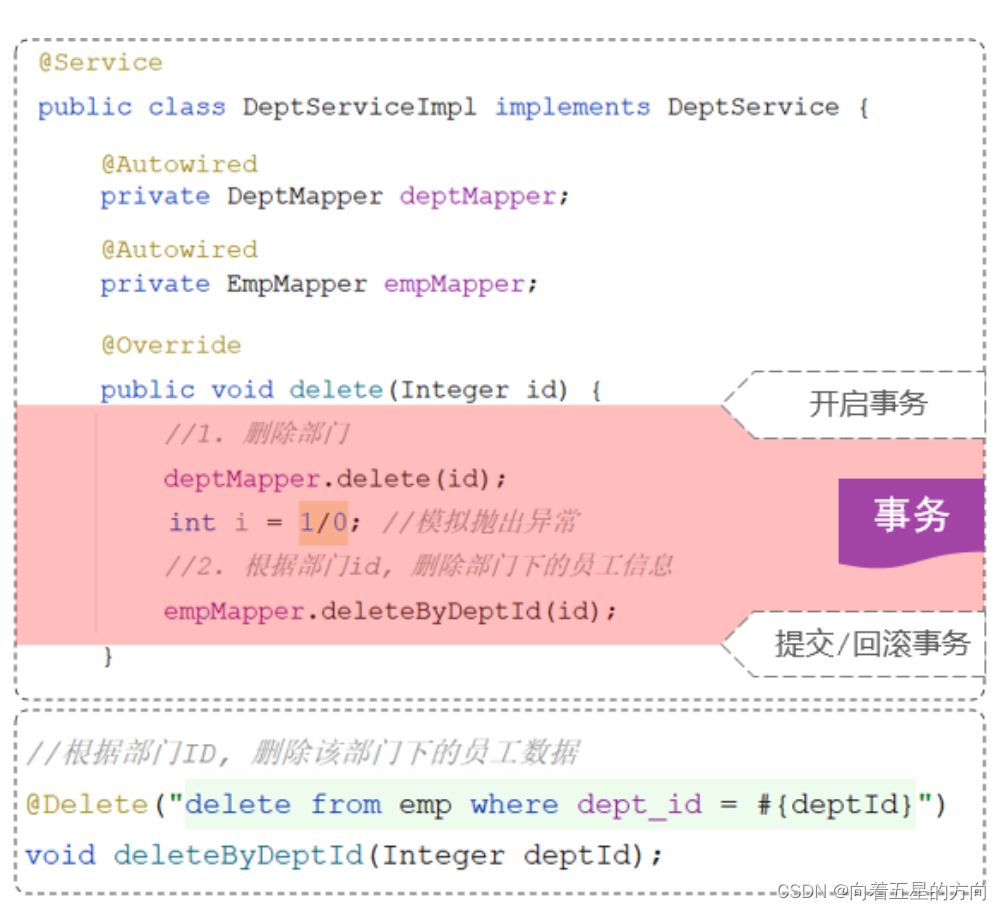
在方法运行之前,开启事务,如果方法成功执行,就提交事务,如果方法执行的过程当中出现异常了,就回滚事务。
思考:开发中所有的业务操作,一旦我们要进行控制事务,是不是都是这样的套路?
答案:是的。
所以在spring框架当中就已经把事务控制的代码都已经封装好了,并不需要我们手动实现。我们使用了spring框架,我们只需要通过一个简单的注解@Transactional就搞定了。
1.2.3 Transactional注解
@Transactional作用:就是在当前这个方法执行开始之前来开启事务,方法执行完毕之后提交事务。如果在这个方法执行的过程当中出现了异常,就会进行事务的回滚操作。
@Transactional注解:我们一般会在业务层当中来控制事务,因为在业务层当中,一个业务功能可能会包含多个数据访问的操作。在业务层来控制事务,我们就可以将多个数据访问操作控制在一个事务范围内。
@Transactional注解书写位置:
-
方法
-
当前方法交给spring进行事务管理
-
-
类
-
当前类中所有的方法都交由spring进行事务管理
-
-
接口
-
接口下所有的实现类当中所有的方法都交给spring 进行事务管理
-
接下来,我们就可以在业务方法delete上加上 @Transactional 来控制事务 。
@Slf4j
@Service
public class DeptServiceImpl implements DeptService {@Autowiredprivate DeptMapper deptMapper;
@Autowiredprivate EmpMapper empMapper;
@Override@Transactional //当前方法添加了事务管理public void delete(Integer id){//根据部门id删除部门信息deptMapper.deleteById(id);//模拟:异常发生int i = 1/0;
//删除部门下的所有员工信息empMapper.deleteByDeptId(id); }
}在业务功能上添加@Transactional注解进行事务管理后,我们重启SpringBoot服务,使用postman测试:
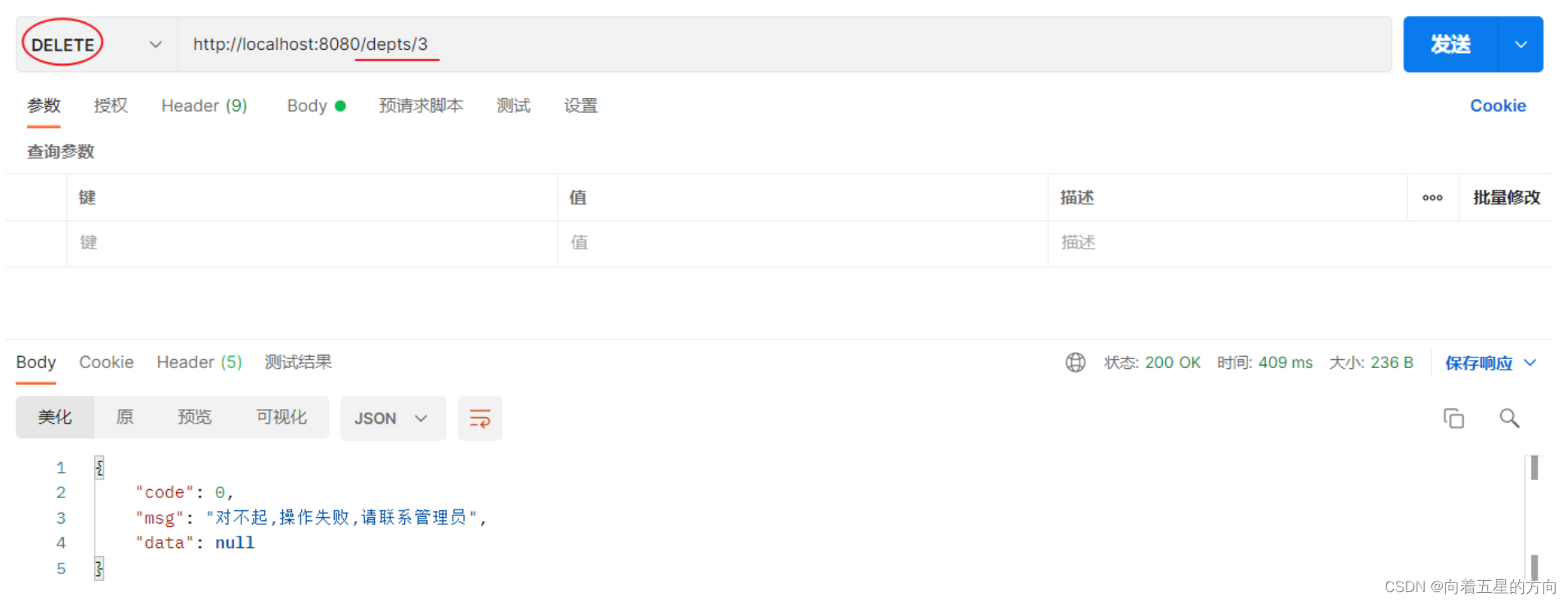
添加Spring事务管理后,由于服务端程序引发了异常,所以事务进行回滚。
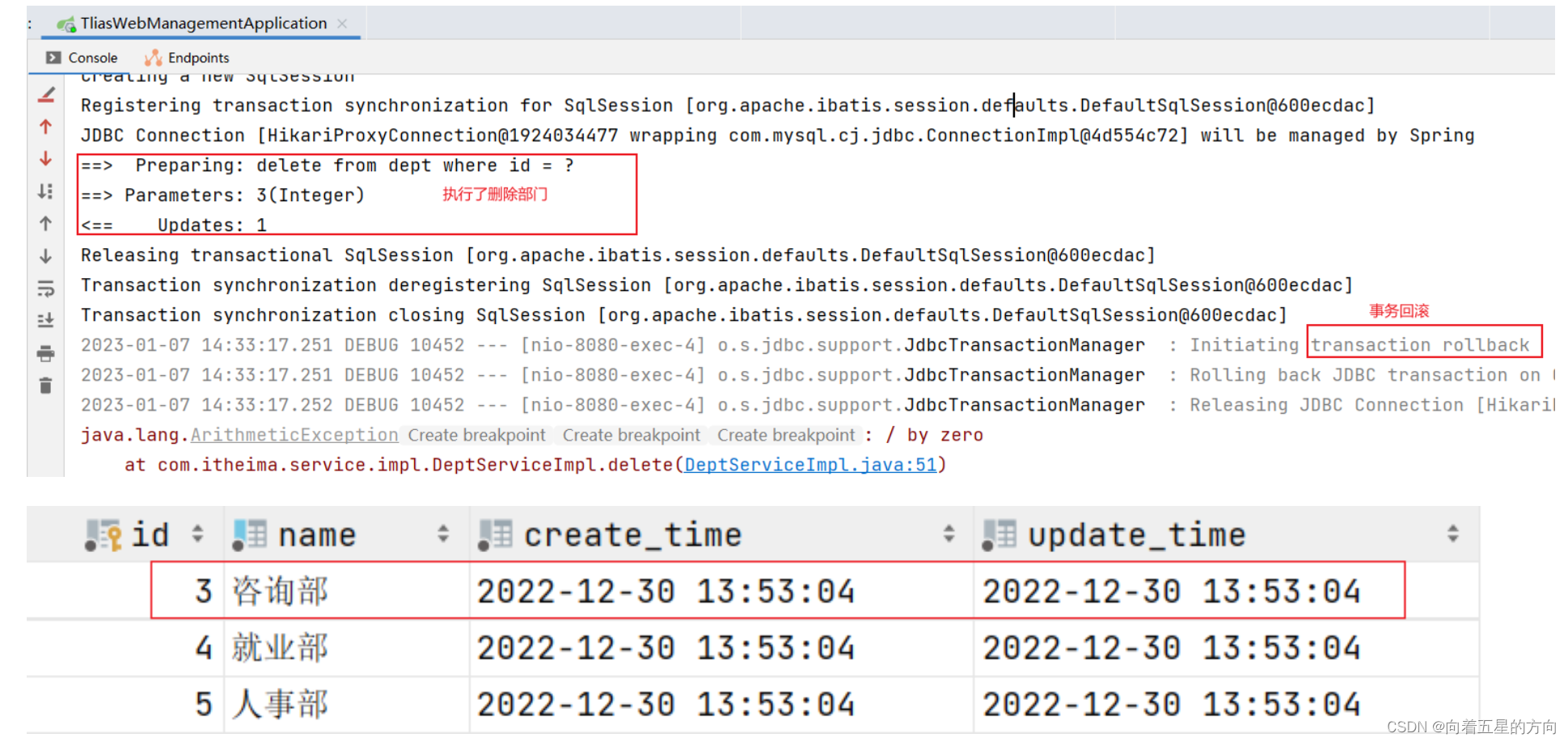
说明:可以在application.yml配置文件中开启事务管理日志,这样就可以在控制看到和事务相关的日志信息了
#spring事务管理日志
logging:level:org.springframework.jdbc.support.JdbcTransactionManager: debug