区间dp一般是先枚举区间长度,再枚举左端点,再枚举分界点,时间复杂度为
环形石子合并
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n−11 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54考了把环拆成链,把两个数组拼在一起可以达成 类环 的效果
比如 1 2 3 4 1 2 3 4
环可以是[1 2 3 4] [2 3 4 1] [3 4 1 2] [4 1 2 3]
这样就可以在石子合并的基础上增加微量时间复杂度的情况下做这道题了
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 410;int n;
int w[N], s[N];
int f[N][N], g[N][N];int main()
{IOScin >> n;for(int i = 1; i <= n; i ++){cin >> w[i];w[i + n] = w[i];}for(int i = 1; i <= n + n; i ++){s[i] = s[i - 1] + w[i];}memset(f, 0x3f, sizeof f);memset(g, -0x3f, sizeof g);for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n + n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = g[l][r] = 0;continue;}for(int k = l; k < r; k ++){f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);}}}int maxn = -2e9, minx = 2e9;for(int i = 1; i <= n; i ++){maxn = max(maxn, g[i][i + n - 1]);minx = min(minx, f[i][i + n - 1]);}cout << minx << endl;cout << maxn;return 0;
} 能量项链
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m×r×n(Mars 单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕⊕ 表示两颗珠子的聚合操作,(j⊕k) 表示第 j,k 两颗珠子聚合后所释放的能量。则
第 4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000,第 i 个数为第 i 颗珠子的头标记,当 i<N 时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
4≤N≤100,
1≤E≤2.1×1e9
输入样例:
4
2 3 5 10
输出样例:
710和上一题几乎一模一样
可以先枚举长度,再枚举首位端点,再枚举连接点
我写的代码不太一样,但结果都是一样的
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 210;int n;
int w[N];
ll f[N][N];int main()
{IOScin >> n;for(int i = 1; i <= n; i ++){cin >> w[i];w[i + n] = w[i];}memset(f, -0x3f, sizeof f);for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n + n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = 0;continue;}for(int k = l; k < r; k ++){f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + w[l] * w[k + 1] * w[r + 1]);}}}ll ans = -2e18;for(int i = 1; i <= n; i ++){ans = max(ans, f[i][i + n - 1]);}cout << ans;return 0;
} 加分二叉树
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。
每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第 1 行:一个整数 n,为节点个数。
第 2 行:n 个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第 1 行:一个整数,为最高加分(结果不会超过int范围)。
第 2 行:n 个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
n<30
输入样例:
5
5 7 1 2 10
输出样例:
145
3 1 2 4 5中序遍历一个数左边都是左子树的部分,一个数右边都是右子树的部分
所以可以用f[l, r]表示[l, r]区间内所有子树的最大值,去枚举每个点当根节点
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 40;int n;
int w[N];
int f[N][N], g[N][N];void dfs(int l, int r)
{if(l > r)return;int t = g[l][r];cout << t << ' ';dfs(l, t - 1);dfs(t + 1, r);
}int main()
{IOScin >> n;for(int i = 1; i <= n; i ++)cin >> w[i];for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = w[l];g[l][r] = l;continue;}for(int k = l; k <= r; k ++){int left = k == l ? 1 : f[l][k - 1];int right = k == r ? 1 : f[k + 1][r];int score = left * right + w[k];if(f[l][r] < score){f[l][r] = score;g[l][r] = k;}}}}cout << f[1][n] << endl;dfs(1, n);return 0;
}凸多边形的划分
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N,表示顶点数量。
第二行包含 N个整数,依次为顶点 1 至顶点 N 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50,
数据保证所有顶点的权值都小于1e9
输入样例:
5
121 122 123 245 231
输出样例:
12214884可以发现每条边只会参与一个三角形的构成
以1-n这条边为底,共有n-2种选法,设选了k这个点为顶点,那左边1~k和右面k~n两个区域明显是相互独立的,这就构成了区间dp的基础
枚举选顶点是哪个即可
这题虽然也是环但不需要拼起来,因为每个边只参与一次,选1 - n还是选2 - n+1都是一样的
另外需要用到高精度,可以先当成不需要高精度的写出来,再改成高精度,这样轻松一点
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 55, M = 35, INF = 2e9;int n;
int w[N];
ll f[N][N][M];//f[l,r]表示以l、r两点为边,以中间的一个顶点作为分界线 void add(ll a[], ll b[])
{ll tmp[M] = {0};ll t = 0;for(int i = 0; i < M; i ++){t += a[i] + b[i];tmp[i] = t % 10;t /= 10;}memcpy(a, tmp, sizeof tmp);
}void mul(ll a[], ll b)
{ll tmp[M] = {0};ll t = 0;for(int i = 0; i < M; i ++){t += a[i] * b;tmp[i] = t % 10;t /= 10;}memcpy(a, tmp, sizeof tmp);
}int cmp(ll a[], ll b[])
{for(int i = M - 1; i >= 0; i --){if(a[i] > b[i])return 1;if(a[i] < b[i])return -1;}return 0;
}void print(ll a[])
{ll t = M - 1;while(t && !a[t])t --;for(int i = t; i >= 0; i --)cout << a[i];cout << endl;
}int main()
{IOScin >> n;for(int i = 1; i <= n; i ++)cin >> w[i];ll tmp[M];for(int len = 3; len <= n; len ++){for(int l = 1; l + len - 1 <= n; l ++){int r = l + len - 1;//f[l][r] = INF;f[l][r][M - 1] = 1;for(int k = l + 1; k < r; k ++){memset(tmp, 0, sizeof tmp);tmp[0] = w[l];mul(tmp, w[r]);mul(tmp, w[k]);add(tmp, f[l][k]);add(tmp, f[k][r]);if(cmp(tmp, f[l][r]) < 0){memcpy(f[l][r], tmp, sizeof tmp);}//f[l][r] = min(f[l][r], f[l][k] + f[k][r] + w[l] * w[r] * w[k]);}}}//cout << f[1][n];print(f[1][n]);return 0;
}棋盘分割
将一个 8×8 的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了 (n−1)次后,连同最后剩下的矩形棋盘共有 n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
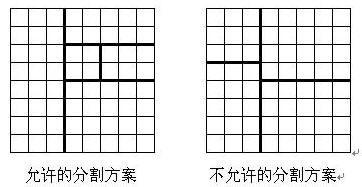
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n 块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
![]()
,其中平均值
![]()
,xi 为第 i 块矩形棋盘的总分。
请编程对给出的棋盘及 n,求出均方差的最小值。
输入格式
第 1 行为一个整数 n。
第 2 行至第 9 行每行为 8 个小于 100 的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1<n<15
输入样例:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
输出样例:
1.633f[x1][y1][x2][y1][k]表示左上角的点为(x1,y1),右下角的点为(x2,y2),这块区域要被分位k个点,表示均方差平方的最小值
由题可得n确定后平均值X也能确定
枚举时考虑横着切还是竖着切,切的时候考虑是留上边还是下边、左边还是右边
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 9, M = 15, INF = 2e9;int n, m = 8;
int s[N][N];
double f[N][N][N][N][M];
double X;double get(int x1, int y1, int x2, int y2)
{double res = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] - X;return res * res / n;
}double dp(int x1, int y1, int x2, int y2, int k)
{double &v = f[x1][y1][x2][y2][k];if(v >= 0)return v;if(k == 1)return get(x1, y1, x2, y2);v = INF;for(int i = x1; i < x2; i ++){v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));v = min(v, get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));}for(int j = y1; j < y2; j ++){v = min(v, dp(x1, y1, x2, j, k - 1) + get(x1, j + 1, x2, y2));v = min(v, get(x1, y1, x2, y2) + dp(x1, j + 1, x2, y2, k - 1)); }return v;
}int main()
{//IOScin >> n;for(int i = 1; i <= m; i ++){for(int j = 1; j <= m; j ++){cin >> s[i][j];s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];}}X = (double)s[m][m] / n;memset(f, -1, sizeof f);double t = dp(1, 1, m, m, n);printf("%.3lf", sqrt(t));return 0;
}