纯粹容器 - 洛谷

首先先看几个通用的知识点：

1.费马小定理+快速幂求逆元（求倒数）

当mod为质数的时候可以使用费马小定理

ll ksm(int x, int y) {if (x == 1) return 1;ll res = 1, base = x;while (y) {if (y & 1) res = (res * base) % mod;base = (base * base) % mod;y >>= 1;}return res;
}
int inv(int aim)//inverse element{return ksm(aim, mod - 2);
}

2.动态规划预处理组合数

i个里面选j个

公式：C[i][j] = C[i-1][j] +C[i-1][j-1] 。

组合公式理解, 从 i 里选 j 个的方案数由两部分，设k是 i 中某一个, 则选取 k 和不选取 k ：C[i-1][j] + C[i-1][j-1]

（第i个选或不选）

初始化 C[ i ][ 0 ] = 1; （起源都算一种）

int C[105][105] = { 0 };
C[0][0] = 1;for (int i = 1; i <= n; i++){C[i][0] = 1;for (int j = 1; j <= i; j++){C[i][j] = (C[i - 1][j] + C[i-1][j - 1]) % mod;}}

3.单调栈本题做法

每个数（的下标）都入栈，当栈顶数小于当前数的时候，为栈顶数记录同时pop

期望的定义：

（大学概率论有）

将期望转化成概率求和的原理涉及到概率论中的期望值的定义。期望值是随机变量的加权平均值，而这个加权是根据每个可能结果发生的概率来进行的。

具体来说，对于一个离散型随机变量X，其期望值E(X)可以表示为：

E(X) = Σ x * P(X=x)

其中，x表示随机变量X可能取到的值，P(X=x)表示X取到值x的概率。

对于一个连续型随机变量X，其期望值E(X)可以表示为：

E(X) = ∫ x * f(x) dx

其中，f(x)表示X的概率密度函数。

因此，将期望转化成概率求和的原理就是根据每个可能结果发生的概率，将每个结果乘以对应的概率，然后将所有结果的加权平均值作为期望值。

本题期望：

“请你对每个容器求出它存活轮数的期望”

E = 求和 ：存活i轮*存活i轮的概率

然而许多题解给出了这样的式子，

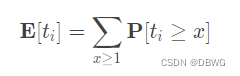
其实就是上式的转化

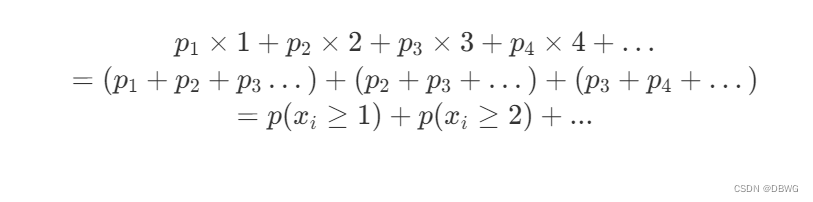
（我在此忏悔，这个式子不是我推的，我来第一步都没有列，脑子硬想，，）

样例解释：

对于输入#1有两种情况:

先碰3 1，然后碰2

或者先碰1 2，然后碰3

每种情况，3都能活2回合，2都能活1回合，1都是第一次就碎掉。

对于输入#2也是两种：

先碰12再碰3                        1活0,2活1,3活2

或者先碰23再碰1                1活1,2活0,3活2

按定义的期望计算：

1： 活一次 1/2

2：活一次1/2

求逆元即使输出：

代码：

int C[105][105] = { 0 };
ll ksm(int x, int y) {if (x == 1) return 1;ll res = 1, base = x;while (y) {if (y & 1) res = (res * base) % mod;base = (base * base) % mod;y >>= 1;}return res;
}
int inv(int aim)//inverse element{return ksm(aim, mod - 2);
}
void solve(int c)
{int n;cin >> n;vector<int>arr(n + 2);vector<int>left(n + 2);vector<int>right(n + 2);stack<int>st1,st2;for (int i = 1; i <= n; i++){cin >> arr[i];}//“单调栈，为栈内右边最近的大的，所以现存栈内都是逆序小的，遇到大的挨着出栈for (int i = 1; i <= n; i++){while (st1.size() && arr[i] > arr[st1.top()]){right[st1.top()] = i-st1.top();st1.pop();}st1.push(i);}for (int i = n; i >= 1; i--){while (st2.size() && arr[i] > arr[st2.top()]){left[st2.top()] = st2.top()-i;st2.pop();}st2.push(i);}//组合数处理：C[0][0] = 1;for (int i = 1; i <= n; i++){C[i][0] = 1;for (int j = 1; j <= i; j++){C[i][j] = (C[i - 1][j] + C[i-1][j - 1]) % mod;}}for (int i = 1; i <= n; i++){int ans = 0;for (int j = 1; j < n; j++)//轮数{int la = 0, lb = 0, lab = 0;if (left[i] && j >= left[i]){//la = C[n-1-left[i]][j-left[i]] / C[n-1][j];la = C[n-1-left[i]][j-left[i]] * inv( C[n-1][j])%mod;}if (right[i] && j >= right[i]){lb = C[n - 1 - right[i]][j - right[i]] * inv(C[n - 1][j]) % mod;}if (left[i] && right[i] && j >= left[i] + right[i]){lab = C[n-1-left[i]-right[i]][j-left[i]-right[i]] *inv( C[n - 1][j])%mod;}ans = (ans + 1 + mod - la + mod - lb + lab) % mod;}cout << ans << " ";}}signed main()
{//ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;//cin >> t;for (int i = 1; i <= t; i++){solve(i);}return 0;
}