一、最小生成树算法

稠密图使用prim算法，稀疏图使用kruskal算法

 

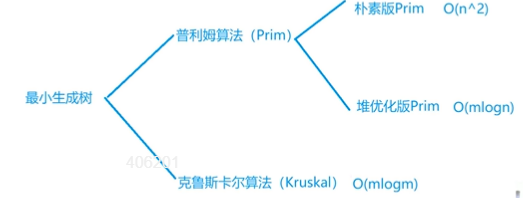
   二、prim算法求最小生成树

prim和dijkstra算法类似，都是找到符合某种条件的点，然后更新。prim使用到已经构成的部分最小树所有结点中最小的距离。dijkstra算法是使用到起点最小的距离。

#include<bits/stdc++.h>
//858 prim最小生成树 （稠密图做法）
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int prim()
{int res=0;for(int i=0;i<n;i++){//找最短的边int t=-1;for(int j=1;j<=n;j++){//只要这个点没有进入集合，或者还没初始化//没有进入集合而且边权较少if(!st[j]&&(t==-1||dist[t]>dist[j]))t=j;}//如果经过一个循环之后t找到的最短边仍然是INF，但是在第一次的时候所有的都是INFif(i&&dist[t]==INF)return INF;st[t]=true;//由于存在负权自环所以在更新与点相连的所有边之前就保存边if(i) res+=dist[t];//展示了与dijkstra算法的不同之处，dist保存的是边，而不是某种路for(int j=1;j<=n;j++)dist[j]=min(dist[j],g[t][j]);}return res;
}int main()
{cin>>n>>m;memset(g,0x3f,sizeof g);memset(dist,0x3f, sizeof dist);for(int i=0;i<m;i++){int a,b,c;cin>>a>>b>>c;g[a][b]=min(g[a][b],c);}int ans=prim();if(ans==INF)puts("impossible");else cout<<ans<<endl;
}

三、kruskal算法

思路简单：

#include<bits/stdc++.h>
//858 prim最小生成树 （稠密图做法）
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int p[N];
struct Edge
{int a,b,w;bool operator <(const Edge &W)const{return w<W.w;}
}edges[N];int find(int a)
{if(p[a]==a)return a;else  p[a]=find(p[a]); return p[a];
}
int main()
{cin>>n>>m;for(int i=0;i<m;i++){int a,b,c;cin>>a>>b>>c;edges[i]={a,b,c};}sort(edges,edges+m);for(int i=0;i<=n;i++)p[i]=i;int res=0,cnt=0;//遍历所有边for(int i=0;i<m;i++){//访问的顺序是有序的，只要连接的两个点没有在一个连通块里面int a=edges[i].a,b=edges[i].b,c=edges[i].w;a=find(a),b==find(b);if(a!=b){p[a]=b;//将其连接res+=c;cnt++;}}if(cnt!=n-1)puts("impossible");else cout<<res<<endl;
}

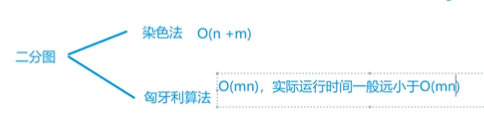
 四、二分图（染色法判断是否有奇数环）

一个图是二分图当且仅当图中不含有奇数环（环中边的数量是奇数）

如果图当中不含有奇数环染色过程中没有矛盾。

思路：因为有多个连通块，而每次dfs就把连通块里面的所有的点全部遍历了，然后找其他连通块里面的点。

染色法dfs判断奇数环：对于当前点连接的所有边，判断这个点是否已经被染色，没有被染色继续染色，染色了，如果和相连的点的颜色相同，说明有奇数环。

#include<bits/stdc++.h>
//858 prim最小生成树 （稠密图做法）
using namespace std;
const int N=100010,M=200010;
int m,n;
int color[N];//染色情况
int e[N],ne[N],h[N],idx;
void add(int a,int b)
{//e保存边idx的终点是什么//ne保存idx这条边连接的下一条边//更新h的值e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
//对一个连通块进行深度优先遍历
bool dfs(int u,int c)
{color[u]=c;for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];if(!color[j]){//只要有一个不通就返回falseif(!dfs(j,3-c))return false;}else if(color[j]==c)return false;}return true;}
int main()
{//cmemset(color,0,sizeof color);memset(h,-1,sizeof h);cin>>n>>m;for(int i=0;i<m;i++){int a,b,c;cin>>a>>b;add(a,b),add(b,a);}int flag=0;//遍历所有还没有遍历到的连通块，for(int i=1;i<=n;i++){if(!color[i]){if(!dfs(i,1))//随便取一个颜色，因为相邻两次循环就{flag=1;break;}}}if(flag) puts("No");else puts("Yes");}

五、匈牙利算法（两组结点最多的匹配）

首先按照第一选择进行匹配，后面匹配冲突的时候，去看先匹配的那个可不可以调整。

使用bool数组st保证回去调整的时候不会选到同一个点，也就是一个点不会被同一个点匹配到两次。

#include<bits/stdc++.h>
//861二分图的最大匹配(匈牙利算法)
using namespace std;
const int N=500,M=100010;
int e[N],ne[M],h[N],idx;
int st[N];
int match[N],n1,n2,m;
void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}int find(int u)
{for(int i=h[u];i!=-1;i=ne[i])//与u相连的所有点{int j=e[i];//因为可能在调整的过程中重复调用find函数，此时st[j]已经为true//不会再选这个点了if(!st[j])//之前有没有被考虑过{st[j]=true;//如果与其相连的点没有匹配//或者匹配了但是可以更换if(match[j]==0||find(match[j])){//匹配上一个点match[j]=u;return true;}}}//尝试了所有的出边所连的点都不行的时候return false;
}
int main()
{cin>>n1>>n2>>m;while(m--){int a,b;cin>>a>>b;add(a,b);}int res=0;for(int i=1;i<=n1;i++){if(find(1))res++;}cout<<res<<endl;
}