题目描述

数独是一种填数字游戏，英文名叫 Sudoku，起源于瑞士，上世纪 70 年代由美国一家数学逻辑游戏杂志首先发表，名为 Number Place，后在日本流行，1984 年将 Sudoku 命名为数独，即 “独立的数字” 的缩写，意思是 “在每一格只有一个数字”。

2004 年，曾任中国香港高等法院法官的高乐德 (Wayne Gould) 把这款游戏带到英国，成为英国流行的数学智力拼图游戏。

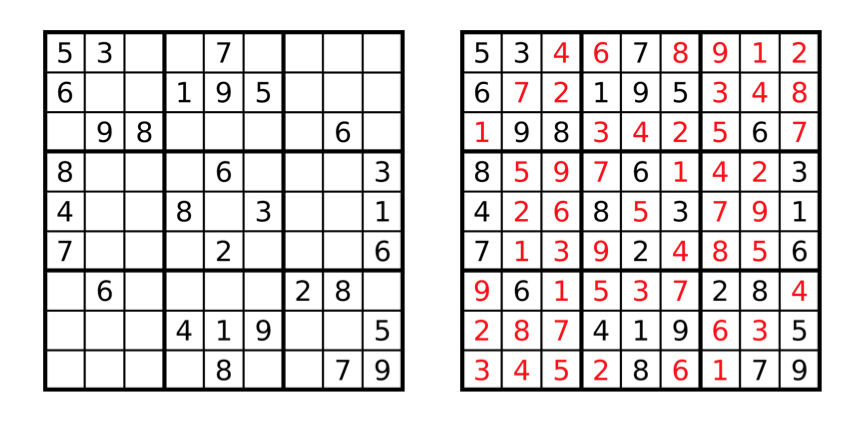
玩家需要根据 9×99 \times 99×9 盘面上的已知数字，推理出所有剩余位置的数字，并满足每一行、每一列、每一个粗线九宫格内的数字包含有 1-9 的数字，且不重复。

现在给你一个数独，请你解答出来。每个数独保证有且只有一个解。

输入描述:

输入仅一组数据，共 9 行 9 列，表示初始数独（其中 0 表示数独中的空位）。

输出描述:

输出共 9 行 9 列，表示数独的解。注意⾏末没有空格。

示例1

输入

5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9

输出

5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9

想法：

本来我以为只要处理了行冲突和列冲突，九宫格冲突就自然而然可以消除了，其实是不行的，有点想当然了，又没去验证，直接这么写了。还有就是之前的写法中递归dfs函数那里，感觉写错了。我想写的是找出数独中没填的然后去填，但是这种写法遇到已经填了的格子的话就会直接结束，而不会再去找没填的空格，根本无法遍历整个数独。代码如下。

void dfs(int x,int y){
    if(x>9) {
        for(int i=1;i<=9;i++){
            for(int j=1;j<=9;j++){
                cout<<sd[i][j];
                if(j!=9) cout<<' ';
                else cout<<endl;
            }
        }
        return ;
    }
    int xx=x,yy=y;
    if(y<9) yy+=1;
    else { xx+=1,yy=1;}
    if(sd[xx][yy]==0){
        for(int i=1;i<=9;i++){
            if(r[xx][i]==0&&c[yy][i]==0){
                sd[xx][yy]=i;//填数字
                dfs(xx,yy);
                sd[xx][yy]=0;
            } 
        }
    }
}

然后我就修改了，可是吧，还是不行，没有输出。感觉改了还是错了，首先对于整个数组我全都标记了行冲突，列冲突，没分类。其次呢，我dfs递归的终止条件好像没用。最后，我在填数字时又没有标记行冲突，列冲突。反正很多问题吧。

代码：

#include<bits/stdc++.h>
using namespace std;
int sd[15][15];
int r[15][15];
int c[15][15];
void dfs(int x,int y){
    if(x>9) {
        for(int i=1;i<=9;i++){
            for(int j=1;j<=9;j++){
                cout<<sd[i][j];
                if(j!=9) cout<<' ';
                else cout<<endl;
            }
        }
        return ;
    }
    for(int i=x;;i++){
        for(int j=y+1;j<=9;j++){
            if(sd[i][j]==0){
                for(int k=1;k<=9;k++){
                    if(r[i][k]==0&&c[j][k]==0){
                        sd[i][j]=k;//填数字
                        dfs(i,j);
                        sd[i][j]=0;
                        break;//
                    } 
                }
            }
        }
    }
}
int main(){
    for(int i=1;i<=9;i++){
        for(int j=1;j<=9;j++){
            cin>>sd[i][j];
            r[i][sd[i][j]]=1;
            c[j][sd[i][j]]=1;
        }
    }
            dfs(1,1);
}

网课：

我的想法和她的想法就是搜的复杂度不同，我是一格一格搜，她是只搜没填的空格。用了个结构体数组来记录没填的格子数量和下标。九宫格冲突图也处理得很巧妙，标记好各个九宫格的序号，然后处理。

代码：

#include<bits/stdc++.h>
using namespace std;
int r[15][15],c[15][15],jgg[15][15];
int sd[15][15];
struct Mt{
    int x,y;
} mt[100];
int cnt=0;
int xh[15][15]={{0,0,0,0,0,0,0,0,0,0},//序号
                {0,1,1,1,2,2,2,3,3,3},
                {0,1,1,1,2,2,2,3,3,3},
                {0,1,1,1,2,2,2,3,3,3},
                {0,4,4,4,5,5,5,6,6,6},
                {0,4,4,4,5,5,5,6,6,6},
                {0,4,4,4,5,5,5,6,6,6},
                {0,7,7,7,8,8,8,9,9,9},
                {0,7,7,7,8,8,8,9,9,9},
                {0,7,7,7,8,8,8,9,9,9}
               };
void dfs(int gs){
    if(gs>=cnt){
        for(int i=1;i<=9;i++){
            for(int j=1;j<=9;j++){
                cout<<sd[i][j];
                if(j!=9) cout<<' ';
                else cout<<endl;
            }
        }
        return ;
    }
    for(int i=1;i<=9;i++){
        if(r[mt[gs].x][i]) continue;
        if(c[mt[gs].y][i]) continue;
        if(jgg[xh[mt[gs].x][mt[gs].y]][i]) continue;
        jgg[xh[mt[gs].x][mt[gs].y]][i]=1,r[mt[gs].x][i]=1,c[mt[gs].y][i]=1;
        sd[mt[gs].x][mt[gs].y]=i;
        dfs(gs+1);
        jgg[xh[mt[gs].x][mt[gs].y]][i]=0,r[mt[gs].x][i]=0,c[mt[gs].y][i]=0;
    }
}
int main(){
    for(int i=1;i<=9;i++){
        for(int j=1;j<=9;j++){
            cin>>sd[i][j];
            if(sd[i][j]==0) { mt[cnt].x=i , mt[cnt].y=j; cnt++;}
            else {r[i][sd[i][j]]=1,c[j][sd[i][j]]=1,jgg[xh[i][j]][sd[i][j]]=1;}
        }
    }
    dfs(0);
}