黄金分割比的无理性
“黄金分割比的神奇之处:视觉化证明与数学的魅力”
人们在学习高等数学时,走到一个证明的结尾处,通常会经历这样的思考:“我理解每一行是怎样由前一行得到的,但是我却不明白为什么这个定理是正确的,人们是怎样想到这个论证的。”我们经常想从证明中得到更多的东西,而不仅仅是确信它的正确性。读过一个好的证明之后,我们会感到它对定理进行了一番阐明,使我们理解了之前所不理解的一些东西。
由于人类大脑有很大一部分是用于处理视觉数据的,我们也就不难理解有很多论证都用到了我们的视觉能力。为了说明这一点,我将给出另一个关于无理性的证明,这一回是所谓的黄金分割比。几百年来,这个数一直使非数学家为之着迷(数学家也着迷,只是程度较轻)。它是具有如下特征的矩形的长宽比:从矩形中切掉一个正方形,剩下一个小矩形,它旋转之后恰与原始矩形的形状完全一样。下图中的第二个矩形正是这种情况。
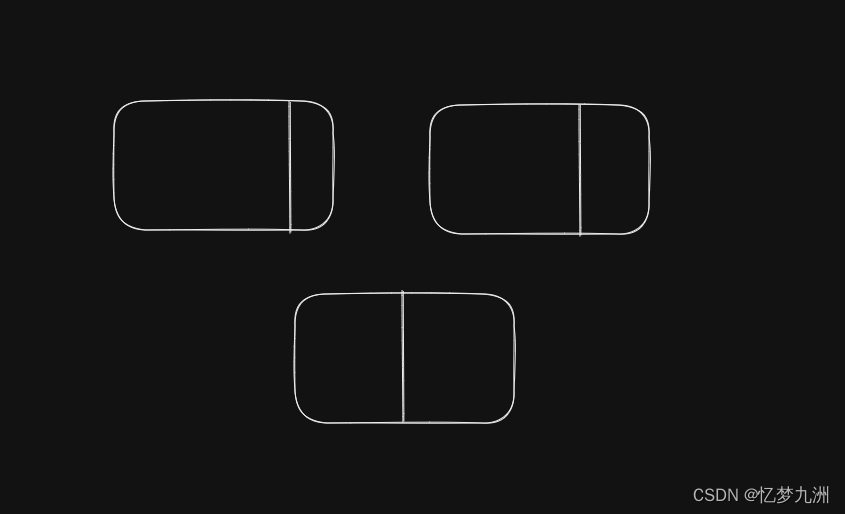
“黄金分割比的存在与几何操作的奇妙关联”
为什么这样的边长比是存在的?(数学家已经被训练得惯于提出这类问题。)要回答它可以换一个角度,想象一个小矩形从正方形的一侧生长出来,使整个图形变成一个大矩形。刚开始的时候,小矩形很长很瘦,而大矩形仍然差不多是个正方形。如果我们让小矩形继续生长,直到它自己变成一个正方形,那大短形的长就是宽的两倍。所以,小矩形最开始的时候比大矩形瘦得多,现在却比大矩形胖(相对于各自的尺寸来讲)。在这两者之间必存在一点,使得两个矩形形状相同。上图说明了这样的过程。
还可以用另一种方式来考虑黄金分割比的存在,那就是把它算出来。如果我们把它叫作x,并假设正方形的边长为1,那么大矩形的边长就是1和x,小矩形的边长是x-1和1。如果它们的形状相同,那么 x = x 1 = 1 x − 1 x=\frac{x}{1}=\frac{1}{x-1} x=1x=x−11。两端同时乘以x-1,我们就得到 x ( x − 1 ) = 1 x(x-1)=1 x(x−1)=1,所以 x 2 − x − 1 = 0 x^2-x-1=0 x2−x−1=0。求解这个二次方程,并且知道x不是负数,我们就得出 x = 1 + 5 2 x=\frac{1+\sqrt{5}}{2} x=21+5。(如果你在数学上很有造诣,或者深入理解了上一个系列,你可能会问为什么我如此确信, 5 \sqrt{5} 5存在。实际上,这第二种论证正是要把几何问题归结于一个等价的代数问题。)
得出了比例x存在之后,让我们来考虑对边长为x和1的矩形进行如下的操作。首先,从中切掉一个正方形,由黄金分割比的定义,剩下的小矩形与原来的矩形形状相同。然后再不断地重复这一基本操作,得到一系列越来越小的矩形,每一个的形状都与之前的形状相同,因而长宽比都是黄金分割比。很显然,这一过程永远不会终止。(参见下图的第一个矩形。)
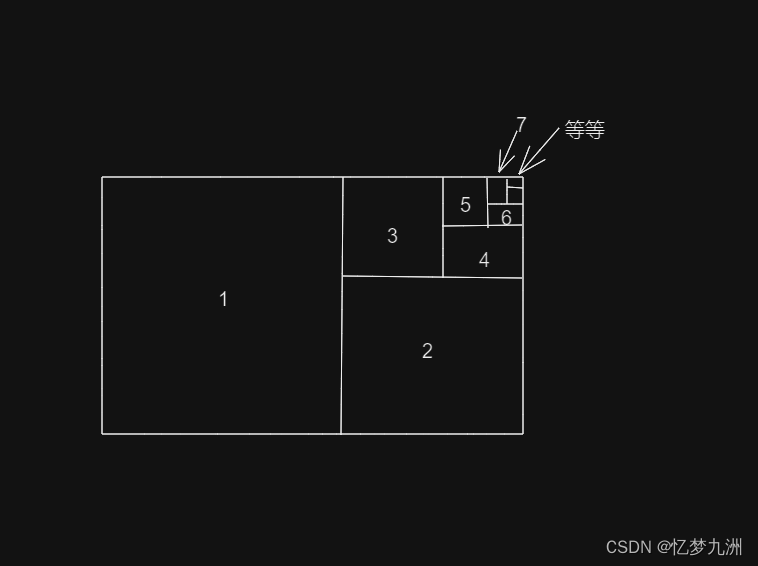

“黄金分割比的无理性:通过几何操作的比较证明”
现在让我们对长宽比为p/q的矩形施行同样的操作,其中p和q都是整数。也就是说,这个矩形与边长为p和q的矩形形状相同,因而可以被分成pq个小正方形,如上图中的第二个矩形所示。如果我们从这个矩形的一端切掉一些大正方形会怎么样呢?如果q小于p,那么我们切掉一个qq的正方形,得到一个q*(p-q)的矩形。我们可以继续切掉下一个正方形,依此类推。这个过程会永远持续下去吗?不会。每次切掉的正方形都是小方格的整数倍,我们不可能操作多于pq的次数——因为一开始就只有pq个小方格。
我们表明了如下两个事实。
- 如果矩形的边长比是黄金分割比,那么我们可以一直从中切掉正方形,没有尽头。
- 如果矩形的边长比是某对整数p和q的比值p/q,那么就不能永不停止地从中切掉正方形。
于是我们可以得到,比值p/q不是黄金分割比,无论p和q取什么值。换言之,黄金分割比是无理数。
仔细思考上面这个证明,你最终会发觉,虽然乍看它和之前对 2 \sqrt{2} 2是无理数的证明很不一样,但实际上也并无太大区别。不过,我们将它呈现出来的方式确实不同——而且对很多人来说,这种方式更有吸引力。
总结
黄金分割比是一种具有神奇性质的数值,它在几何形状和数学运算中展现了其存在与无理性。通过视觉化证明和几何操作的比较,我们可以理解黄金分割比的存在。从切割矩形的过程中,我们可以观察到黄金分割比的形成和不断重复,而对于其他边长比例,这个过程会终止。这些证明揭示了黄金分割比的特殊性质,并展示了数学的魅力和深奥之处。黄金分割比作为一种无理数,一直吸引着数学家和非数学家的兴趣,展现了数学中丰富的思维和推理过程。