DS：顺序栈的实现

                                                    创作不易，友友们给个三连吧！！

一、栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

二、顺序栈的实现

数组实现栈：

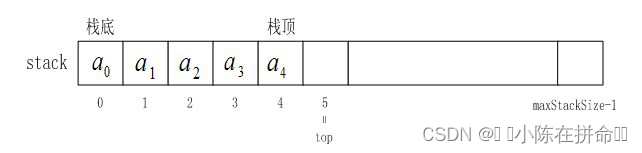
首元素当栈低，栈顶是数组的尾元素，压栈就是尾插，出栈就是尾删

链表实现栈：

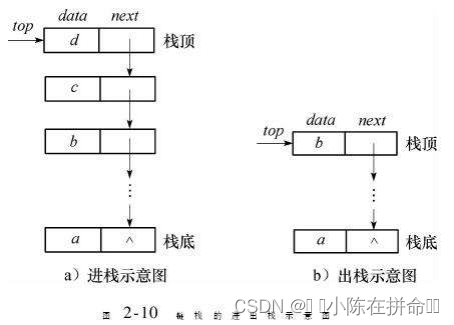
链表的最后一个结点当栈底，栈顶是链表的头结点，压栈就是头插，出栈就是头删

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

由于这些操作和顺序表的实现基本上是一样的，所以以下的介绍不做详细讲解。

建议大家看看博主关于顺序表的实现，再来看下面代码就易如反掌了！！

DS：顺序表的实现-CSDN博客

2.1 栈相关结构体

下面是定长的静态栈的结构，实际中一般不实用，因为设置得太小容易不够，设置得太大容易浪费

typedef int STDataType;
#define N 10
typedef struct Stack
{STDataType _a[N];int _top; // 栈顶
}Stack;

以我们主要实现下面的支持动态增长的栈

typedef int STDataType;
//支持动态增长的栈
typedef struct Stack
{STDataType* a;int top;//栈顶int capacity;//栈容量
}Stack;

2.2 初始化栈

void StackInit(Stack* ps)
{ps->a = NULL;ps->top = ps->capacity = 0;
}

     ps->top并不指向栈顶元素，而是指向栈顶元素的下一个位置，如果想要指向栈顶元素，则需要给top赋值-1.但是给top赋值0也有好处，就是top的值就相当于是顺序表中的size，即表示栈中的有效数据个数

2.3 压栈

void StackPush(Stack* ps, STDataType x)
{assert(ps);//判断是否需要扩容if (ps->top == ps->capacity){int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* temp = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);if (temp == NULL){perror("realloc fail");exit(1);}ps->a = temp;ps->capacity = newcapacity;}//压栈ps->a[ps->top++] = x;
}

2.4 出栈

void StackPop(Stack* ps)
{assert(ps);//如果栈为空，则没有删除的必要assert(!StackEmpty(ps));ps->top--;
}

2.5 获取栈顶元素

STDataType StackTop(Stack* ps)
{assert(ps);//如果栈为空，不可能有栈顶元素assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}

要注意:因为我们初始化的top是0，所以top指向的是栈顶元素的下一个位置！ 

2.6 获取栈中有效元素个数

int StackSize(Stack* ps)
{assert(ps);return ps->top;
}

因为top初始赋值为0， 所以top其实就相当于栈中的有效数据个数，专门封装一个函数只是想提高可读性！

2.7 检测栈是否为空

bool StackEmpty(Stack* ps)
{assert(ps);return ps->top == 0;
}

      在顺序表中，是否为空只需要看有效容量个数是不是0即可，但是在顺序栈中有效数据个数size被替换成了 top，虽然我们知道top和size的意思差不多，但是如果在代码里直接用的话可读性就没有size这么好，所以单独设置一个检测栈是否为空的函数。

2.8 销毁栈

void StackDestory(Stack* ps)
{free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}

2.9 打印栈 

     栈相比较于顺序表，并不具备随机访问的特点，因为栈是后进先出的，也就是说如果我们要遍历栈去访问栈中的每个元素，那么就需要一边获取栈顶元素一边出栈，这其实就会破坏原先栈的结构了，一般只能使用一次，不具备复用性，因此没必要单独封装一个函数。如果实在想打印栈，那么就在main函数中这样测试一下

#include"Stack.h"int main()
{Stack sk;StackInit(&sk);StackPush(&sk, 1);StackPush(&sk, 2);StackPush(&sk, 3);StackPush(&sk, 4);while (!StackEmpty(&sk)){printf("%d ", StackTop(&sk));//一边打印栈顶元素StackPop(&sk);//一边出栈}
}

三、顺序栈实现的所有代码 

3.1 Stack.h

#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>typedef int STDataType;
//支持动态增长的栈
typedef struct Stack
{STDataType* a;int top;//栈顶int capacity;//栈容量
}Stack;void StackInit(Stack* ps);//初始化栈
void StackPush(Stack* ps, STDataType x);//入栈
void StackPop(Stack* ps);//出栈
STDataType StackTop(Stack* ps);//获取栈顶元素
int StackSize(Stack* ps);//获取栈中有效元素个数
bool StackEmpty(Stack* ps);//检测栈是否为空，为空返回true
void StackDestory(Stack* ps);//销毁栈

3.2 Stack.c

#include"Stack.h"void StackInit(Stack* ps)
{ps->a = NULL;ps->top = ps->capacity = 0;
}void StackPush(Stack* ps, STDataType x)
{assert(ps);//判断是否需要扩容if (ps->top == ps->capacity){int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* temp = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);if (temp == NULL){perror("realloc fail");exit(1);}ps->a = temp;ps->capacity = newcapacity;}//压栈ps->a[ps->top++] = x;
}void StackPop(Stack* ps)
{assert(ps);//如果栈为空，则没有删除的必要assert(!StackEmpty(ps));ps->top--;
}STDataType StackTop(Stack* ps)
{assert(ps);//如果栈为空，不可能有栈顶元素assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}int StackSize(Stack* ps)
{assert(ps);return ps->top;
}bool StackEmpty(Stack* ps)
{assert(ps);return ps->top == 0;
}void StackDestory(Stack* ps)
{free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}

3.3 test.c(测试)

#include"Stack.h"int main()
{Stack sk;StackInit(&sk);StackPush(&sk, 1);StackPush(&sk, 2);StackPush(&sk, 3);StackPush(&sk, 4);while (!StackEmpty(&sk)){printf("%d ", StackTop(&sk));//一边打印栈顶元素StackPop(&sk);//一边出栈}
}

 四、栈的相关oj题

4.1 选择题

1、一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出
栈的顺序是（B）。
A  12345ABCDE
B  EDCBA54321
C  ABCDE12345
D  54321EDCBA
解析：后进先出的特点，进栈过程中如果没有出栈，入栈和出栈的顺序是相反的。

2.若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（C）
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1
解析：虽然是后进先出，但是入栈和出栈顺序相反是相对的，重点就是要判断进栈过程中是否有出栈，题目有明确提出这一点，所以这题最好同过画图去排除可能性，比如C，3出栈说明1和2都在栈内，下一个要出栈的话只能是2不能是1,1不可能在2的前面出栈。

4.2 有效的括号（OJ题） 

有效的括号（力扣）

条件的意思是：括号可以相互包含，放不能参差摆放

思路：利用栈结构后进先出的特点，让左括号入栈，右括号出栈匹配，当左右括号相等的前提下，如果最后栈为空，则符合题目要求，左括号大于右括号和右括号大于左括号要分开讨论。

typedef char STDataType;
//支持动态增长的栈
typedef struct Stack
{STDataType* a;int top;//栈顶int capacity;//栈容量
}Stack;
void StackInit(Stack* ps);//初始化栈
void StackPush(Stack* ps, STDataType x);//入栈
void StackPop(Stack* ps);//出栈
STDataType StackTop(Stack* ps);//获取栈顶元素
int StackSize(Stack* ps);//获取栈中有效元素个数
bool StackEmpty(Stack* ps);//检测栈是否为空，为空返回true
void StackDestory(Stack* ps);//销毁栈
void StackInit(Stack* ps)
{ps->a = NULL;ps->top = ps->capacity = 0;
}void StackPush(Stack* ps, STDataType x)
{assert(ps);//判断是否需要扩容if (ps->top == ps->capacity){int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* temp = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);if (temp == NULL){perror("realloc fail");exit(1);}ps->a = temp;ps->capacity = newcapacity;}//压栈ps->a[ps->top++] = x;
}void StackPop(Stack* ps)
{assert(ps);//如果栈为空，则没有删除的必要assert(!StackEmpty(ps));ps->top--;
}STDataType StackTop(Stack* ps)
{assert(ps);//如果栈为空，不可能有栈顶元素assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}int StackSize(Stack* ps)
{assert(ps);return ps->top;
}bool StackEmpty(Stack* ps)
{assert(ps);return ps->top == 0;
}void StackDestory(Stack* ps)
{free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}bool isValid(char* s) 
{Stack st;StackInit(&st);while(*s){if(*s=='('||*s=='{'||*s=='[')StackPush(&st,*s);else{//如果右比左多，栈为空if(StackEmpty(&st)){StackDestory(&st);return false;}char top=StackTop(&st);StackPop(&st);//不匹配if((*s==')'&&top!='(')||(*s=='}'&&top!='{')||(*s==']'&&top!='[')){StackDestory(&st);return false;}}++s;}//如果左括号比右括号多，栈也有元素bool ret=StackEmpty(&st);StackDestory(&st);return ret;
}

要注意中间的条件判断！！ 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/2777736.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！

相关文章

[神奇代码岛】皮肤功能使用

[神奇代码岛】皮肤功能使用

前言 最近有很多人在制作地图的时候&#xff0c;因该会用到皮肤的功能&#xff0c;但是皮肤操作只知道UI操作&#xff0c;但缺点是&#xff0c;只能设置地图默认皮肤&#xff0c;根本都做不到想要的什么皮肤购买功能&#xff0c;自主穿戴功能&#xff0c;而API官方又放在非常隐…
阅读更多...
python爬虫入门（一）

python爬虫入门（一）

使用requests 库获取网站html信息 import requests response requests.get("https://jingyan.baidu.com/article/17bd8e52c76b2bc5ab2bb8a2.html#:~:text1.%E6%89%93%E5%BC%80%E6%B5%8F%E8%A7%88%E5%99%A8F12%202.%E6%89%BE%E5%88%B0headers%E9%87%8C%E9%9D%A2%E7%9A%84…
阅读更多...
【C++】初识模板：函数模板和类模板

【C++】初识模板：函数模板和类模板

目录 一、模板函数 1、函数模板的概念 2、函数模板的格式 3、函数模板的原理 4、函数模板实例化 5、 模板参数的匹配原则 二、类模板 1 、类模板的定义格式 2 、类模板的实例化 3、模板类示例 一、模板函数 1、函数模板的概念 函数模板代表了一个函数家族&#xff0c…
阅读更多...
2024年安全员-B证证模拟考试题库及安全员-B证理论考试试题

2024年安全员-B证证模拟考试题库及安全员-B证理论考试试题

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 2024年安全员-B证证模拟考试题库及安全员-B证理论考试试题是由安全生产模拟考试一点通提供&#xff0c;安全员-B证证模拟考试题库是根据安全员-B证最新版教材&#xff0c;安全员-B证大纲整理而成&#xff08;含2024年…
阅读更多...
比较6*6范围内7个点182个结构的顺序

比较6*6范围内7个点182个结构的顺序

( A, B )---6*30*2---( 1, 0 )( 0, 1 ) 让网络的输入有6个节点&#xff0c;训练集AB各由6张二值化的图片组成&#xff0c;让A中有7个点&#xff0c;让B全是0&#xff0c;收敛误差7e-4&#xff0c;收敛199次&#xff0c;统计迭代次数平均值并排序。 得到顺序为 用6个点的结构标…
阅读更多...
【Godot4.2】图片处理函数库 - textureDB

【Godot4.2】图片处理函数库 - textureDB

概述 Godot中节点使用的图片是Texture2D或其子类型&#xff0c;而涉及图片处理&#xff0c;大多数功能在Image类型中&#xff0c;并且我们通常需要频繁的构造Image和ImageTexture类型。 为了封装构造Image和ImageTexture类型的代码&#xff0c;提供直接从文件到直接可以赋值给…
阅读更多...
python 基础知识点（蓝桥杯python科目个人复习计划36）

python 基础知识点（蓝桥杯python科目个人复习计划36）

今日复习计划&#xff1a;DFS搜索基础 1.简介 搜索方法&#xff1a;穷举问题解空间部分&#xff08;所有情况&#xff09;&#xff0c;从而求出问题的解。 深度优先搜索&#xff1a;本质上是暴力枚举 深度优先&#xff1a;尽可能一条路走到底&#xff0c;走不了再回退。 2…
阅读更多...
《零基础实践深度学习》波士顿房价预测任务 02

《零基础实践深度学习》波士顿房价预测任务 02

1.3 波士顿房价预测任务 上一节我们初步认识了神经网络的基本概念&#xff08;如神经元、多层连接、前向计算、计算图&#xff09;和模型结构三要素&#xff08;模型假设、评价函数和优化算法&#xff09;。本节将以“波士顿房价预测”任务为例&#xff0c;向读者介绍使用Pytho…
阅读更多...
C#在设备数据采集中的应用

C#在设备数据采集中的应用

设备数据采集在现代工业生产中扮演着至关重要的角色。随着工业互联网的发展&#xff0c;设备数据采集技术已经成为了智能制造的基础之一。在这篇文章中&#xff0c;我们将探讨C#语言在设备数据采集中的应用。 首先&#xff0c;让我们来了解一下设备数据采集的概念。设备数据采集…
阅读更多...
购物|电商购物小程序|基于微信小程序的购物系统设计与实现(源码+数据库+文档)

购物|电商购物小程序|基于微信小程序的购物系统设计与实现(源码+数据库+文档)

电商购物小程序目录 目录 基于微信小程序的购物系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户前台功能实现 2、管理员后台功能实现 四、数据库设计 1、实体ER图 2、具体的表设计如下所示&#xff1a; 五、核心代码 六、论文参考 七、最新计算机毕设…
阅读更多...
使用SpringMVC实现功能

使用SpringMVC实现功能

目录 一、计算器 1、前端页面 2、服务器处理请求 3、效果 二、用户登陆系统 1、前端页面 &#xff08;1&#xff09;登陆页面 &#xff08;2&#xff09;欢迎页面 2、前端页面发送请求--服务器处理请求 3、效果 三、留言板 1、前端页面 2、前端页面发送请求 &…
阅读更多...
day45_maven_tomcat

day45_maven_tomcat

今日内容 0 复习昨日 1 maven 2 tomcat 3 创建项目 0 复习昨日 1 单词写5遍 argument 参数 parameter 参数 access 访问 field 字段 invoke 调用 illegal 非法 invalid 无效 column 列 property 属性 DataSource 数据源 2 数据库连接池有啥好处 3 获得字节码文件的方式 Class.f…
阅读更多...
如何从 Windows 硬盘恢复丢失或删除的照片

如何从 Windows 硬盘恢复丢失或删除的照片

您是否曾经不小心删除了无法再恢复的重要照片&#xff1f;如果这是您的商务或家庭照片、婚礼或童年回忆或者亲人的照片怎么办&#xff1f; 根据我们的经验&#xff0c;用户在清理计算机以提高存储/速度时通常会遇到此类事故&#xff0c;并最终删除包含重要图片的文件夹&#x…
阅读更多...
VUE基础知识八 ElemrntUI使用

VUE基础知识八 ElemrntUI使用

使用VUE脚手架以及在项目里引入ElementUI&#xff0c;上一章节讲过了&#xff0c;本章节就不赘述了。 ElementUI官网 所有使用ElementUI的组件&#xff0c;在使用时&#xff0c;都是以el-组件名开头的 一 按钮组件 ElementUI里的组件都是类似的&#xff0c;这里以按钮组件来…
阅读更多...
AWD-Test2

AWD-Test2

1.已知账号密码&#xff0c;可SSH连接进行代码审计。2.登录可万能密码进入&#xff0c;也可注册后登录。3.修改url参数&#xff0c;发现报错。确定为Linux系统4.写入一句话&#xff0c;并提交。&#xff08;也可以文件上传&#xff0c;这里采用简洁的方法&#xff09; <?p…
阅读更多...
macbookair怎么清理内存 ？如何利用 CleanMyMac X 进行系统清理

macbookair怎么清理内存 ？如何利用 CleanMyMac X 进行系统清理

macbookair怎么清理内存 清理MacBook Air的内存可以通过以下几种方法&#xff1a; 优化储存空间。在MacBook Air上&#xff0c;可以通过“优化储存空间”来释放空间。这包括将文件储存在iCloud中&#xff0c;如桌面、文稿和iCloud信息&#xff0c;以及自动移除在iCloud中观看…
阅读更多...
〖大前端 - ES6篇②〗- let和const

〖大前端 - ES6篇②〗- let和const

说明&#xff1a;该文属于 大前端全栈架构白宝书专栏&#xff0c;目前阶段免费&#xff0c;如需要项目实战或者是体系化资源&#xff0c;文末名片加V&#xff01;作者&#xff1a;哈哥撩编程&#xff0c;十余年工作经验, 从事过全栈研发、产品经理等工作&#xff0c;目前在公司…
阅读更多...
一文讲透Python函数中的形式参数和实际参数

一文讲透Python函数中的形式参数和实际参数

函数参数包括形式参数和实际参数&#xff0c;简称形参和实参。其中形式参数即是在定义函数时函数后面括号中的参数列表&#xff08;parameterlist&#xff09;&#xff0c;比如上一个帖子的示例中的width, length&#xff1b;实际参数则是调用函数时函数后面括号中的参数值&…
阅读更多...
Qt PCL学习（三）：点云滤波

Qt PCL学习（三）：点云滤波

注意事项 版本一览&#xff1a;Qt 5.15.2 PCL 1.12.1 VTK 9.1.0前置内容&#xff1a;Qt PCL学习&#xff08;一&#xff09;&#xff1a;环境搭建、Qt PCL学习&#xff08;二&#xff09;&#xff1a;点云读取与保存 0. 效果演示 1. pcl_open_save.pro QT core guigr…
阅读更多...
Linux应用程序参数传递的深入探索

Linux应用程序参数传递的深入探索

大家好&#xff0c;今天给大家介绍Linux应用程序参数传递的深入探索&#xff0c;文章末尾附有分享大家一个资料包&#xff0c;差不多150多G。里面学习内容、面经、项目都比较新也比较全&#xff01;可进群免费领取。 在Linux环境中&#xff0c;应用程序的参数传递是一个核心且灵…
阅读更多...
最新文章

Copyright @ 2022~2023