本文是《从0开始图形学》笔记的第五章,初步介绍变换矩阵的作用和求解方式,通过本章内容,我们将掌握模型的旋转和移动。
矩阵的初认识
图形学自然避不开矩阵,矩阵为点坐标的变换提供了一个优雅简洁的处理方案。简单来说,使用矩阵可以对物体的坐标进行旋转和移动提供统一的计算方式。
矩阵的乘法运算法则如下图所示,以图形学用的最多的是4x4的矩阵为例
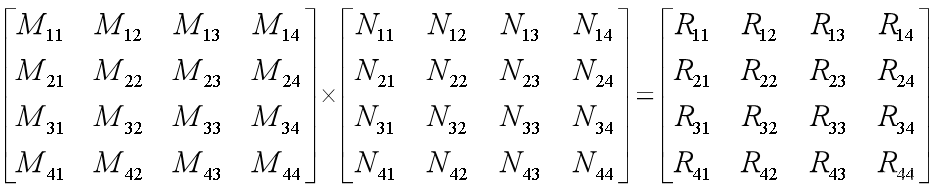
已知矩阵M和N,其乘积为R,则R的第m行第n列元素为M第m行和N中第n列的乘积,例如:
![]()
上面的公式可通过以下直观的感受一下
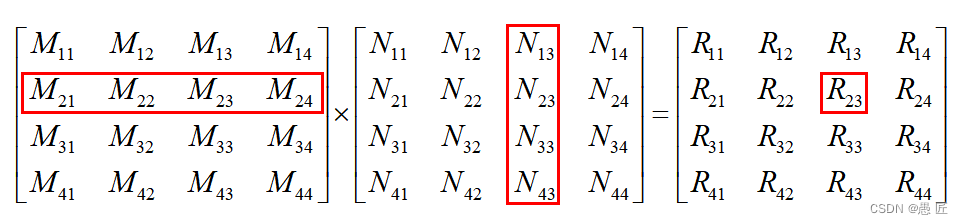
所以,这就必然要求矩阵M的列数和矩阵N的行数要一致,否则无法相乘!那矩阵又是如何作用于点坐标的呢?我们把点坐标中的x,y,z数值排列,并在后面补上1凑成一个4行1列的矩阵,那么使用矩阵左乘它则可以得到一个新的坐表[x1,y1,z1]!
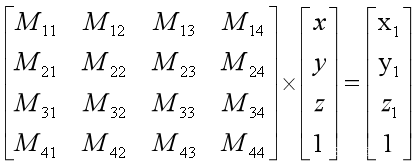
好吧,我已经迫不及待的想展示矩阵的魔力了
首先,定义一个矩阵,这个矩阵的来源将在后面讲到
float matrix[16] =
{0.707107, 0, -0.707107, 131.802,0, 1, 0, 0,0.707107, 0, 0.707107, -318.198,0, 0, 0, 1
};然后,在读入点数据的时候将每个点用矩阵进行旋转
for (int i = 0; i < _ptNum; ++i)
{iF >> _pts[i * 3 + 0] >> _pts[i * 3 + 1] >> _pts[i * 3 + 2];// 对点坐标进行旋转MatrixMultiplyPoint(matrix, &_pts[i * 3]);
}其中的MatrixMultiplyPoint函数中的运算过程就是上述介绍的矩阵乘法
void MatrixMultiplyPoint(float* m, float* p)
{float x, y, z;x = m[0] * p[0] + m[1] * p[1] + m[2] * p[2] + m[3];y = m[4] * p[0] + m[5] * p[1] + m[6] * p[2] + m[7];z = m[8] * p[0] + m[9] * p[1] + m[10] * p[2] + m[11];//p[0] = x;p[1] = y;p[2] = z;
}
效果如下图

我们将模型如愿的进行了旋转!而这一操作仅仅用了16个数而已。
矩阵详解和求法
现在我们已经了解了矩阵的强大,那么要如何求一个矩阵呢?
(1)矩阵的基础拆分
矩阵可以拆分两种常用的基本作用:围绕坐标轴旋转和移动,而实现这两个基本作用的数据分别位于矩阵中的不同部分,如下图所示,红色框内为旋转作用,蓝色框内为移动作用。

两种矩阵的特点有:
(1)两个矩阵最后一行固定为[0 0 0 1];
(2)单围绕坐标轴旋转作用的矩阵中蓝色框部分都为0;
(3)单移动作用的矩阵中红色框部分固定为单位阵;
如下图,左边为单围绕坐标轴旋转的矩阵,右边为单移动的矩阵
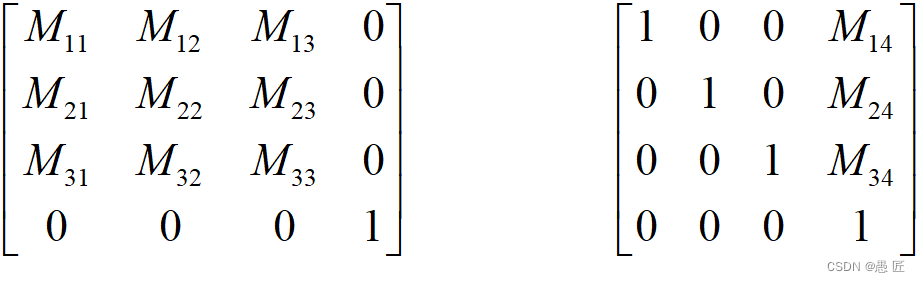
只要有这两种矩阵,那么就可以通过矩阵的乘法不断地累加效果,比如,我要先移动物体,其矩阵为M1,再旋转物体,其矩阵为M2,那么这两个操作的结果为M2xM1(注意:顺序不能颠倒),由前面的讲解我们可以知道M2xM1得到的还是一个4x4的矩阵!因此,我们就可以无穷无尽的进行不断地操作,只要将每次的操作矩阵左乘上当前矩阵即可,最终还是一个4x4的矩阵!所以任何复杂的操作都可以拆成多个上述的两种基础矩阵,再进行累乘得到对应的矩阵。
(2)基础矩阵的求法
那么如何求解这两类基础矩阵呢?这里我们提供一个结果,不展开详细的求解。单围绕坐标轴旋转的矩阵可根据其围绕x轴,y轴,z轴分为3种,依次如下图(假设旋转角度为)

单移动矩阵更简单,假设要对一个模型在三个轴方向上移动(x, y, z),那么它的矩阵就是

这里有一个注意点是刚接触矩阵的人很容易搞不清楚的,矩阵的所有旋转都是以坐标系原点为轴点的,如果想要模型绕着自身的某个坐标(x, y, z)旋转,则需要将模型移动(-x, -y, -z),再旋转,最后再移动(x, y, z)将模型移回原位置!下面我们就以上一节旋转高达模型为例,讲解其矩阵的来源。
第一步:通过遍历所有的点坐标,我们可以知道改模型的中心点大概在(450, 500, 0)的位置上,那么我们就需要将模型移动(-450, -500, 0),将旋转点移到坐标系原点,可得该步骤的矩阵为

第二步:我们将模型绕着Y轴旋转-45°,可得到该步骤的矩阵为

第三部:将旋转后的模型移回原来的位置,可得该步骤矩阵为
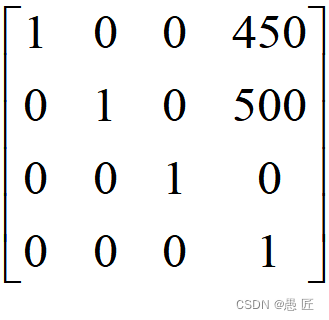
所以我们最后将这3个矩阵进行累乘,即可得到我们最后的结果
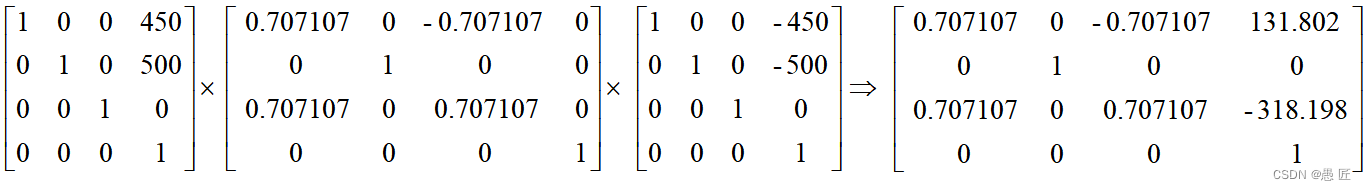
矩阵讲解先告一段落,后续我们还将讲解另外一种矩阵----透视投影矩阵,以及鼠标交互时还会设计矩阵的其他知识,下一章我们将使用纹理贴图给高达模型穿上皮肤。