1. 概率、熵与码字长度

1.1. 数据压缩的目的

1.1.1. 给定一个数据集中的符号，将最短的编码分配给最可能出现的符号

1.2

 

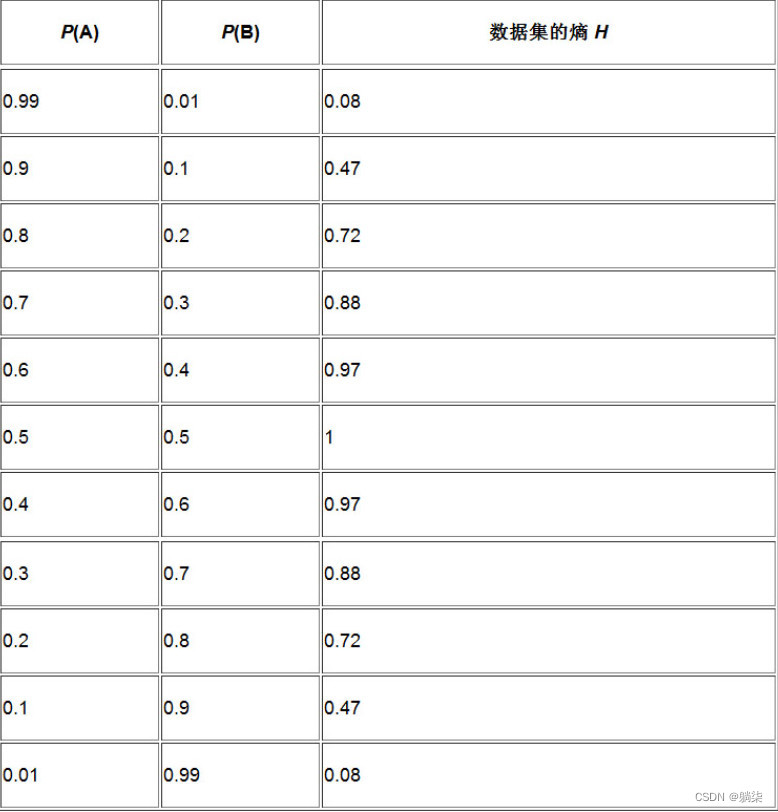
1.2.1. 当P(A)=P(B)，也就是两个符号等可能出现时，数据集对应的熵取最大值LOG2（符号的个数），此时数据集很难压缩

1.2.2. 其中一个符号出现的可能越大，数据集的熵值就越小，此时数据集也越容易压缩

1.2.3. 对只包含两个符号的数据集来说，两个符号互换概率不影响其熵值

1.3. 启示

1.3.1. 随着数据集的冗余度下降，它的熵在变大，其最大值为数据集中不同符号个数的LOG2值

1.3.2. 数据集中一个符号出现的概率越大，整个数据集的熵就越小，数据集也就越容易压缩

1.3.3. 码字的长度与符号的出现概率密切相关，而与符号本身没有太大关系

2. VLC算法

2.1. 在过去的40多年中，人们创造了数百种VLC算法

2.2. 在为数据集选择一种VLC编码方法的考虑因素

2.2.1. 数据集的整体大小

2.2.2. 数据范围

2.2.3. 计算各个符号的出现概率

2.2.4. 如果不这样做，得到的结果可能就是，数据集的大小不但没有压缩，有可能反而比原来的数据集还大

2.3. 存在的主要问题

2.3.1. 它们不按字节 / 字 / 整型对齐

2.3.2. 对于大的数值N，为了方便解码，其码字长度的增长速度一般会超过lb(N)个二进制位

2.3.3. 解码的速度很慢（每次只能读取一个二进制位）

2.3.4. 只能用于表示压缩数据流，没有其他应用

3. 设计VLC集的码字原则

3.1. 越频繁出现的符号，其对应的码字越短

3.2. 码字需满足前缀性质

4. 前缀性质

4.1. 如果一个码字是另一个码字的前缀，那么用VLC解码二进制流就会很难

4.2. 某个码字被分配给一个符号之后，其他的码字就不能用该码字作为前缀

4.2.1. 每个符号都能通过其码字前缀唯一地确定

4.3. 前缀性质是VLC能正常工作所必须具有的性质

4.3.1. 与二进制表示相比，VLC要更长一些

5. 唯一可译码

5.1. uniquely decodable codes

6. 非奇异码

6.1. nonsingular codes

7. 每一种前缀编码都是唯一可译的和非奇异的

8. VLC编码步骤

8.1. 遍历数据集中的所有符号并计算每个符号的出现概率

8.1.1. 画出数据集中所有符号的直方图

8.2. 根据概率为每个符号分配码字，一个符号出现的概率越大，所分配的码字就越短

8.2.1. 根据出现的频数对直方图进行排序

8.2.2. 给每个符号分配一个VLC，从VLC集中码字最短的开始

8.3. 再次遍历数据集，对每一个符号进行编码，并将对应的码字输出到压缩后的数据流中

9. VLC解码步骤

9.1. 由于码字的长度并非是固定的，因此解码过程还是稍微有些复杂

9.2. 解码的时候，我们会一二进制位一二进制位地读取数据，直到读取的二进制位流与其中的某个码字相匹配

9.3. 一旦匹配，就会输出相应的符号，并继续读取下一个码字

10. 摩尔斯码

10.1. 1836年

10.1.1. 画家Samuel F. B. Morse

10.1.2. 物理学家Joseph Henry

10.1.3. 机械师Alfred Vail

10.1.4. 发明了第一套电报系统

10.2. 克劳德•香农

10.2.1. 摩尔斯码方面的专家

10.3. 最简单的编码文本信息的方法

10.3.1. 用数字126来编码AZ的英文字母

10.4. 发送一次信息所需要的人工操作次数太多

10.4.1. 物理硬件（发报机设备）和人工硬件(也就是操作人员的手腕）的磨损比预期的要快，解决方法则是使用统计来减少工作量

10.5. 对符号分配变长编码（variable-length codes，VLC）的最初实现之一

10.6. 为英语字母表中的每一个字符都分配了或长或短的脉冲，一个字母用得越频繁，其编码也就越短、越简单

10.6.1. 目的则在于减少传输信息过程中所需要的总工作量

11. 通用编码

11.1. universal codes

11.2. 一种将整数转换为VLC的独特方法

11.3. 一类特殊的前缀编码

11.4. 为正整数赋上一个长度可变的二进制码字

11.5. 数值越小，其对应的码字也越短

11.5.1. 因为假定小整数比大整数出现得更频繁

12. 二进制编码

12.1. 不满足前缀性质

12.2. 用B(n)来表示整数n的标准二进制表示

12.3. beta编码或二进制编码

12.4. 给定0~N的任意整数，都能用1+floor(lb(n))个二进制位来表示

12.4.1. 只要提前知道N的值，就能通过固定长度表示法来避开前缀问题

12.4.2. 如果不能提前知道数据集中有多少个不同的整数，就不能用固定长度表示法

13. 一元码

13.1. 满足前缀性质

13.2. 任意正整数N，它的一元码表示都是N-1个1后面跟着1个0

13.2.1. 4的一元码表示为1110

13.3. 整数N的一元码长度也是N个二进制位

13.4. 将一元码应用在那些前一个符号的出现概率是后一个符号2倍的数据集上，效果最佳

13.5. 如果每个整数N的出现概率P(N)服从指数分布2^(-N)，即1/2、1/4、1/8、1/16、1/32，其他以此类推，就可以使用一元码进行编码

14. Peter Elias

14.1. 1923年11月23日生

14.2. 1955年，他就引入了卷积码（convolutional codes），作为分组码（block codes）的一种替代方法

14.3. 建立了二进制删除信道（binary erasure channel），并提出了用纠错码的列表译码（list decoding of error-correcting codes）来代替唯一可译码（unique decoding）

14.4. Elias gamma编码

14.4.1. 用于事先无法确定其上界的整数的编码

14.4.1.1. 不知道最大的整数会是多大

14.4.2. 对整数n的出现概率P(n)=1/(2n*n)的情形比较适用

14.4.3. 最主要的思想是不再对整数直接编码，而是用其数量级作为前缀

14.4.3.1. 相应的码字就由两部分组成，即与此整数相当的2的次幂再加上余数

14.4.4. 工作原理

14.4.4.1. 找出最大的整数N，使其满足2^N＜n＜2^(N+1)，并且将n表示为n=2^N+L这样的形式

14.4.4.1.1. L=n-2^N

14.4.4.1.2. n=12,2^3=8,2^4=16,2^3＜n＜2^4,N=3

14.4.4.1.3. L=12-2^3=4

14.4.4.2. 用一元码表示N

14.4.4.2.1. N=3,一元码110

14.4.4.3. 将L表示为长为N的二进制编码，并加在步骤(2)中得出的一元码之后

14.4.4.3.1. 有了这样的对称性，后面才能顺利解码

14.4.4.3.2. L=4，其对应的长度为3的二进制码为100

14.4.4.3.3. 将前两个步骤得出的编码连接，就得到了最终的输出110100

14.5. Elias delta编码

14.5.1. 对整数N的出现概率P(N)等于1/[2n(lb(2n)*lb(2n))的数据集来说是理想的选择

14.5.2. 工作原理

14.5.2.1. 将要编码的数N用二进制表示

14.5.2.1.1. 将N=12表示为二进制1100

14.5.2.2. 数一下N的二进制位数，并将这个位数转化为二进制，作为C

14.5.2.2.1. 12的二进制表示共有4位，将4表示为二进制，即C = 100

14.5.2.3. 去掉N的二进制表示的最左边一位，这个值肯定是1

14.5.2.3.1. 去掉N=12的二进制表示的最左一位，得到100

14.5.2.4. 将C的二进制表示加在去掉最左边一位后的N的二进制表示之前

14.5.2.4.1. 将C = 100加到上一步骤所得的结果之前，得到100100

14.5.2.5. 在上一步骤所得的结果前加上C的二进制位数减1个0作为最终的编码

14.5.2.5.1. 将C的二进制位数减1，即3-1 = 2，在上一步骤所得的结果前加上2个0，由此得到12的最终编码为00100100

15. 谷歌的Varint算法

15.1. 最基本的概念早在1972年就提出

15.2. 2010年作为“避免压缩整数”（escaping for compressed integers）而被重新引入

15.3. 是一种表示整数的方法，它用一个或多个字节来表示一个整数，数值越小用的字节数越少，数值越大用的字节数越多

15.3.1. 结合了VLC的灵活性和现代计算机体系结构的高效率，是一种很好的混合方法

15.3.2. 既允许我们表示可变范围内的整数，同时还对自身的数据进行了对齐以提高解码的效率，达到了双赢

15.4. 方法

15.4.1. 将几个字节连接起来表示整数

15.4.2. 并用每个字节的MSB作为布尔标志，来判断当前的字节是否为该整数的最后一个字节

15.4.3. 每个字节的低7位则用来存储该数的二进制补码（two's complement representation）

15.4.4. 整数1可以用一个字节表示，因此它的MSB不需要设置，可表示为00000001

15.5. 示例

15.5.1. 10101100 00000010

15.5.1.1. 10101100 00000010 → 0101100 0000010

15.5.1.1.1. 删掉每个字节的MSB

15.5.1.1.1.1. 它的作用只是判断当前字节是否是最后一个字节

15.5.1.1.1.2. 第一个字节的MSB已经设置为1，因为用Varint方法来表示，该数需要多个字节

15.5.1.2. 0101100 0000010

15.5.1.2.1. 将剩下的两个7二进制位的数据顺序颠倒一下

15.5.1.2.1.1. 用Varint方法表示时，低位的字节在前

15.5.1.3. 0000010 0101100

15.5.1.3.1. 将二进制表示转换为十进制数，就得到了最终的数值300