1130. 叶值的最小代价生成树
难度中等272
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有
0个或是2个子节点。 - 数组
arr中的值与树的中序遍历中每个叶节点的值一一对应。 - 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
如果一个节点有 0 个子节点,那么该节点为叶节点。
示例 1:
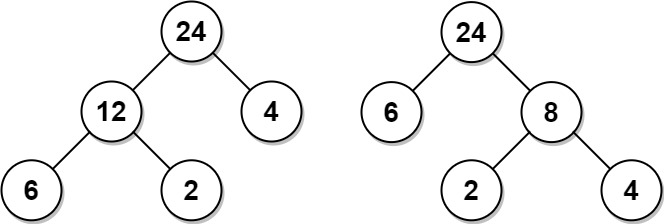
输入:arr = [6,2,4]
输出:32
解释:有两种可能的树,第一种的非叶节点的总和为 36 ,第二种非叶节点的总和为 32 。
示例 2:
输入:arr = [4,11]
输出:44
提示:
2 <= arr.length <= 401 <= arr[i] <= 15- 答案保证是一个 32 位带符号整数,即小于
231。
贪心
class Solution {public int mctFromLeafValues(int[] arr) {// 哈夫曼树 : 每次选择两个值最小的进行合并List<Integer> list = new ArrayList<>();for(int i = 0; i < arr.length; i++){list.add(arr[i]);}int ans = 0;while(list.size() > 1){int i = 1;int mul = Integer.MAX_VALUE, tmp = 1;while(i < list.size()){if(mul > list.get(i) * list.get(i-1)){mul = list.get(i) * list.get(i-1);tmp = i;}i += 1;}// 答案加上当前最小乘积,并删除两个数中较小的节点ans += mul;if(list.get(tmp) > list.get(tmp-1)) list.remove(tmp-1);else list.remove(tmp);}return ans;}
}
记忆化搜索 ==> 动态规划
打开思路的几个关键点:
1、对于每个区间[L, R]的叶子结点,最终会汇聚成一个根节点,但这个根节点会根据[L, R]中的子区间划分方式的不同而不同,我们要做的就是要求其中的最小的
2、不要纠结“树的形状”、“树有几层”等等的关于“树”相关的东西,区间划分一旦定了,树就定了,我们需要将“树”的概念抽象掉,唯一核心的就是一个区间对应2个子树和一个根节点!!!
3、对于任意一个区间[L, R],一定是将其划分成2个区间,分别对应最终根节点的左右子树。而根节点的值就是两个区间各自的最大值乘积。
4、对于根节点的子树中非叶子结点的累加值,其实就是在递归子问题中求得了(也可以认为是状态转移方程,因为记忆化搜索和DP本来就是一一对应的)
https://leetcode.cn/problems/minimum-cost-tree-from-leaf-values/solution/qu-jian-dp-dong-tai-gui-hua-die-dai-xie-g4jac/
class Solution {public int mctFromLeafValues(int[] arr) {//区间dp://先计算每个区间内的最大值,用于计算每个非叶子节点的值//分成左右两个子树,得到两个子树中的非叶子节点的和的最小值,相加再加上当前树的root结点的值(上面得到的每个区间的最大值可以计算得到)int n = arr.length;// 预处理区间最大值,这样可以O(1) 的获取每个区间的最大值int[][] g = new int[n][n];for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)for(int k = i; k <= j; k++)g[i][j] = Math.max(g[i][j], arr[k]);int[][] f = new int[n][n];// 区间DPfor(int len = 1; len <= n; len++){ // 枚举区间长度for(int i = 0; i + len - 1 < n; i++){ // 枚举区间起点int j = i + len - 1; // 区间终点f[i][j] = Integer.MAX_VALUE; // 因为求区间最小值,初始化为infif(len == 1) f[i][j] = 0;else{for(int k = i; k < j; k++)f[i][j] = Math.min(f[i][j], f[i][k] + f[k+1][j] + g[i][k] * g[k+1][j]);}}}return f[0][n-1];}
}
单调栈
https://leetcode.cn/problems/minimum-cost-tree-from-leaf-values/solution/1130-cchao-100de-dan-diao-zhan-tan-xin-j-7zwh/
贪心的单调栈解法
- 最优情况:其实就是严格有序的,从小到大来乘然后累加,对应情况就是类似[4,3,2,1]
- 指导原则:严格按照arr的顺序下,每次总是用乘积最小两个数一起乘
- 使用一个单调递减的栈来实现局部有序
- 不满足有序:一旦发现当前元素大于栈顶,则弹出栈顶元素,(这个元素作为叶子节点,必须要做乘法)
- 此时需要考虑是新的栈顶 和 当前元素 的最小值 去乘,乘的结果会做累加
- 弹出全部比它小的元素后,插入新的元素到栈顶
- 坑:最后栈里可能存有排序好的数字(本质就是最优的解),需要依次弹出一个并累加乘积
- 整个过程中累加结果就是结果+
class Solution {public int mctFromLeafValues(int[] arr) {// 维护一个单调递减的栈Deque<Integer> dq = new ArrayDeque<>();// 预先插入一个极大值,后续无需判断边缘情况,如s为空dq.addLast(Integer.MAX_VALUE);int n = arr.length;int res = 0;for(int num : arr){while(num > dq.peekLast()){int cur = dq.pollLast();// 这里要考虑可能接下来栈顶数字比arr[i]还要小,我们需要用这个更小数字来乘res += cur * Math.min(dq.peekLast(), num);}dq.addLast(num);}// 最后弹出剩余元素(除了预先插入 INT_MAX,所以最小是3才考虑)while(dq.size() >= 3){int cur = dq.pollLast();res += cur * dq.peekLast();}return res;}
}