目录
平移
示例代码:
齐次坐标矢量的最后一个分量w
旋转
p的坐标,可得等式 R1:
使用r、α、β来表示点p'的坐标,可得等式 R2:
利用三角函数两角和公式,可得等式 R3:
最后,将p的坐标等式代入上式,消除r和α,可得等式 R4:
三角函数两角和公式
示例代码:
平移
考虑一下,为了平移一个三角形,你需要对它的每一个顶点做怎样的操作?答案是,你需要对顶点坐标的每个分量(x和y),加上三角形在对应轴(如X轴或Y轴)上平移的距离。比如,将点p(x,y,z)平移到p' (x',y',z'),在X轴、Y轴、Z轴三个方向上平移的距离分别为Tx,Ty,Tz,其中Tz为0。
那么在坐标的对应分量上,直接加上这些T值,就可以确定p'的坐标了
x'=x+Tx
y'=y+Ty
z'=z+Tz
如图所示:

我们只需要着色器中为顶点坐标的每个分量加上一个常量就可以实现上面的等式。显然,这是一个逐顶点操作(per-vertex operation)而非逐片元操作,上述修改应当发生在顶点着色器,而不是片元着色器中。
xyz 各移动 0.5 0.5 0

示例代码:
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'uniform vec4 u_Translation;\n' +'void main() {\n' +' gl_Position = a_Position + u_Translation;\n' +'}\n';var FSHADER_SOURCE ='void main() {\n' +' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +'}\n';// x y z 各移动 0.5 0.5 0
var Tx = 0.5, Ty = 0.5, Tz = 0.0;function main() {var canvas = document.getElementById('webgl');var gl = getWebGLContext(canvas);if (!gl) {console.log('Failed to get the rendering context for WebGL');return;}if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {console.log('Failed to intialize shaders.');return;}var n = initVertexBuffers(gl);if (n < 0) {console.log('Failed to set the positions of the vertices');return;}var u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');if (!u_Translation) {console.log('Failed to get the storage location of u_Translation');return;}gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0); // 这里第四个分量必须是 0.0gl.clearColor(0, 0, 0, 1);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, n);
}function initVertexBuffers(gl) {var vertices = new Float32Array([0, 0.5, -0.5, -0.5, 0.5, -0.5]);var n = 3; // The number of verticesvar vertexBuffer = gl.createBuffer();if (!vertexBuffer) {console.log('Failed to create the buffer object');return -1;}gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);var a_Position = gl.getAttribLocation(gl.program, 'a_Position');if (a_Position < 0) {console.log('Failed to get the storage location of a_Position');return -1;}gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);gl.enableVertexAttribArray(a_Position);return n;
}
首先,main()函数中定义了等式3.1中三角形在各轴方向上的平移距离:

因为Tx、Ty、Tz对于所有顶点来说是固定(一致)的,所以我们使用uniform变量u_Translation来表示三角形的平移距离。首先,获取uniform变量的存储位置:
![]() 然后将数据传给着色器:
然后将数据传给着色器:

注意,gl.uniform4f()函数需接收齐次坐标,所以我们把最后一个参数被设为0.0。这么做的具体原因将在稍后讨论。
现在来看一下修改后的顶点着色器:我们新定义了uniform变量u_Translation,用来接收了三角形在各轴方向上的平移距离。该变量的类型是vec4,这样它就可以与vec4类型的顶点坐标a_Position直接相加,然后赋值给同样是vec4类型的gl_Position。记住,GLSL ES中的赋值操作只能发生在相同类型的变量之间。

在做完准备工作之后,我们就直奔主题:在顶点着色器中,按照上述等式,为a_Position变量的每个分量(x,y,z)加上u_Translation变量中对应方向的平移距离(Tx,Ty,Tz),并赋值给gl_Position。
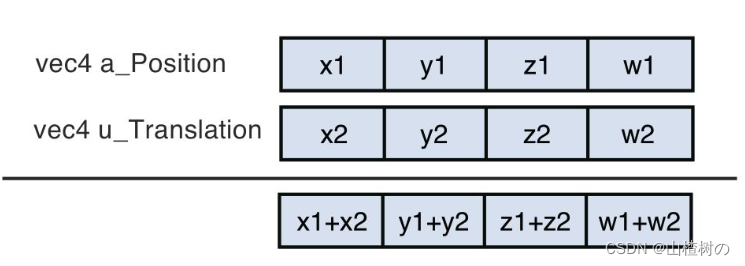
因为a_Position和u_Translation变量都是vec4类型的,所以你可以直接使用+号,两个的矢量的对应分量会被同时相加,如下图所示。方便的矢量相加运算是GLSL ES提供的特性之一。
齐次坐标矢量的最后一个分量w
最后,来解释一下齐次坐标矢量的最后一个分量w。gl_Position是齐次坐标,具有4个分量。如果齐次坐标的最后一个分量是1.0,那么它的前三个分量就可以表示一个点的三维坐标。在本例中,如上图所示,平移后点坐标第4分量w1+w2必须是1.0 (因为点的位置坐标平移之后还是一个点位置坐标),而w1是1.0(它是平移前点坐标第4分量),所以平移矢量本身的第4分量w2只能是0.0,这就是为什么gl.uniform4f()的最后一个参数为0.0。
最后,调用gl.drawArrays(gl.TRIANGLES,0,n)执行顶点着色器,每次执行都会进行以下3步:
1.将顶点坐标传给a_Position;
2.向a_Position加上u_Translation;
3.结果赋值给gl_Position。
一旦顶点着色器执行完毕,目的就达到了:每个顶点在同一个方向上平移了相同的距离,整个图形(本例中为三角形)也就被平移了。
旋转
旋转比平移稍微复杂一些,因为描述一个旋转本身就比描述一个平移复杂。为了描述一个旋转,你必须指明:
● 旋转轴(图形将围绕旋转轴旋转)。
● 旋转方向(方向:顺时针或逆时针)。
● 旋转角度(图形旋转经过的角度)。
本文这样来表述旋转操作:绕Z轴,逆时针旋转了β角度。这种表述方式同样适用于绕X轴和Y轴的情况。
在旋转中,关于“逆时针”的约定是:如果β是正值,观察者在Z轴正半轴某处,视线沿着Z轴负方向进行观察,那么看到的物体就是逆时针旋转的,如下图所示。这种情况又可称作正旋转(positive rotation)。我们也可以使用右手来确认旋转方向(正如右手坐标系一样):右手握拳,大拇指伸直并使其指向旋转轴的正方向,那么右手其余几个手指就指明了旋转的方向,因此正旋转又可以称为右手法则旋转(right-hand-rule rotation)。

上面我们计算了平移的数学表达式,现在来看旋转的数学表达式。根据下图,假设点p(x,y,z)旋转β角度之后变为了点p'(x',y',z'):首先旋转是绕Z轴进行的,所以z坐标不会变,可以直接忽略;然后,x坐标和y坐标的情况有一些复杂。

上图中,r是从原点到点p的距离,而α是X轴旋转到点p的角度。用这两个变量计算出点p的坐标,转换等式如下。
p的坐标,可得等式 R1:
x = r cosα
y = r sinα
使用r、α、β来表示点p'的坐标,可得等式 R2:
x' = r cos(α + β)
y' = r sin(α + β)
利用三角函数两角和公式,可得等式 R3:
x' = r (cosα cosβ - sinα sinβ)
y' = r (sinα cosβ + cosα sinβ)
最后,将p的坐标等式代入上式,消除r和α,可得等式 R4:
x' = x cosβ - y sinβ
y' = x sinβ + y cosβ
z' = z
三角函数两角和公式
- sin(a+b) = sina cosb + cosa sinb
- sin(a-b) = sina cosb - cosa sinb
- cos(a+b) = cos cosb - sina sinb
- cos(a-b) = cosa cosb + sina sinb
我们可以把sinβ和cosβ的值传给顶点着色器,然后在着色器中根据等式R4计算旋转后的点坐标,就可以实现旋转这个点的效果了。使用JavaScript内置的Math对象的sin()和cos()方法来进行三角函数运算。
下图显示了下面示例代码的运行结果,可见,三角形绕Z轴逆时针旋转了90度。

示例代码:
旋转代码,其结构与上面平移很像,只不过顶点着色器中进行的是旋转而不是平移操作。片元着色器和平移中完全相同,我们将它省略了。此外,为了配合顶点着色器的改动,main()函数也有几处改动。注意顶点着色器中实现了等式R4。
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'uniform float u_CosB, u_SinB;\n' +'void main() {\n' +/* 下面两行为拓展,旋转的同时再平移 */// ' gl_Position.x = (a_Position.x * u_CosB - a_Position.y * u_SinB) + u_move.x;\n' +// ' gl_Position.y = (a_Position.x * u_SinB + a_Position.y * u_CosB) + u_move.y;\n' +' gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;\n' +' gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;\n' +' gl_Position.z = a_Position.z;\n' +' gl_Position.w = 1.0;\n' +'}\n';var FSHADER_SOURCE ='void main() {\n' +' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +'}\n';// 旋转90度
var ANGLE = 90.0; function main() {// Retrieve <canvas> elementvar canvas = document.getElementById('webgl');var gl = getWebGLContext(canvas);if (!gl) {console.log('Failed to get the rendering context for WebGL');return;}if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {console.log('Failed to intialize shaders.');return;}var n = initVertexBuffers(gl);if (n < 0) {console.log('Failed to set the positions of the vertices');return;}var radian = Math.PI * ANGLE / 180.0; // 转换为弧度var cosB = Math.cos(radian);var sinB = Math.sin(radian);var u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');var u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');// var u_move = gl.getUniformLocation(gl.program, 'u_move');if (!u_CosB || !u_SinB) {console.log('Failed to get the storage location of u_CosB or u_SinB');return;}gl.uniform1f(u_CosB, cosB);gl.uniform1f(u_SinB, sinB);// gl.uniform3f(u_move, 0.5, 0.5, 0);gl.clearColor(0, 0, 0, 1);gl.clear(gl.COLOR_BUFFER_BIT);gl.drawArrays(gl.TRIANGLES, 0, n);
}function initVertexBuffers(gl) {var vertices = new Float32Array([0, 0.5, -0.5, -0.5, 0.5, -0.5]);var n = 3; // The number of verticesvar vertexBuffer = gl.createBuffer();if (!vertexBuffer) {console.log('Failed to create the buffer object');return -1;}gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);var a_Position = gl.getAttribLocation(gl.program, 'a_Position');if (a_Position < 0) {console.log('Failed to get the storage location of a_Position');return -1;}gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);gl.enableVertexAttribArray(a_Position);return n;
}
由于目的是为了将三角形旋转90度,我们得事先计算90度的正弦值和余弦值。在JavaScript中算出这两个值,再传给顶点着色器的两个uniform变量。
你也可以将旋转的角度传入顶点着色器,并在着色器中计算正弦值和余弦值。但是,实际上所有顶点旋转的角度都是一样的,在JavaScript中算好正弦值和余弦值,然后再传递进去,只需要计算一次,效率更高。
上面进行平移变换时,齐次坐标的x、y、z、w分量是作为整体进行加法运算的;而进行旋转变换时,为了计算等式R4,需要单独访问a_Position的每个分量。我们使用点操作符“.”来访问分量,如a_Position.x、a_Position.y或a_Position.z(如下图所示)。

同样,也可以用点操作符向数组的分量赋值访问gl_Position分量,并写入变换后的点坐标分量值。比如,按照等式3.3进行计算x'=xcosβ-ysinβ并赋值给gl_Position的x分量:
![]()
相似地,可以如下计算y':
![]()
根据等式R4,还需要将z原封不动地赋给z',以及将最后一个w分量设为1.0

现在来看一下JavaScript代码中的main()函数:它和平移代码中几乎完全一样,唯一的不同之处就是,本例向顶点着色器传入了cosβ和sinβ值(而非平移距离Tx等)。我们使用JavaScript内置的Math.sin()和Math.cos()函数来计算β的正弦和余弦值。但是,这两个方法必须接受弧度制(而不是角度制)的参数,所以我们还得先把β值从角度制转为弧度制:将角度值90乘以π然后除以180,访问Math.PI可以获得π的值。
![]()
在程序中,我们首先计算旋转角β的弧度值,然后计算sinβ和cosβ的值,最后将结果传入顶点着色器。
如果你觉得示例程序的实现(使用两个uniform变量分别接收cosβ和sinβ)效率不是最优的,你也可以将这两个值作为一个数组传入着色器。比如,你可以这样定义uniform变量:
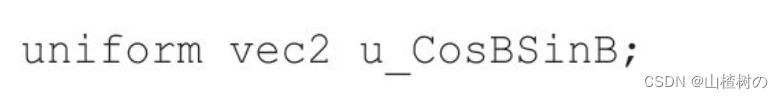
然后这样传入cosβ和sinβ的值:

这样,在顶点着色器中,就可以使用u_CosBSinB.x和u_CosBSinB.y来获取cosβ和sinβ的值。