LeetCode700. 二叉搜索树中的搜索

700. 二叉搜索树中的搜索

文章目录

- - [700. 二叉搜索树中的搜索](https://leetcode.cn/problems/search-in-a-binary-search-tree/)
  - - 一、题目
    - 二、题解
    - - 方法一：迭代
      - 方法二：递归
    - 带main函数测试用例

一、题目

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

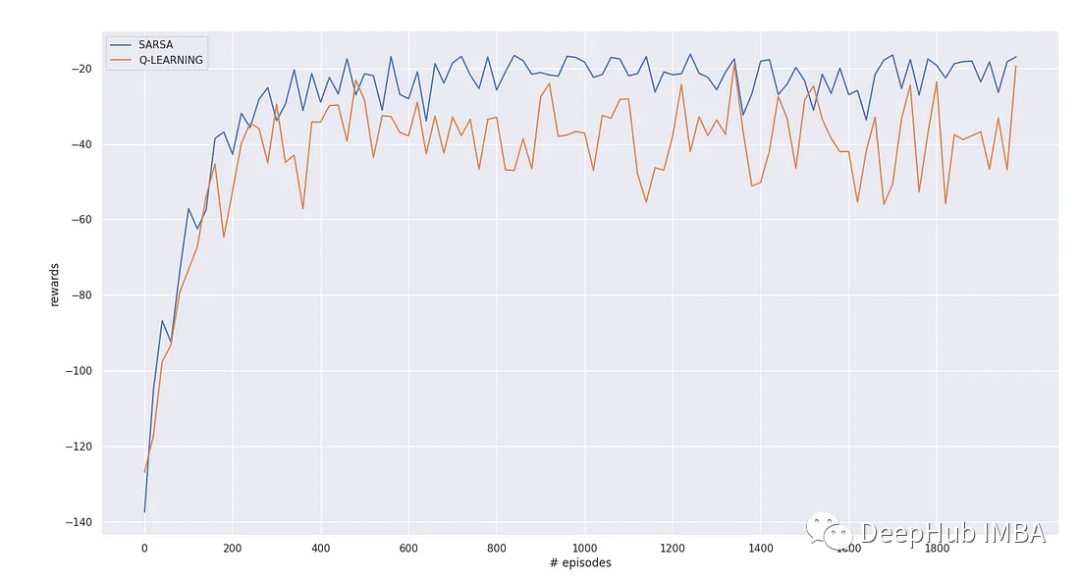
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

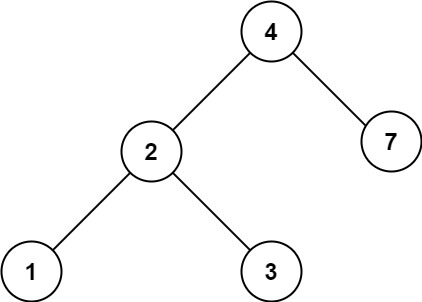
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107

二、题解

方法一：迭代

首先要理解题目的要求：给定一个二叉搜索树（BST）和一个整数值，要求在这个BST中找到值等于给定整数的节点，并返回以该节点为根的子树。如果节点不存在，则返回 null。为了解决这个问题，我们可以分为以下几个步骤：

算法思路：

首先，我们需要明确二叉搜索树的性质：对于任意节点，其左子树的所有节点值都小于它，右子树的所有节点值都大于它。这个性质使得我们可以在搜索过程中有效地缩小搜索范围。
我们从根节点开始，进行迭代搜索。首先，我们初始化一个指针 node 指向根节点。
在迭代过程中，我们不断比较当前节点的值与给定值 val 的大小关系：
- 如果当前节点的值等于 val，那么就找到了目标节点，直接返回该节点。
- 如果当前节点的值小于 val，说明目标节点可能在当前节点的右子树中，因此更新 node 为当前节点的右子节点。
- 如果当前节点的值大于 val，说明目标节点可能在当前节点的左子树中，因此更新 node 为当前节点的左子节点。
重复步骤 3，直到找到目标节点或者搜索范围为空（即 node 为空），此时返回 null 表示没有找到目标节点。

具体实现：

class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if(root == nullptr) return nullptr; // 如果根节点为空，直接返回 nullptrTreeNode *node = root; // 初始化指针 node 指向根节点while(node != nullptr){if(node->val == val){ // 当前节点的值等于目标值，直接返回该节点return node;}else if(node->val < val){ // 当前节点的值小于目标值，更新 node 为右子节点node = node->right;}else{ // 当前节点的值大于目标值，更新 node 为左子节点node = node->left;}}return node; // 返回找到的节点，或者返回 nullptr（没有找到）}
};

算法分析：

时间复杂度：在最坏情况下，我们需要遍历整棵树，时间复杂度为 O(n)，其中 n 是树中节点的个数。但由于是二叉搜索树，平均情况下，搜索范围会逐步缩小，期望时间复杂度更接近 O(log n)。
空间复杂度：由于只使用了常数级别的额外空间来存储指针，空间复杂度为 O(1)。

方法二：递归

算法思路：

首先，我们对根节点进行判空，如果根节点为空，直接返回 nullptr，表示没有找到目标节点。
然后，我们判断当前根节点的值与目标值 val 的关系：
- 如果当前根节点的值等于 val，说明已经找到目标节点，直接返回该根节点。
- 如果当前根节点的值小于 val，说明目标节点可能在右子树中，因此递归调用 searchBST(root->right, val)，在右子树中继续搜索。
- 如果当前根节点的值大于 val，说明目标节点可能在左子树中，因此递归调用 searchBST(root->left, val)，在左子树中继续搜索。
递归继续执行上述步骤，直到找到目标节点或者遍历到叶子节点为止。如果遍历到叶子节点仍然没有找到目标节点，则返回 nullptr。

具体实现：

class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == nullptr) return nullptr; // 如果根节点为空，直接返回 nullptrif (root->val == val) return root; // 当前根节点的值等于目标值，返回该根节点if (root->val < val) {return searchBST(root->right, val); // 在右子树中继续搜索} else {return searchBST(root->left, val); // 在左子树中继续搜索}}
};

算法分析：

时间复杂度：在最坏情况下，我们需要遍历整棵树，时间复杂度为 O(n)，其中 n 是树中节点的个数。但由于是二叉搜索树，平均情况下，搜索范围会逐步缩小，期望时间复杂度更接近 O(log n)。
空间复杂度：由于使用递归调用，系统需要维护递归调用栈，空间复杂度取决于递归深度。在平均情况下，空间复杂度为 O(log n)，在最坏情况下，即树高为 n 时，空间复杂度为 O(n)。

带main函数测试用例

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (!root) return nullptr; // 根节点为空，直接返回 nullptrif (root->val == val) return root; // 当前根节点的值等于目标值，返回该根节点return root->val < val ? searchBST(root->right, val) : searchBST(root->left, val);}
};int main() {// 构建测试用例TreeNode* root = new TreeNode(4);root->left = new TreeNode(2);root->right = new TreeNode(7);root->left->left = new TreeNode(1);root->left->right = new TreeNode(3);int target = 2;Solution solution;TreeNode* result = solution.searchBST(root, target);std::vector<int> output;// 遍历得到的子树节点，将值存入输出向量中std::vector<TreeNode*> stack;TreeNode* current = result;while (current || !stack.empty()) {while (current) {stack.push_back(current);current = current->left;}current = stack.back();stack.pop_back();output.push_back(current->val);current = current->right;}// 输出结果for (int val : output) {std::cout << val << " ";}std::cout << std::endl;// 释放内存（实际情况中可能需要编写更详细的内存释放逻辑）delete root->left->right;delete root->left->left;delete root->left;delete root->right;delete root;return 0;
}