描述
输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构)
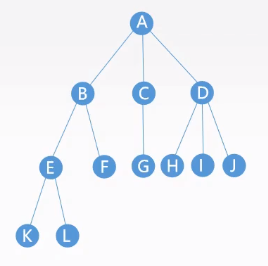
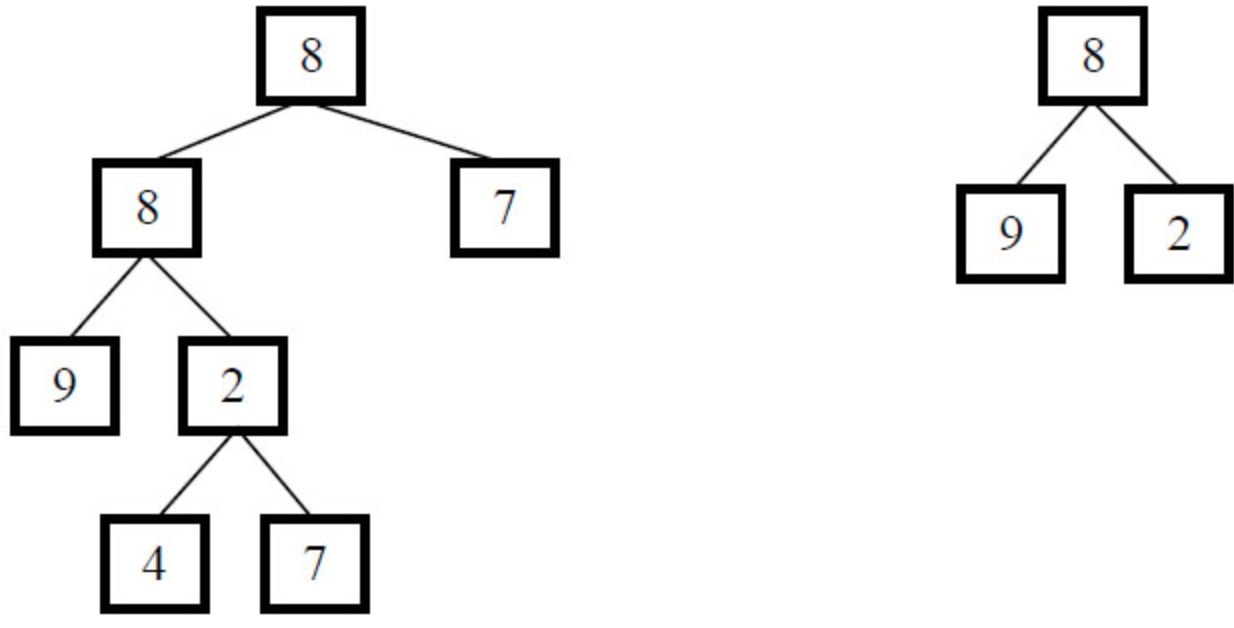
假如给定A为{8,8,7,9,2,#,#,#,#,4,7},B为{8,9,2},2个树的结构如下,可以看出B是A的子结构
数据范围:
0 <= A的节点个数 <= 10000
0 <= B的节点个数 <= 10000
示例1
输入:{8,8,7,9,2,#,#,#,#,4,7},{8,9,2}
返回值:true
示例2
输入:{1,2,3,4,5},{2,4}
返回值:true
示例3
输入:{1,2,3},{3,1}
返回值:false
思路:
按照树 A 中每个节点的遍历顺序比较当前节点和 B 的根节点是否相同,如果相同就按照 B 的结构遍历他们的每个节点。
例子是题目所给的样例:
| 1 2 |
|
1.两个节点都是 8 ,根节点相同,开始遍历其他节点。
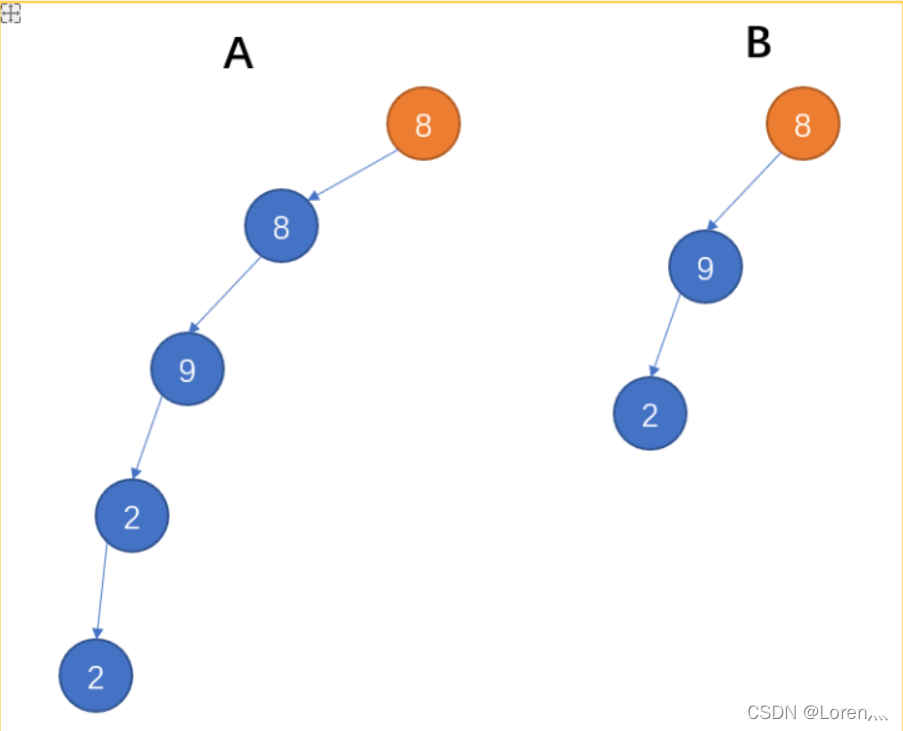
2. 第二个节点不相同函数结束
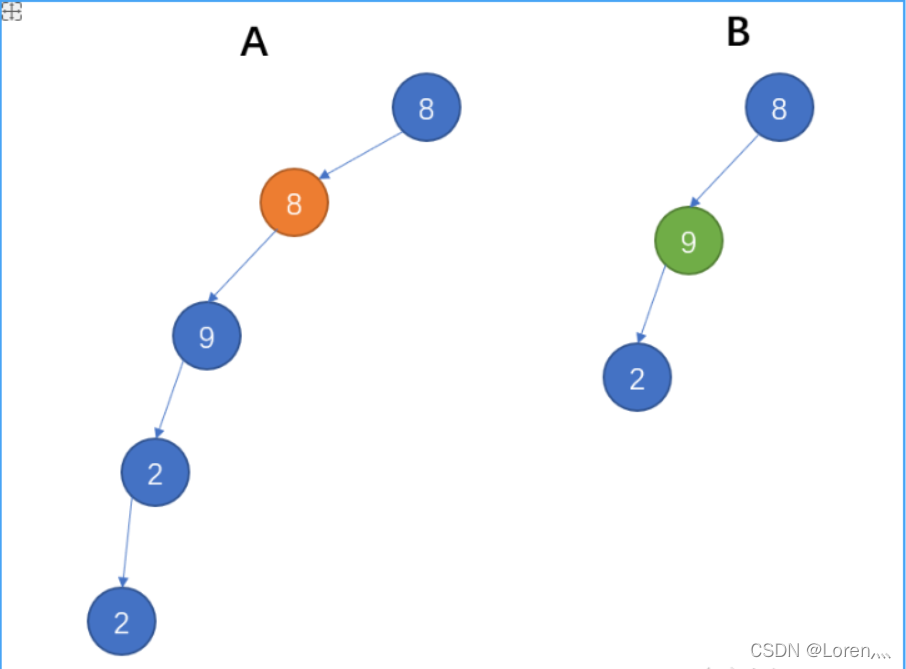
3. 继续比较 A 中节点和 B 的根节点,再次发现相同
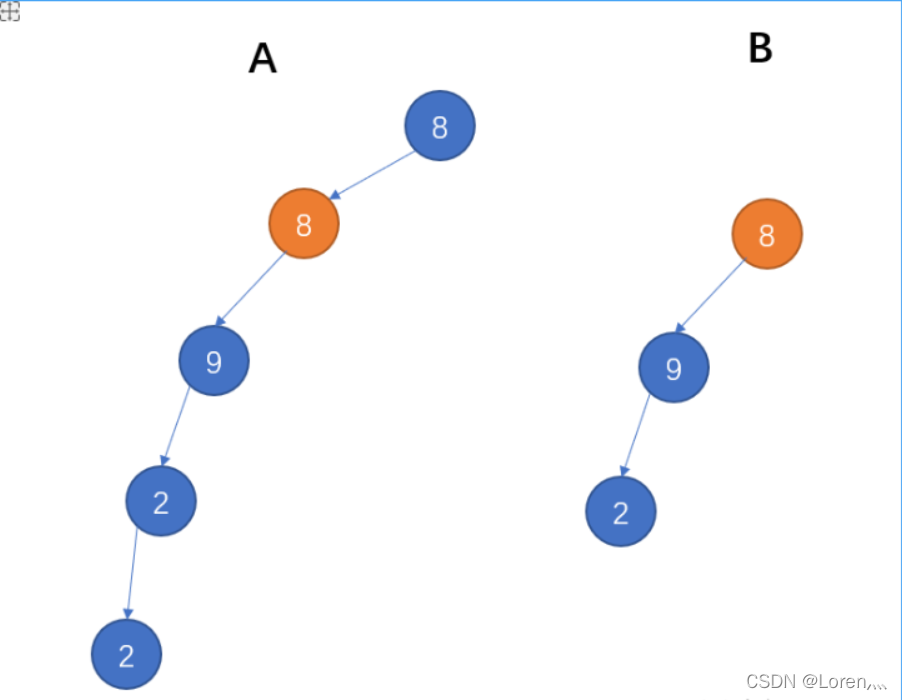
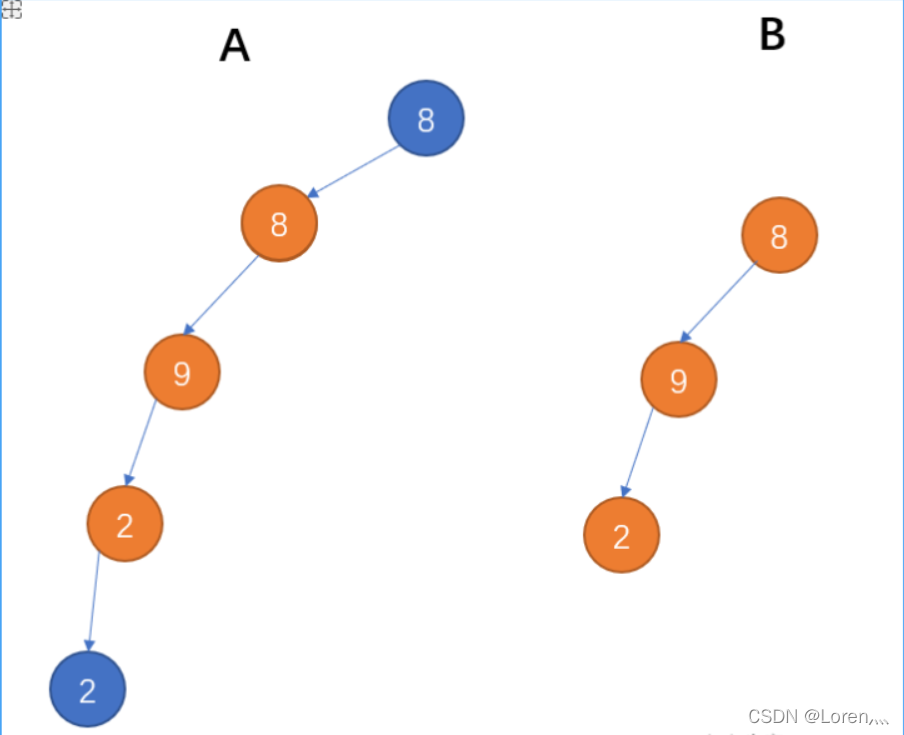
4. 按照 B 的顺序遍历所有节点发现 B 是 A 的子树
复杂度分析
在最坏情况下, 把 A 遍历了一遍,并且对于每个根节点都把 B 遍历了一遍,假设 A 和 B 分别有 m, n 个节点, 所以最坏的时间复杂度是 O(m * n)。
/*
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};*/
class Solution {
public:bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {if(pRoot1 == nullptr || pRoot2 == nullptr) return false;bool flag = false;flag = Istreeboy(pRoot1, pRoot2);if(!flag) flag = HasSubtree(pRoot1->left, pRoot2);if(!flag) flag = HasSubtree(pRoot1->right, pRoot2);return flag;}bool Istreeboy(TreeNode* p1, TreeNode* p2){if(!p2) return true;if(!p1) return false;if(p1->val == p2->val){return Istreeboy(p1->left, p2->left) && Istreeboy(p1->right, p2->right);}return false;}
};