树:
n个结点组成的有限集合。
(1)有且仅有一个特定的称为根的结点。
(2)当n>1时,其余结点可分为m个互不相交的有限集合,其中每个集合本身又是一棵树,称为根节点的子树。
注意:n个结点的树中只有n-1条边。除根节点外,每个结点都有一个前驱边,因此n个结点的树中n-1条边。
树的基本概念:
祖先结点和子孙结点
双亲结点和孩子结点
兄弟节点
度:树中一个结点的子结点的个数称为该结点的度。结点的度即为它孩子结点的个数。
树的度:所有结点的最大度数。
度大于0的结点称为分支结点(存在分支结点)。
度为0的结点称为叶子结点。
结点的层次:即结点存在多少层
结点的高度:从叶子结点开始(从下往上)
结点深度:从根结点开始(从上往下)
树的高度(深度)是树中结点的最大层数。
有序树和无序树:即兄弟结点的不同位置如果是不同的树,则是有序树;如果是同一个树,则是无序树。
路径:树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的(不包含边)。
树中的分支是有向的,即从双亲结点指向孩子结点,所以路径一定是自上而下的。
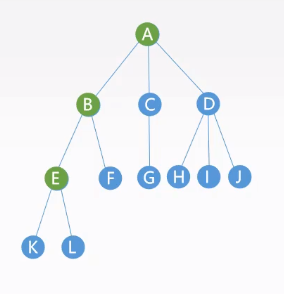
路径为(A->B->E)是有向路径。
路径长度:路径所经历边的个数。上述路径边个数为2。
森林:m棵互不相交的树的集合。
森林通过添加一个根结点可以变为树;树去掉一个根可以变为森林。
森林:

树:
树的性质:
(1)树的结点数等于所有结点的度数加1。
(2)度为m的树中第i层至多有 m i − 1 m^{i-1} mi−1个(i>=1)
(3)高度为h的m叉树至多有( m h m^h mh-1)/(m-1)个结点。
(4)具有n个结点的m叉树的最小高度为[ l o g m n ( m − 1 ) + 1 log_m{n(m-1)+1} logmn(m−1)+1]。
上述结果如下求出:
( m h m^h mh-1)/(m-1) = n从而推出h=[ l o g m n ( m − 1 ) + 1 log_m{n(m-1)+1} logmn(m−1)+1]。
树的结构-树的各种定义及性质
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://xiahunao.cn/news/351269.html
如若内容造成侵权/违法违规/事实不符,请联系瞎胡闹网进行投诉反馈,一经查实,立即删除!相关文章
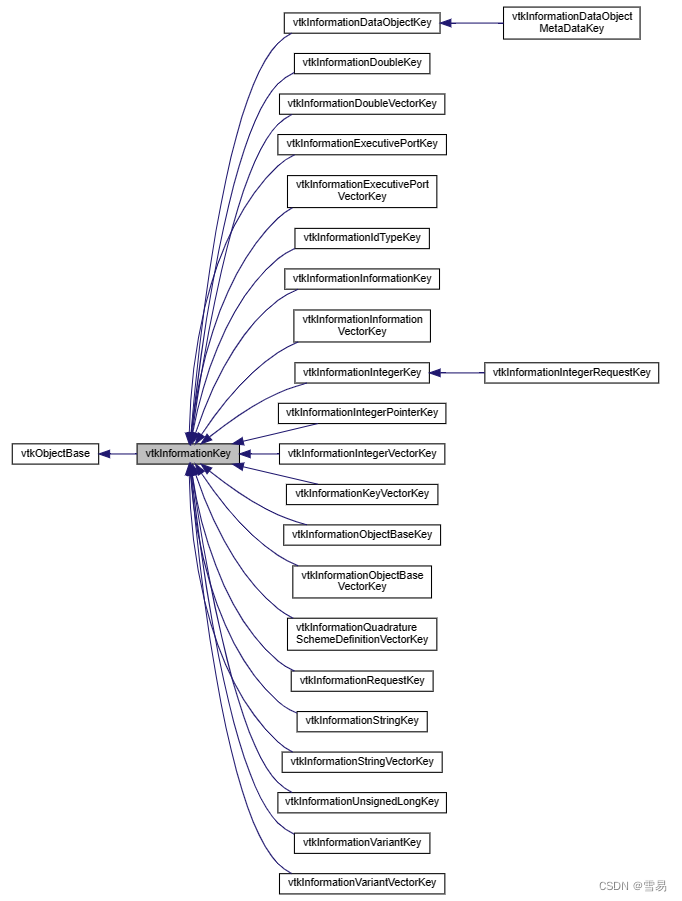
VTK-vtkInformation
前言:本博文主要介绍vtk中的接口vtkInformation的应用,以及vtkInformation的衍生用法,希望对各位小伙伴有所帮助,谢谢!
目录
vtkInformation介绍
描述:
Information中接受的类型: 方法
vtk…
半导体(TSS)放电管的两大选购注意事项及选型小策略
固体放电管,是以半导体工艺制作而成的,因此我们也称为半导体(TSS)放电管,它常在电路中并联使用,具备伏安特性。 TSS放电管在电路中类似开关,在正常工作时不动作,但一般被保护电路受到…
PRE、RC、beta、RTM 含义扫盲
alpha版:内部测试版。α是希腊字母的第一个,表示最早的版本,一般用户不要下载这个版本,这个版本一般是作为技术预览的,很可能包含很多BUG,功能也不全,主要是给开发人员和测试人员测试和找BUG用的。——————————————————————————————————…
直播预告|RTM 助力信令与消息全球实时互通
RTM 是实时消息(Real-time Messaging)的简称。在实时互动场景中,用户通常有两种互动方式:一种是通过音视频进行互动,比如语音连麦、视频连麦等;另一种是通过非音视频的方式进行互动,比如文字聊天…
数据库sql server 2008 r2 RTM版本升级到sql server 2012 r2
(数据库sql server 2008 r2 RTM版本升级到2012)
1.先介绍sql 2008数据库的几个版本
10.00.1600其实就是SQL 2008 10.50.1600其实就是SQL 2008 R2 10.50.2500其实就是SQL 2008 R2 SP1 10.50.4000其实就是SQL Server 2008 R2 SP2 SQL Server 版本号汇总
那么sql server 2008后…
IBM LSF学习(是什么)
碎碎念:这里主要介绍,LSF是什么,本人秉承的写作原则或者技术学习原则,“是什么”,“为什么”,“怎么用”。 这里借鉴了这几篇文章并进行自我理解: https://blog.csdn.net/qq_43653083/article/d…
微软服务器操作系统指什么意思,现代服务器操作系统:你绝对想不到是什么!...
大家好,小编又和大家见面了。上一篇文章,我们了解了Windows Server 2008,今天,我们讲一讲Windows Server 2012。 Windows Server 2012(开发代号:Windows Server 8)是微软的一个服务器系统。这是Windows 8的服务器版本&…
直播选择 RTC 还是 RTMP?
RTC 实时直播
RTC(Real Time Communication)实时音视频通信,它最大的特点就是低延时和无卡顿。从功能流程上说,它包含了采集、编码、前后处理、传输、解码、缓冲、渲染等诸多环节,每一个细分环节,还有更细…
MySQL安装流程 及 8.0与5.7区别
一、MySQL版本介绍
1、MySQL 8.0
窗口函数:MySQL 8.0版本支持窗口函数,这是数据分析工作中非常常用的一类函数。窗口函数可以让用户在单个查询中跨多个行检索数据,并在查询结果中对数据执行计算。隐藏索引:在MySQL 8.0版本中&am…
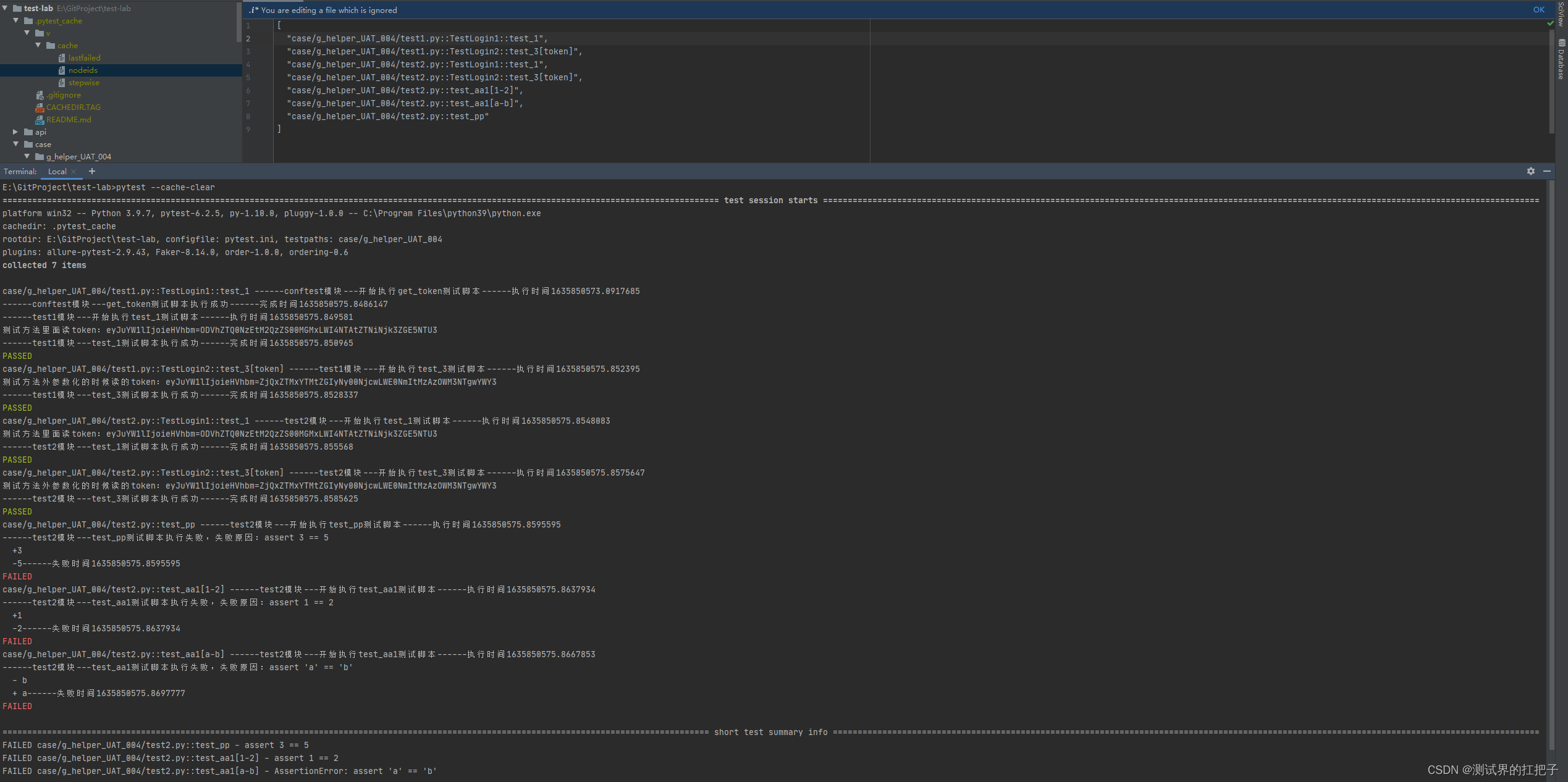
探究Cache缓存功能---【pytest】
前言 pytest运行完用例之后会生成一个 .pytest_cache的缓存文件夹,用于记录用例的ids和上一次失败的用例。 1、跑自动化时经常会出现这样一个情况,一轮自动化跑完后零星出现了几个失败测试用例,无法断定失败的原因,所以可能需要重…
浏览器插件检测淘宝订单是否淘客下单
1、插件安装 。
2、获取接口秘钥 ,获取之后请将接口秘钥填写到本插件中。 3、登录淘宝/天猫已卖出报表列表,点击【检测淘客】按钮,等待返回检测结果;
帝国CMS淘宝客插件,帝国自动调用淘宝客插件链接自动转换
插件功能 可以根据根据设置的字段自动调用淘宝客商品数量,适用于各种资讯和导购站 具体看演示地址,可根据自己的样式来调用数据
淘宝客接入PHP(一)
1、文件位置 extend/tbk文件里面 2、引入tbk的sdk
Loader::import(TopSdk, EXTEND_PATH."/tbk/taobaoke");3、修改autoload文件
直接运行报一下错误,是因为这个类给了namespace的原因。 两种解决方案,1、删除namespace 2、修改为spl_autoloa…
淘宝开放平台Api的小试牛刀(获取淘宝客推广商品信息)
最近在学习淘宝开放平台,属于初学小菜鸟,有一点点小成就给大家分享一下。
要做这个东西,第一步你必须注册为淘宝开发方平台的开发人员。地址:http://open.taobao.com/index.htm
点击加入开放平台,
配图:…
淘宝客高手必备的14大WordPress插件
做淘宝客相信没有人不知道WP的。WordPress一款是用PHP语言和MySQL数据库开发的开源程序。由于WP的安装和使用都非常简单,并且 功能非常强大,可使用的插件和模板数量非常庞大,目前WordPress已经成为国外内主流的Blog搭建平台。WordPress的好处…
java淘宝客开发(一)
java淘宝客开发(一) java淘宝客开发(一)基础 网站建设与权限申请OAuth2权限权限开发测试淘宝客私域用户管理能力调研结果 java淘宝客开发(一)
淘宝客基于CPS模式,带货分佣,这几年短…
电动力学专题:电磁场规范不变性与规范自由度
对称性,不变性,相对性,协变形 在现代物理学中常常被认为具有相同的含义(好拗口)
规范与规范的自由度
保证电磁场物理量不改变的情况下,有多组势可供选择,而每组势可以称为一个规范 规范不变性…
淘宝客工具箱源码,一键转链,淘口令解析 淘宝客中间页生成
淘宝客工具箱,方便淘宝客推广者在微信朋友圈、微信群等渠道进行推广淘口令,生成中间页用于安全推广措施。
因为自己有好几个微信号,都是学生,所以本人做了1年淘宝客,一个月赚个两三千也是钱啊。但是微信做淘客&#x…
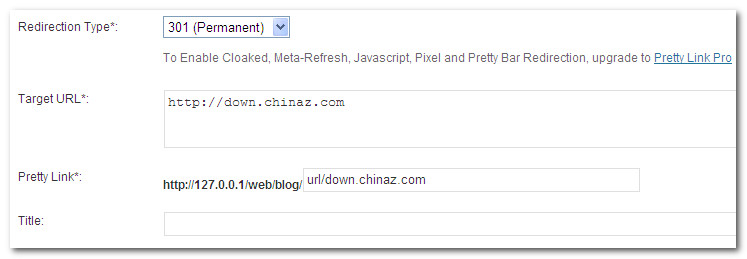
Wordpress淘宝客专用链接跳转插件Pretty Link Lite
很多做淘宝客的朋友在网页优化方面需要一种网址跳转服务,虽然目前有很多网站推出免费的短网址服务,但是也容易导致权重流失,因此多数Wordpress站长肯定更需要这种基于自己域名的短网址跳转插件,可以设置一个简洁的站内链接重定向至…