
层次化可导航小世界(HNSW)图是向量相似性搜索中表现最佳的索引之一。HNSW 技术以其超级快速的搜索速度和出色的召回率,在近似最近邻(ANN)搜索中表现卓越。尽管 HNSW 是近似最近邻搜索中强大且受欢迎的算法,但理解其工作原理并不容易。
本文旨在揭开 HNSW 的神秘面纱,并以易于理解的方式解释这种智能算法。在文章的最后,将探讨如何使用 Faiss 实现 HNSW,并讨论哪些参数设置可以实现所需的性能。
HNSW的基础
我们可以将ANN算法分为三个不同的类别;树、哈希和图。HNSW属于图类别。更具体地说,它是一个基于接近度的图,其中两个顶点根据它们的接近度(更接近的顶点被连接)连接——通常在欧几里得距离中定义。
从“接近度”图到“层次可导航的小世界”图的复杂度有显著的飞跃,将描述两种对HNSW贡献最大的基本技术:概率跳表和可导航的小世界图。
概率跳表
概率跳表由William Pugh在1990年引入,它结合了排序数组的快速搜索能力和链表的便捷插入操作。
跳表通过构建多个层的链表来工作。在最高层,链接能够跳过许多中间节点。在较低层,链接的“跳跃”数量逐渐减少。
要在跳表中进行搜索,从最高层开始,沿着边缘向右移动。如果发现当前节点的“键”大于目标键,表示已经超出目标,于是向下移动到下一层继续搜索。

HNSW继承了相同的分层格式,最高层有更长的边(用于快速搜索)和较低层有更短的边(用于准确搜索)。
可导航的小世界图Navigable Small World Graphs
可导航小世界图(Navigable Small World Graphs,简称NSW)是一种用于向量搜索的高效数据结构,其概念最早在2011至2014年间的学术论文中被提出。这种图经过巧妙地设计,结合了长程和短程链接的特性,使得搜索过程的时间复杂度显著降低。
在NSW图中,每个节点(或称为顶点)都与若干其他节点相连,这些相连的节点被称为“朋友”。每个节点维护着一个朋友列表,共同构成了整个图的结构。
进行NSW图搜索时,搜索过程遵循以下步骤:
- 从预定义的起点出发:选择一个起点,该点与多个相邻节点相连。
- 局部邻近性识别:在这些相邻节点中,识别出与查询向量最为接近的一个节点。
- 逐步逼近目标:移动到该节点,并重复上述过程,逐步缩小搜索范围,直至找到最接近查询向量的节点。
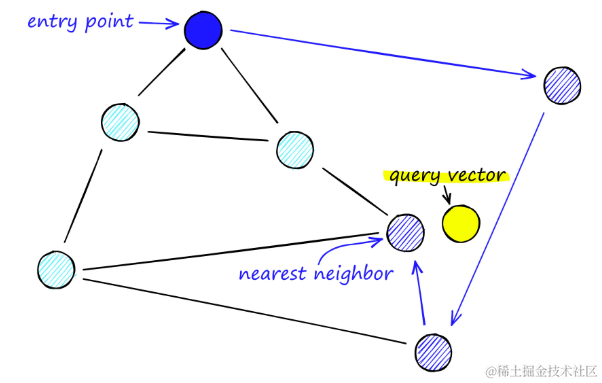
在可导航小世界图(Navigable Small World Graphs,简称NSW)中,搜索过程通过一种称为贪婪路由的方法实现,这种方法通过逐步优化来逼近目标顶点。具体步骤如下:
- 贪婪路由搜索:从任意顶点开始,识别朋友列表中与查询向量最近的相邻顶点,然后转移到该顶点。这个过程重复进行,直到找到一个局部最小值,即当前顶点比之前访问的任何顶点都更接近查询向量,此时停止搜索。
- 局部最小值作为停止条件:当搜索达到一个局部最小值时,认为已经找到了足够接近查询向量的顶点,从而结束搜索过程。
- 网络的可导航性定义:NSW图被定义为能够在多项式或对数时间复杂度内,通过贪婪路由有效搜索的网络结构。
- 贪婪路由的效率问题:在大型网络(顶点数量在1到10K以上)中,如果图的结构不可导航,贪婪路由的效率可能会显著下降。
- 路由的两个阶段:
- 缩小阶段:在搜索初期,优先通过度数较低的顶点进行路由,这有助于快速缩小搜索范围。
- 放大阶段:随着搜索的深入,逐渐转向度数较高的顶点进行路由,这有助于在局部区域内进行更细致的搜索。
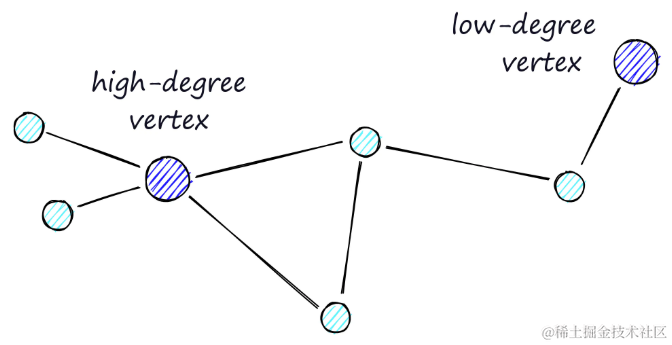
高度顶点有许多链接,而低度顶点链接非常少
搜索过程的有效性依赖于精心设计的停止条件和路由策略,以下是对NSW图搜索策略的优化要点:
- 精确的停止条件:搜索停止的条件是当在当前顶点的“朋友”列表中找不到更接近查询向量的顶点时。这种情况更可能在“缩放”阶段发生,因为在这一阶段,由于顶点的连接数较少,搜索可能过早地结束。
- 避免过早停止:为了减少过早停止的风险并提高搜索的召回率(即确保找到尽可能多的相关顶点),可以考虑增加顶点的平均连接度。然而,这同时会增加网络的复杂性,并可能延长搜索时间。
- 召回率与搜索速度的平衡:在提高召回率和保持搜索速度之间需要找到一个平衡点。这涉及到对顶点的平均度数进行优化,以确保搜索既全面又高效。
- 改进的搜索起点:另一种策略是从连接度较高的顶点开始搜索,即首先进入“放大”阶段。这种方法在处理低维数据时已被证明可以提高NSW图的性能。
创建HNSW
分层导航小世界图(Hierarchical Navigable Small World Graphs,简称HNSW)是可导航小世界图(NSW)的高级演变,它引入了概率跳表结构中的概率多层次概念。
HNSW通过向NSW添加层次化结构,创建一个在不同层级间具有不同链接长度的图。这种结构在最高层拥有最长的链接,在最低层则拥有最短的链接。
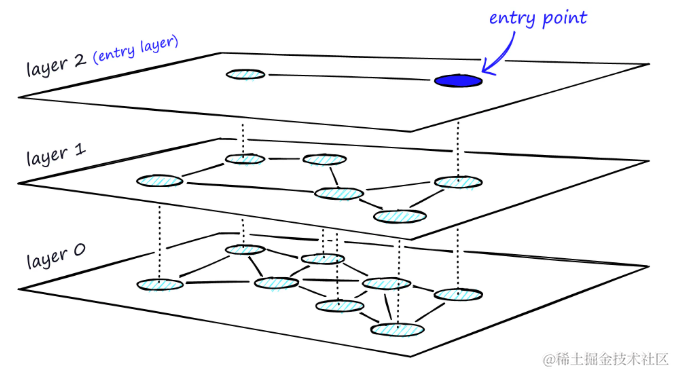
分层图的HNSW,最高层作为入口点,仅包含最长的链接,有助于快速跨越大范围的空间。随着向下层级的移动,链接逐渐变短且数量增多,这有助于在局部区域内进行更精细的搜索
搜索开始于最高层,利用最长的链接快速定位到可能的候选顶点。这些顶点往往是高度顶点,它们跨越多个层具有链接,这为搜索提供了一个自然的“放大”阶段。
通过贪婪路由策略,遍历每一层的链接,逐步向最近的顶点移动,直至达到局部最小值。与NSW不同,在达到局部最小值后,搜索不会停止,而是转移到当前顶点在下一层的对应点,并在那里重新开始搜索。这个过程在每一层重复进行,直到达到最底层(层0)并找到局部最小值为止。
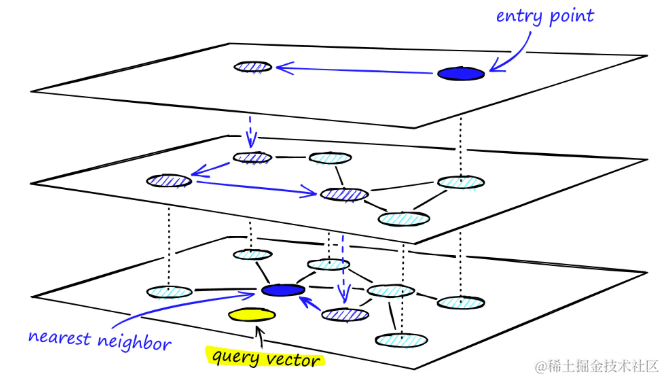
通过 HNSW 图的多层结构的搜索过程
图构建
在图构建过程中,向量是逐个插入的,层数由参数L表示。给定层的向量插入概率由一个概率函数给出,该函数由“层乘数” m L m_L mL规范化,其中 m L = 0 m_L = ~0 mL= 0表示向量仅插入层0。

概率函数对每个层(除了层0)重复,向量被添加到其插入层以及其下的每个层
HNSW的创造者发现,当最小化跨层共享邻居的重叠时,就能获得最佳性能。减少 m L m_L mL可以有助于最小化重叠(将更多向量推到层0),但这会增加搜索过程中的平均遍历次数。因此,使用一个平衡两者的 m L m_L mL值,这个最优值的近似规则是 1 / l n ( M ) 1/ln(M) 1/ln(M)。
图构建从顶部层开始,进入图后,算法贪婪地遍历边,找到插入向量q的ef最近邻居——此时 e f = 1 ef = 1 ef=1。
找到局部最小值后,它移动到下一层,这个过程重复直到达到选择的插入层,这里开始构建的第二阶段。
ef值增加到efConstruction(设置的一个参数),将返回更多的最近邻居。在第二阶段,这些最近邻居是候选链接到新插入元素q以及下一层的入口点。
从这些候选者中选择M个邻居作为链接——最直接的选取标准是选择最接近的向量。
经过多次迭代后,在添加链接时还有两个参数需要考虑。 M m a x M_{max} Mmax定义了顶点可以拥有的最大链接数,以及 M m a x 0 M_{max0} Mmax0定义同样但适用于层0的顶点。
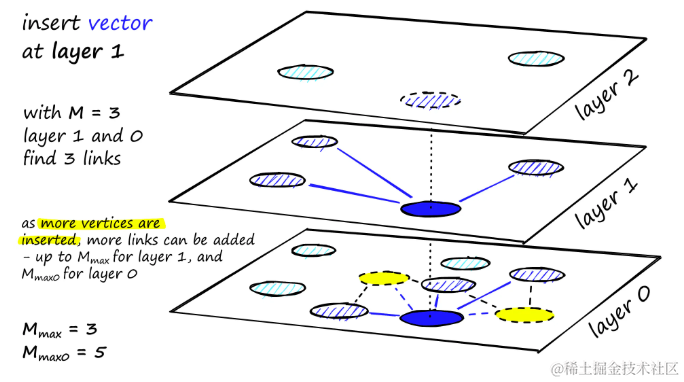
分配给每个顶点的链接数量以及M、 M m a x M_{max} Mmax和 M m a x 0 M_{max0} Mmax0的效果
插入的停止条件是在层0达到局部最小值。
HNSW的实现
使用Facebook AI的相似性搜索库Faiss,可以高效地实现并测试HNSW(分层导航小世界图)的不同构建和搜索参数,进而评估这些参数对索引性能的影响。
初始化HNSW索引
通过以下Python代码初始化HNSW索引:
# 初始化HNSW参数
d = 128 # 向量维度
M = 32 # 每个顶点的邻居数量index = faiss.IndexHNSWFlat(d, M)
print(index.hnsw)
在上述代码中,设置了M参数,它定义了在插入操作中每个顶点将添加的邻居数量。然而,尚未指定M_max和M_max0参数。
在Faiss库中,M_max和M_max0这两个参数在索引初始化时通过set_default_probas方法自动配置。默认情况下,M_max被设置为M的值,而M_max0则设置为M*2
构建索引
在开始使用index.add(xb)添加数据构建索引之前,注意到HNSW索引初始时没有设置层级:
# HNSW索引初始时没有层级
index.hnsw.max_level # -1# 层级(或层次)也是空的
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([], dtype=int64)
一旦添加数据构建索引,max_level和层级信息将自动设置:
index.add(xb)# 添加数据后,层级将自动设置
index.hnsw.max_level # 4# 层级(或层次)现在已填充
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([0, 968746, 30276, 951, 26, 1], dtype=int64)
此时,可以看到图的层级从0到4,正如max_level所描述的那样。levels数组展示每个层上的顶点分布情况。此外,还可以识别出哪个向量是作为图的入口点:
index.hnsw.entry_point # 118295
以上是对Faiss风格的HNSW图的高层次概览。在进行索引性能测试之前,深入了解Faiss如何构建这一结构至关重要。
图结构
在初始化HNSW索引时,指定向量的维度d和每个顶点的邻居数M,这些参数用于调用set_default_probas方法,进而确定每个层级的插入概率。以下是Python中实现这一逻辑的示例:
import numpy as npdef set_default_probas(M: int, m_L: float):nn = 0 # 初始化最近邻居计数为0cum_nneighbor_per_level = []level = 0 # 从层级0开始assign_probas = []while True:# 计算当前层的概率proba = np.exp(-level / m_L) * (1 - np.exp(-1 / m_L))# 当概率低于阈值时,停止创建更多层if proba < 1e-9: breakassign_probas.append(proba)# 除层级0外,每层的邻居数为M;层级0为M*2nn += M*2 if level == 0 else Mcum_nneighbor_per_level.append(nn)level += 1return assign_probas, cum_nneighbor_per_level
此函数构建了两个列表:
assign_probas,表示在特定层级插入的概率cum_nneighbor_per_level,表示在不同层级顶点累积的最近邻居总数
assign_probas, cum_nneighbor_per_level = set_default_probas(32, 1/np.log(32))
assign_probas, cum_nneighbor_per_level
([0.96875,0.030273437499999986,0.0009460449218749991,2.956390380859371e-05,9.23871994018553e-07,2.887099981307982e-08],[64, 96, 128, 160, 192, 224])
输出示例显示了层级0的插入概率远高于其他层级,意味着更高层级更为稀疏,这有助于减少搜索过程中陷入局部最小值的风险,并确保搜索从长距离遍历开始。
接下来,assign_probas向量被用于random_level函数,该函数为每个顶点分配一个插入层级:
def random_level(assign_probas: list, rng):f = rng.uniform() # 从随机数生成器获取随机浮点数for level, proba in enumerate(assign_probas):if f < proba: # 如果随机数小于层级概率return level # 则在此层级插入f -= proba # 否则减去概率值,尝试下一层return len(assign_probas) - 1 # 极低概率下返回最高层级
对于每个层,检查f是否小于assign_probas中为该层分配的概率——如果是,这就是插入层。
如果f太高,从f中减去assign_probas的值,并再次尝试下一个层。这种逻辑的结果是,向量最有可能在层0插入。如果不符合概率条件,将在最高层插入向量,返回len(assign_probas) - 1。如果比较Python实现和Faiss的结果,可以看到非常相似的结果:
chosen_levels = []
rng = np.random.default_rng(12345)
for _ in range(1_000_000):chosen_levels.append(random_level(assign_probas, rng))
np.bincount(chosen_levels) # array([968821, 30170, 985, 23, 1], dtype=int64)
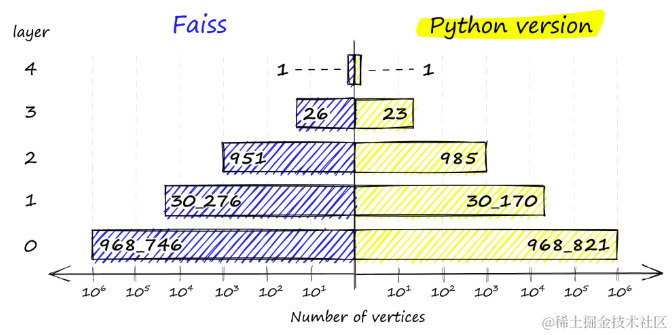
在Faiss实现(左)和Python实现(右)中,顶点在各个层的分布。
Faiss实现确保总是有至少一个顶点在最高层,以作为图的入口点。
HNSW性能
在深入了解了HNSW(分层导航小世界图)的理论基础和Faiss库的实现细节后,现在转向评估不同参数对HNSW索引性能的具体影响。将重点分析召回率、搜索时间、构建时间以及内存使用情况。
将调整以下三个关键参数:M、efSearch和efConstruction,并在Sift1M数据集上测试它们的影响。
-
M 控制每个节点的最大连接数量,影响图的密度和搜索精度。
-
efSearch 控制查询过程中候选列表的大小,影响查询时间和精度。
-
efConstruction 控制索引构建过程中候选列表的大小,影响索引构建时间和质量。
初始化索引:
index = faiss.IndexHNSWFlat(d, M)
设置额外参数:
index.hnsw.efConstruction = efConstruction
index.add(xb) # 构建索引
index.hnsw.efSearch = efSearch
# 执行搜索
index.search(xq[:1000], k=1)
注意,efConstruction必须在构建索引前设置,而efSearch可以在任何时间调整。
召回率与参数的关系
通过调整参数,可以显著影响召回率(recall@1):

各种
M、efConstruction和efSearch参数的recall@1性能
高M和efSearch值对召回率有显著正面影响,而合理的efConstruction值对于优化召回率同样重要。增加efConstruction可以在较低的M和efSearch值下实现更高的召回率。
搜索时间与参数的权衡
尽管提高参数值可以提升召回率,但也显著增加搜索时间:

在搜索1000个查询时,各种
M、efConstruction和efSearch参数的搜索时间(以微秒为单位),y轴使用了对数刻度
搜索时间可以从80%召回率的1毫秒变化到100%召回率的50毫秒,具体取决于参数的选择。如果对召回率的要求不是特别高,搜索时间可以降至0.1毫秒。
对于少量查询,efConstruction对搜索时间的影响不大。但当查询数量增加时,即使是小的efConstruction值变化也可能导致搜索时间的显著增加。
如果查询任务主要是低频的,增加efConstruction参数可以提高召回率,而对搜索时间的影响很小,特别是在使用较低的M值时。
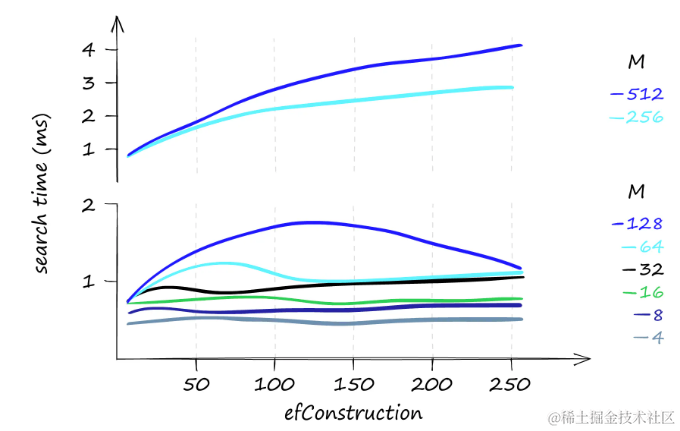
当只搜索一个查询时,
efConstruction和搜索时间。当使用较低的M值时,对于不同的efConstruction值,搜索时间几乎保持不变
内存使用情况
最后,HNSW索引的内存使用情况也是一个重要考量:
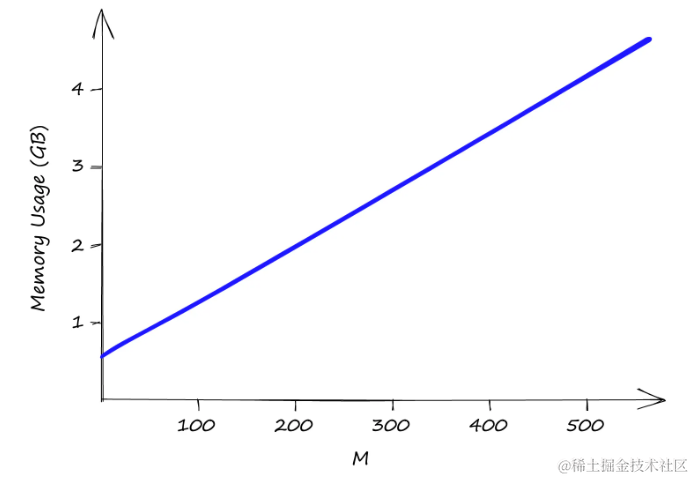
使用Sift1M数据集增加M值时的内存使用情况。
efSearch和fConstruction对内存使用没有影响
efSearch和efConstruction不影响内存使用,而M的值对内存使用有直接影响。即使是较小的M值,索引的大小也可能迅速增加,这可能导致较高的基础设施成本。即使M的值只有2,索引大小已经超过0.5GB,当M为512时,接近5GB。因此,需要权衡高内存使用和由此产生的不可避免的高基础设施成本。
改善内存使用和搜索速度
虽然HNSW索引在内存利用率方面不是最高效的,但如果内存优化是关键需求,可以通过一些策略来改善这一状况。以下是几种提升HNSW性能的方法:
- 使用乘积量化(PQ)压缩:乘积量化(PQ)是一种向量压缩技术,可以在保持相对较高召回率的同时减少内存占用。通过应用PQ,可以在牺牲一定召回率和增加搜索时间的代价下,显著降低内存使用。
- 加速搜索的策略:若目标是提升搜索速度,可以考虑在HNSW索引中集成倒排文件(IVF)组件。IVF通过聚类技术减少搜索空间,从而加快搜索速度。
- 混合使用索引技术:混合使用IVF和PQ等技术可以提供更多的灵活性和性能优化空间。
参考
- HNSW教程
- https://youtu.be/QvKMwLjdK-s
- ANN Benchmarks
- Skip lists: a probabilistic alternative to balanced trees
- Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
- Approximate Nearest Neighbor Search Small World Approach
- Scalable Distributed Algorithm for Approximate Nearest Neighbor Search Problem in High Dimensional General Metric Spaces
- Approximate nearest neighbor algorithm based on navigable small world graphs
- Navigability of complex networks
- Growing homophilic networks are natural navigable small worlds
- Faiss HNSW Implementation



















