文章汇总
动机
相比LoRA,进一步压缩可训练参数以进行微调LFMs。
效果如下:
解决办法
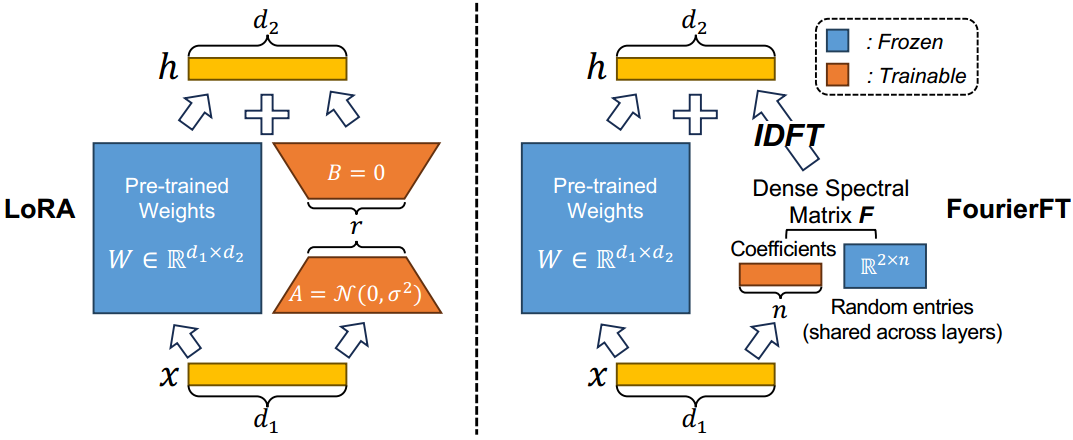
相比LoRA,这里的 Δ W \Delta W ΔW为 E ∈ R 2 × n E\in \mathbb R^{2\times n} E∈R2×n和 c ∈ R n c\in \mathbb R^n c∈Rn。对于所有 L L L个适应层,FourierFT需要存储 n × ( 2 + L ) n\times (2+L) n×(2+L)个参数。需要注意的是,所有层仅训练 c ∈ R n c \in \mathbb R^n c∈Rn向量,同时共享矩阵 E E E( E ∈ R 2 × n E\in \mathbb R^{2\times n} E∈R2×n是冻结的)和超参数 α \alpha α。
具体来说进行如下操作
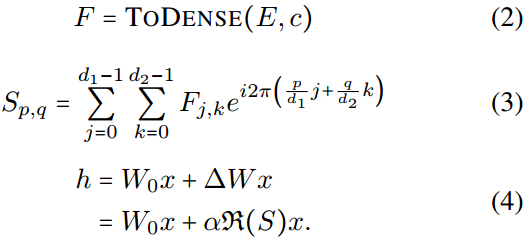
具体来说,Eq. 2中的TODENSE表示构造谱矩阵 F ∈ R d 1 × d 2 F\in R^{d_1\times d_2} F∈Rd1×d2。Eq. 3通过离散傅里叶反变换计算空间矩阵 S S S,其中 i i i表示虚单位。最后,在Eq. 4中,我们取复矩阵 S S S的实部(记为 ℜ ( S ) \Re(S) ℜ(S))并将其乘以 α \alpha α。请注意,所有层都涉及训练各种 c c c向量,同时共享矩阵 E E E和值 α \alpha α。
最后,我们通过对更新后的谱矩阵直接进行离散傅立叶反变换(IDFT)得到权值变化 Δ W \Delta W ΔW。
摘要
近年来,低秩自适应(LoRA)在基础模型的微调方面引起了广泛的关注。通过引入低秩矩阵 A A A和 B B B来表示权重变化,即 Δ W = B A \Delta W=BA ΔW=BA,有效地减少了可训练参数的数量。尽管LoRA取得了进步,但在处理广泛的定制调整或更大的基本模型时,它面临着存储方面的挑战。在这项工作中,我们的目标是利用傅里叶变换的强大表现力进一步压缩可训练参数。具体来说,我们引入傅里叶变换,它将 Δ W \Delta W ΔW作为空间域中的矩阵,并且只学习其光谱系数的一小部分。利用训练好的频谱系数,我们实现离散傅里叶反变换来恢复 Δ W \Delta W ΔW。根据经验,我们的FourierFT方法在各种任务上表现出与LoRA相当或更好的性能,参数更少,包括自然语言理解、自然语言生成、指令调优和图像分类。例如,在LLaMA2-7B模型上执行指令调优时,FourierFT仅以0.064M可训练参数超过LoRA,而LoRA的可训练参数为33.5M。我们的代码发布在https://github.com/Chaos96/fourierft。
1. 介绍
大型基础模型(LFMs)已经在多个领域的任务上展示了卓越的性能,包括自然语言处理(NLP)和计算机视觉(CV)。由于他们令人印象深刻的能力,为广泛的下游任务微调LFMs已经变得普遍(Wang等人,2022;陶瑞等,2023;邱等人,2020)。在全微调范式下,适应每个定制任务的新模型通常包含与原始模型一样多的参数(Qiu et al ., 2020;拉斐尔等人,2020;Chen et al ., 2024;Gao et al ., 2024)。随着模型变大和定制需求的扩展,存储微调检查点的需求也会增加,从而导致昂贵的存储和内存消耗。
LoRA (Hu et al ., 2021)是解决这一问题的一种流行方法,它用两个低秩矩阵 A A A和 B B B表示权重变化,即 W 0 + Δ W = W 0 + B A W_0+\Delta W=W_0+BA W0+ΔW=W0+BA。尽管LoRA具有出色的性能,但其庞大的可训练参数仍然带来了很高的IT基础设施消耗,这对公共社区和个人用户两端都有影响。对于前者,一个直观的例子是,用于特定类型的稳定扩散模型(Rombach et al, 2022)的LoRA适配器(微调权重)需要大约40MB的内存。这就需要LFM社区承担高存储和带宽成本,以满足庞大的用户群。对于后者,更少的参数意味着在移动应用程序中加载微调权重时直接节省RAM,从而为个人用户提供足够的定制(Zhou et al, 2022)。为此,我们自然会问这样一个问题:我们如何进一步压缩可训练参数以进行微调LFMs?
以前的工作已经证明了傅里叶基在数据压缩中的强大表现力,其中极其稀疏的频谱信息可以用来恢复高保真数据(例如,1D信号向量)(Zwartjes & Gisolf, 2007;Duarte & Baraniuk, 2013;Rudelson & Vershynin, 2008)和2D图像矩阵(Vlaardingerbroek & Boer, 2013;Song等,2021;Shi et al ., 2014)。更重要的是,当处理缺乏强空间语义和非频率稀疏的更一般的(非图像)矩阵时,傅里叶变换仍然可以有效地处理恢复(Chen & Chi, 2013;Yang & Xie, 2016)。基于此,我们研究了用其稀疏谱系数更新权重变化 Δ W \Delta W ΔW用于微调LFMs的潜力。
在本文中,我们的目标是积极地减少微调LFMs的可训练参数的数量。为此,我们提出FourierFT (Fourier Transform for Fine-Tuning),它将权重变化 Δ W \Delta W ΔW作为空间域中的矩阵,并学习其稀疏谱系数。具体来说,我们首先随机选择所有层共享的 n n n个谱项。对于每一层,FourierFT学习位于这 n n n个选定条目的 n n n个谱系数,然后直接应用离散傅里叶反变换来计算更新后的 Δ W \Delta W ΔW。因此,微调具有 L t L_t Lt层的预训练模型只需要为fourerft存储 2 n 2n 2n个入口参数和 n L t nL_t nLt系数参数。

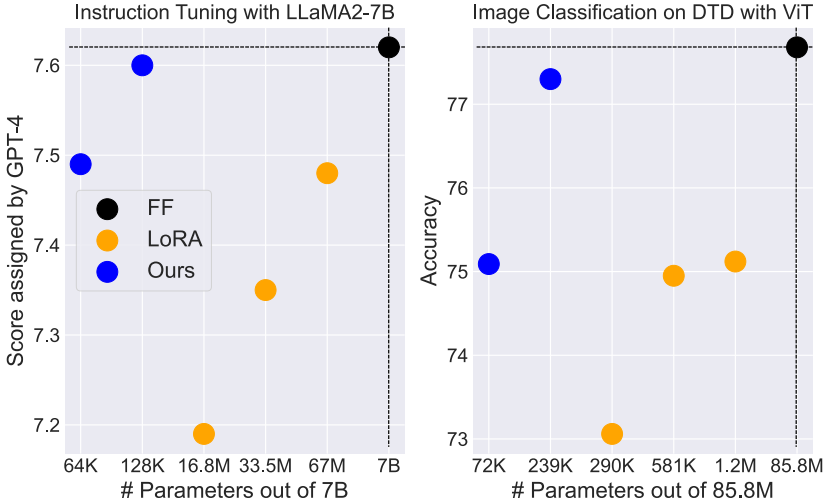
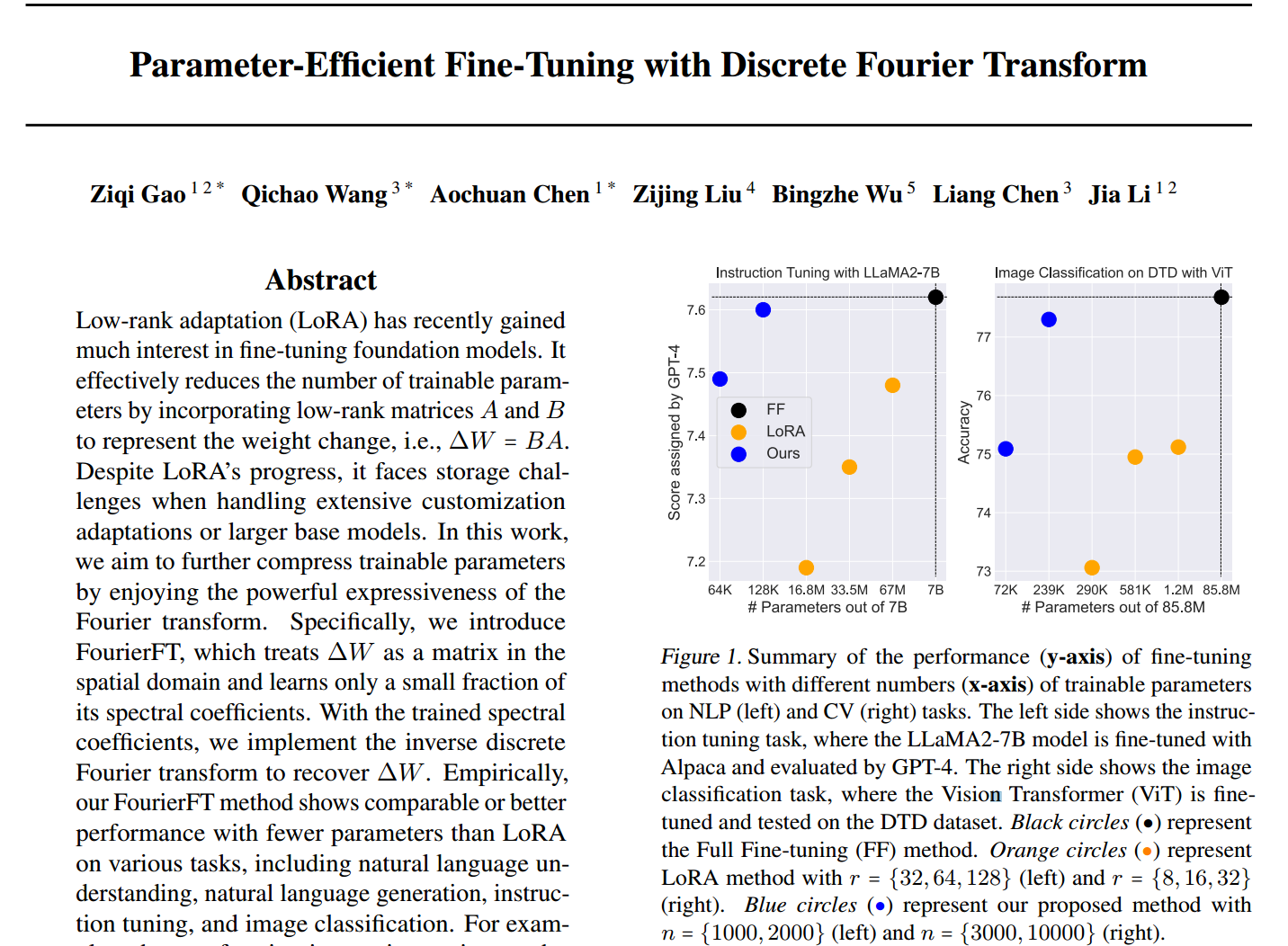
图1所示。在NLP(左)和CV(右)任务上,不同可训练参数数量(x轴)的微调方法的性能(y轴)总结。左侧显示指令调优任务,其中LLaMA2-7B模型使用Alpaca进行微调,并通过GPT-4进行评估。右侧显示图像分类任务,其中对视觉转换器(Vision Transformer, ViT)进行了微调,并在DTD数据集中进行了测试。黑色圆圈(●)表示完全微调(FF)方法。橙色圆圈(●)表示LoRA方法, r = { 32 , 64 , 128 } r =\{32,64,128\} r={32,64,128}(左), r = { 8 , 16 , 32 } r =\{8,16,32\} r={8,16,32}(右)。蓝色圆圈(●)代表我们提出的方法,左边 n = { 1000 , 2000 } n =\{1000,2000\} n={1000,2000},右边 n = { 3000 , 10000 } n =\{3000,10000\} n={3000,10000}。
在经验上,我们将我们的方法与最先进的LoRA变体和其他参数高效的微调方法在各种任务上进行了比较,包括:(1)自然语言理解(在GLUE基准上),(2)自然语言生成(在E2E基准上),(3)指令调优(使用llama家族模型)和(4)图像分类(使用视觉变压器)。FourierFT总能达到与LoRA相当甚至更好的性能,对于这4个任务,其可训练参数分别约为LoRA的6.0%、9.4%、0.2%和9.2%。例如,在图1中,在指令调优任务中,我们的FourierFT方法仅使用64K可训练参数就优于LoRA。此外,它达到了与只有128K参数的完全微调相当的分数。
3. 方法
我们提出傅立叶变换(如图2所示),一种基于离散傅立叶变换的参数高效微调方法。FourierFT遵循LoRA提出的只学习预训练权值变化的原则(Hu et al ., 2021)。然而,与LoRA不同的是,FourierFT不采用低秩结构,而是学习一组傅立叶基的谱系数。具体来说,我们随机初始化光谱条目矩阵,该矩阵被冻结并在所有层之间共享。我们使位于选定条目的谱系数可训练,它们共同构成谱矩阵。最后,我们将离散傅里叶反变换应用于频谱矩阵,在更新权重变化时产生其空间域对应项。

图2。LoRA的概述(左)和我们的FourierFT(右)方法。在LoRA中,只训练低秩( r r r)矩阵 A A A和 B B B。权重变化用它们的乘法表示,即 Δ W = B A \Delta W=BA ΔW=BA。对于每个预训练权值 Δ W = B A \Delta W=BA ΔW=BA, LoRA中可训练参数的理论个数为 r × ( d 1 + d 2 ) r \times (d_1+d_2) r×(d1+d2)。在FourierFT中,我们首先随机生成谱条目矩阵 R 2 × n R^{2\times n} R2×n,该矩阵在所有层之间共享,以减少参数存储需求。完整的谱矩阵由一个可训练系数向量 R n R^n Rn组成, R n R^n Rn位于选定的项上,0位于剩余的项上。我们通过对更新后的谱矩阵直接进行离散傅立叶反变换(IDFT)得到权值变化 Δ W \Delta W ΔW。对于所有 L L L个适应层,FourierFT需要存储 n × ( 2 + L ) n\times (2+L) n×(2+L)个参数。
3.1. Forward Pass
我们遵循仅学习权重变化的范例,这是基于lora的方法所采用的(Hu等,2021;Dettmers等,2023;Zhang et al, 2023)。这可以通过合并预训练的权重及其变化来避免推理延迟。形式上,我们定义每个预训练的权值矩阵为 W 0 ∈ R d 1 × d 2 W_0\in R^{d_1\times d_2} W0∈Rd1×d2,微调的权值变化为 Δ W ∈ R d 1 × d 2 \Delta W\in R^{d_1\times d_2} ΔW∈Rd1×d2。LoRA的目的是将前向通道中的 Δ W \Delta W ΔW以低秩分解的形式参数化:
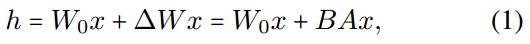
其中,秩 r ≪ min ( d 1 , d 2 ) r\ll \text{min}(d_1,d_2) r≪min(d1,d2)的 B ∈ R d 1 × r B\in R^{d_1\times r} B∈Rd1×r和 A ∈ R r × d 2 A\in R^{r\times d_2} A∈Rr×d2为可训练矩阵。
傅里叶变换的优点是正交和表达的傅里叶基能够恢复信息权重变化。这表明可以用更少的参数实现与LoRA相当的性能。我们首先随机初始化包含离散二维谱项的条目矩阵 E ∈ R 2 × n E\in R^{2\times n} E∈R2×n。然后我们将系数 c ∈ R n c\in R^n c∈Rn随机初始化为正态高斯分布。提出的前向通道是:
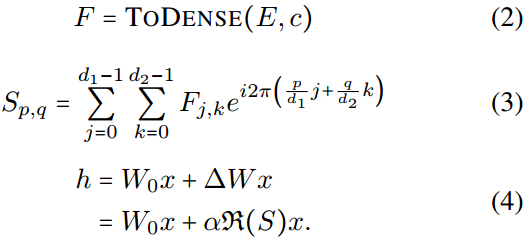
具体来说,Eq. 2中的TODENSE表示构造谱矩阵 F ∈ R d 1 × d 2 F\in R^{d_1\times d_2} F∈Rd1×d2,即 F j , k = c l F_{j,k}=c_l Fj,k=cl (resp. 2)。0),如果 j = E 0 , l & k = E 1 , l j=E_{0,l}\&k=E_{1,l} j=E0,l&k=E1,l(其他的)。Eq. 3通过离散傅里叶反变换计算空间矩阵 S S S,其中 i i i表示虚单位。最后,在Eq. 4中,我们取复矩阵 S S S的实部(记为 ℜ ( S ) \Re(S) ℜ(S))并将其乘以 α \alpha α。请注意,所有层都涉及训练各种 c c c向量,同时共享矩阵 E E E和值 α \alpha α。
FourierFT的伪代码显示为算法1,遵循PyTorch风格。

前人的研究缺乏对谱项在权值变化中的重要性的研究。因此,我们通过引入可调频率偏置来填补这一空白,从而使条目更有可能在该区域进行采样。除了在完整的 d 1 × d 2 d_1\times d_2 d1×d2大小的谱矩阵中随机采样条目(即无偏差)之外,我们还实现了对有利的中心频率(例如,低、中或高频)的偏置条目采样。形式上,我们应用高斯带通滤波器(Gonzales & Wintz, 1987)对 ( u , v ) (u,v) (u,v)项, 0 ≤ u ≤ d 1 − 1 , 0 ≤ v ≤ d 2 − 1 0\le u \le d_1-1,0\le v \le d_2-1 0≤u≤d1−1,0≤v≤d2−1的采样概率进行建模:
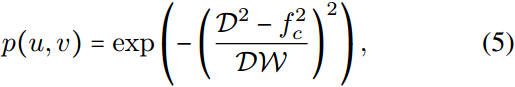
其中, D D D表示点 ( u , v ) (u,v) (u,v)到原点(矩阵中心)的距离, f c f_c fc为首选中心频率, W W W为带宽。在图3中,我们可视化了不同 f c f_c fc和 W = 200 W = 200 W=200的 768 × 768 768\times 768 768×768大小的光谱矩阵的采样概率图。
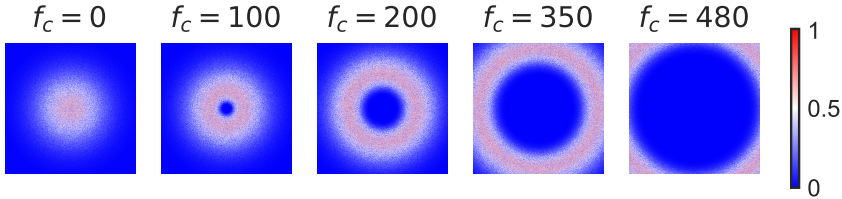
图3。不同有利中心频率 f c f_c fc下入口采样概率的可视化。
请注意,除非特别说明,fourerft默认设置为无频率偏置的条目初始化。
3.2. 参数总结
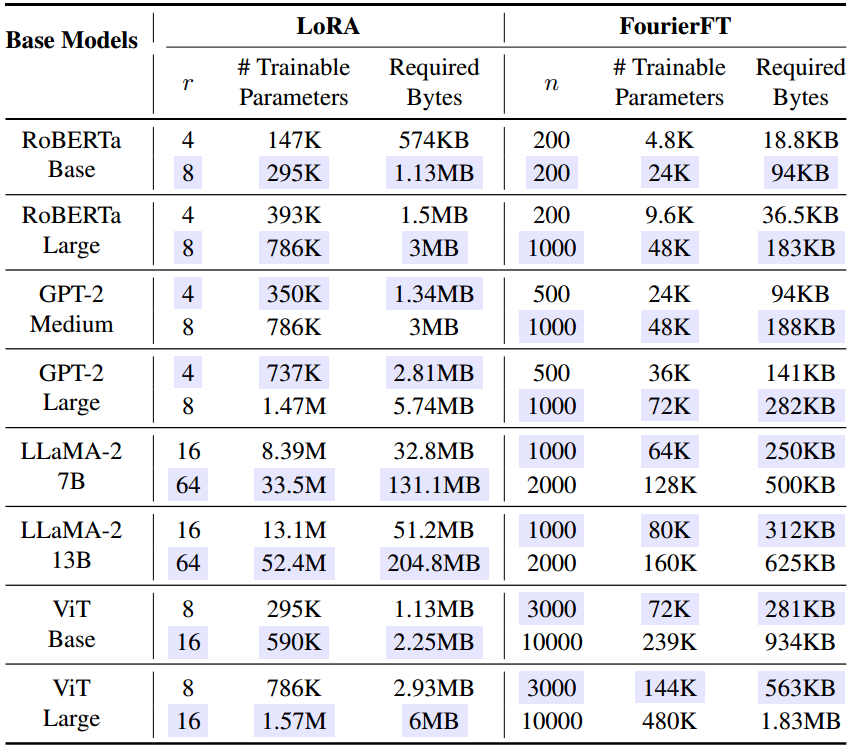
表1。可训练参数的理论数量和微调的存储要求。对于LoRA和FourierFT方法,只有查询层和值层在转换器体系结构中进行调优。在“实验”部分中精确选择的配置将被突出显示。
我们在表1中总结了LoRA和FourierFT可训练参数的数量。LoRA依赖于每一层的一对可训练矩阵 A A A和 B B B。设用于微调的层数为 L t L_t Lt。LoRA中参数的总数由秩 r r r和权重 d = d 1 = d 2 d = d_1 = d_2 d=d1=d2的维数决定: ∣ Θ ∣ L o R A = 2 × d × L t × r {|\Theta|}_{LoRA}=2\times d\times L_t\times r ∣Θ∣LoRA=2×d×Lt×r。对于傅里叶,总数的形式为: ∣ Θ ∣ F o u r i e r F T = n × L t {|\Theta|}_{FourierFT}=n\times L_t ∣Θ∣FourierFT=n×Lt。作为一个直观的例子,RoBERTa Base模型包含12个 d = 768 d = 768 d=768的transformer块,当我们只微调查询和值块时,结果是 L t = 24 L_t = 24 Lt=24层。因此,我们有 ∣ Θ ∣ L o R A = 294 {|\Theta|}_{LoRA}=294 ∣Θ∣LoRA=294,当 r = 8 r = 8 r=8时为 912 912 912,当 n = 1000 n = 1000 n=1000时为 ∣ Θ ∣ F o u r i e r F T = 24 , 000 {|\Theta|}_{FourierFT}=24,000 ∣Θ∣FourierFT=24,000。在表1中,我们强调了在随后的实验中LoRA和我们的方法实现匹配性能的配置。我们注意到,随着模型的尺度(深度和宽度)的增加(例如,RoBERTa Base→RoBERTa Large), FourierFT中参数效率的优势变得更加明显。这可能是因为 ∣ Θ ∣ L o R A {|\Theta|}_{LoRA} ∣Θ∣LoRA与宽度 d d d有明确的线性关系,而不像 ∣ Θ ∣ F o u r i e r F T {|\Theta|}_{FourierFT} ∣Θ∣FourierFT。
4. 实验
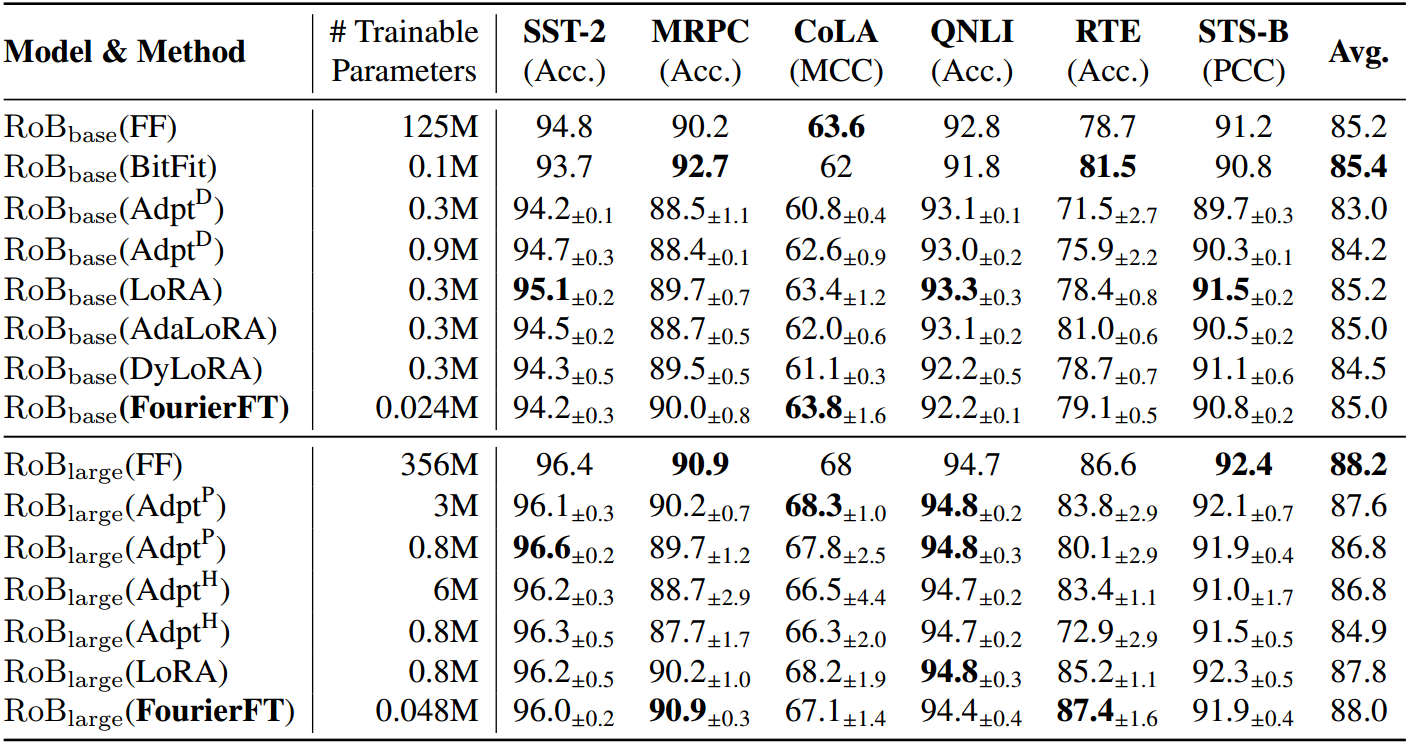
表2。基于RoBERTa Base (RoBbase)和RoBERTa Large (roblage)模型的各种微调方法在GLUE基准测试的6个数据集上的性能。我们报告了CoLA的马修相关系数(MCC), STS-B的皮尔逊相关系数(PCC)和所有其余任务的准确性(Acc.)。我们报告5次运行的中位数结果,每次使用不同的随机种子。每个数据集的最佳结果以粗体显示。6个数据集的所有指标越高越好。
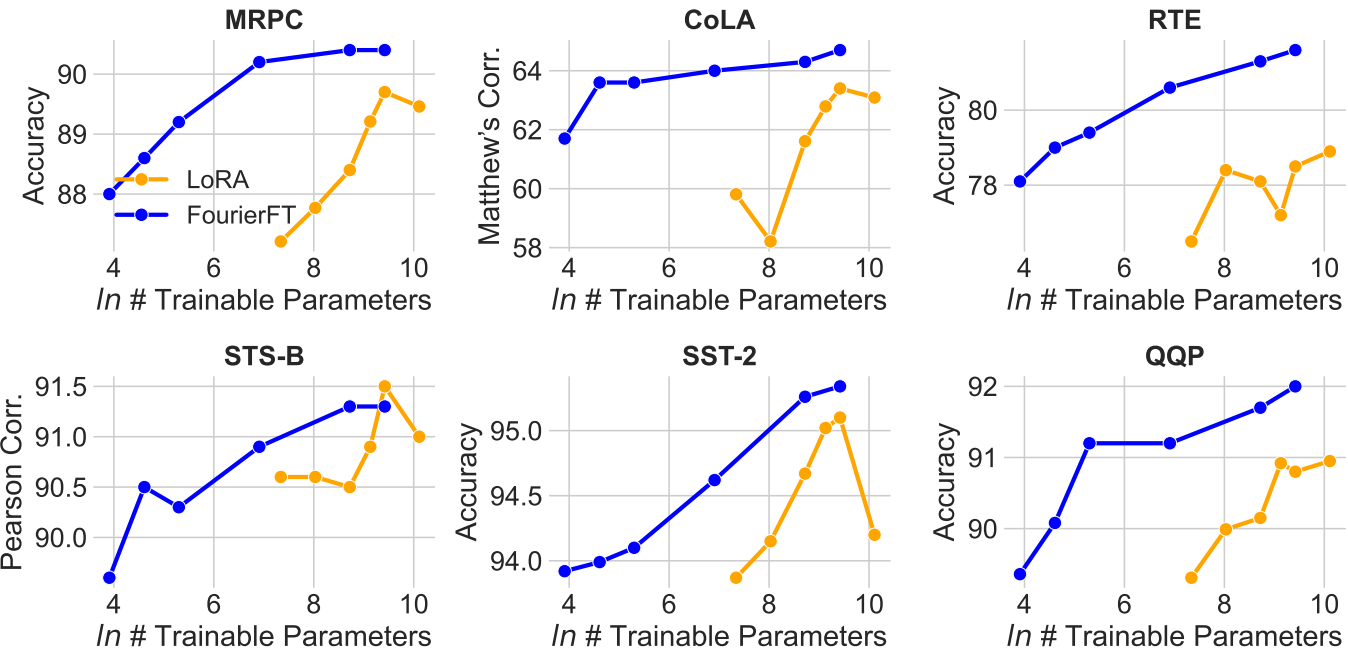
图4。使用RoBERTa Base在GLUE基准测试上的性能对比LoRA和我们的可训练参数(每层)的数量。对于所有6个数据集,我们对LoRA应用r ={1,2,4,6,8,15}的设置,n ={50,100,200,1000,6144,12288}。
5. 结论
在本文中,我们的目标是为大型基础模型的单个微调实现极低的存储内存。这将允许针对不同的域、任务或用户首选项定制多个微调。为了实现这一点,我们提出了一种简单而强大的微调方法,将权重变化视为空间域矩阵和只学习谱域的稀疏系数。与lora风格的基线相比,我们的方法在NLP和CV领域的广泛任务中减少了约8 ~ 500倍的可训练参数数量。
参考资料
论文下载(ICML 2024)
https://arxiv.org/abs/2405.03003
代码地址
https://github.com/Chaos96/fourierft