原文链接：
大模型是这样训练的

AI因你而升温，记得加个星标哦！

大家好，我是泰哥。距离上次写技术贴已经1年有余，这一年当中算法技术的发展可以说是日新月异。今天和大家聊聊大模型的训练的三个阶段，分别为有监督学习（SFT）、奖励模型训练（RW）与强化学习（PPO）阶段，我对以上的训练过程会加上一些自己的理解。

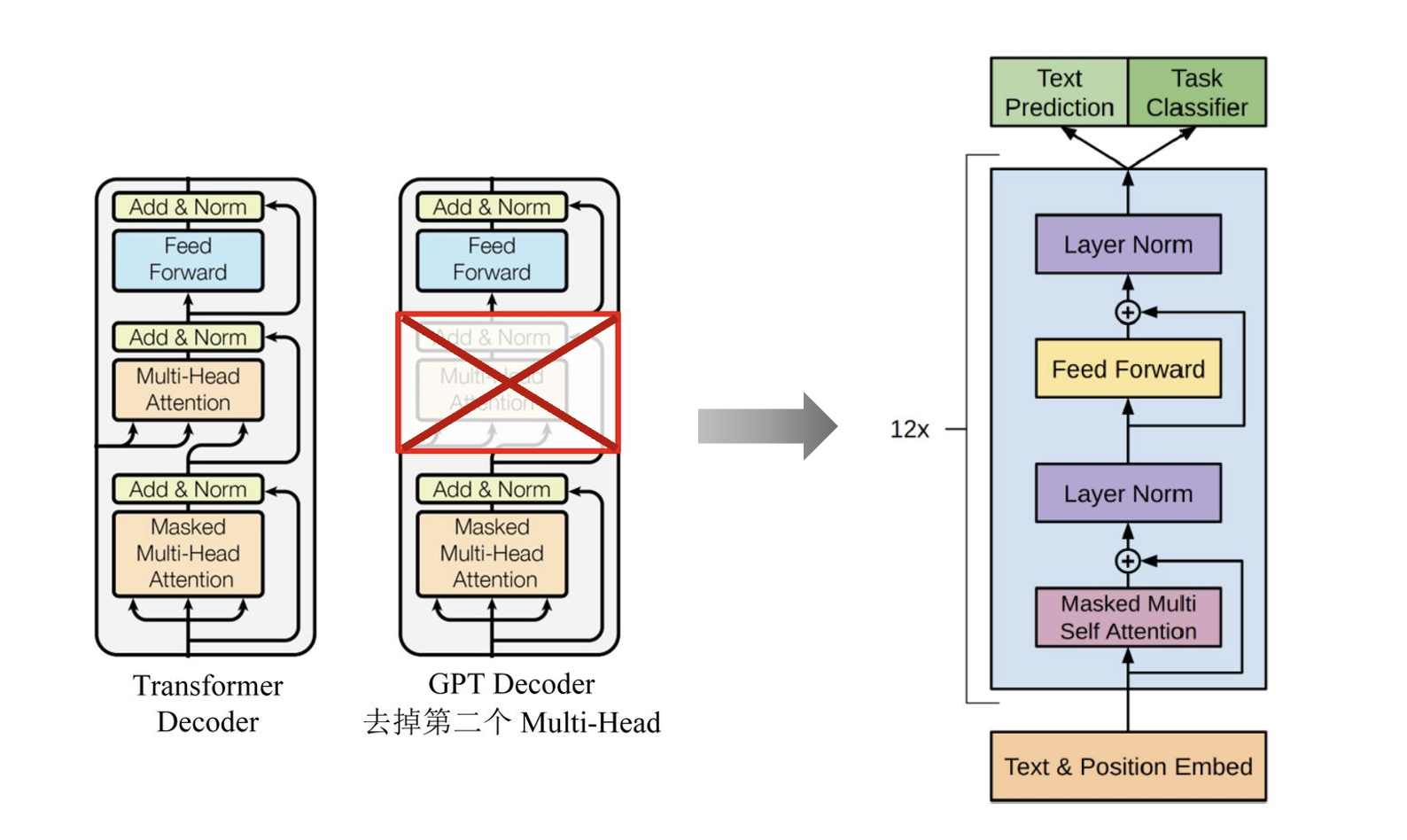
GPT使用Transformer decoder部分作为语言模型的框架，并将decoder中的Multi-head Attention层删除，其结构和计算过程如上图。因为decoder中的第一个自注意力计算中有Mask机制，所以计算每个单词的预测概率时，只考虑一句话中某个词的左侧词汇信息（单向Transformer）对本词进行预测，并不像Bert和ELMo一样有上下文信息，所以Mask的使用使模型看不见未来的信息，得到的模型泛化能力更强。

其中各个研究院对部分细节有所改良，比如：

• 使用了前归一化（Post-Norm），解释是整体上更难出现梯度消失的问题，使得模型的训练更加稳定。
• 采用旋转位置编码（RoPE），与相对位置编码相比RoPE 具有更好的外推性。外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。

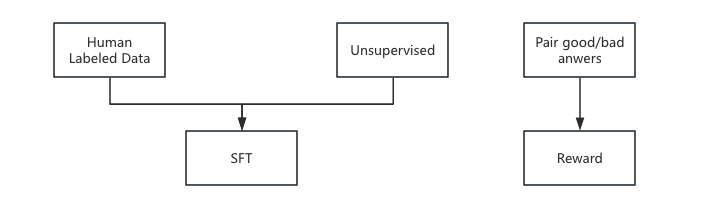
1 有监督学习（SFT）

这个阶段虽然称为有监督学习，但其实在具体实操中，它也是分为了两个步骤：

1. 先使用大量语料进行无监督学习，训练出一个语言模型的基座，这就是大模型的generate方法，展现的是大模型的续写能力
2. 人工整理QA语料对大模型进行有监督训练，这是大模型的chat方法，展现出了大模型的对话能力

2 Reward Model奖励模型训练

大模型会对一个问题回答出的多个不同答案，我们首先需要对这些答案进行优先级标注排序（不是直接打分，因为绝对分数很难统一，我们能更容易的判断出哪个回答更好，使用相对替代绝对），然后根据这个排序结果训练奖励模型。这个模型的底座就是第一阶段训练出的SFT模型，只是把最后一层改为一个神经元即可，就是输出的分数，为一个回归模型，后续将用这个模型对每个回答进行打分评估。

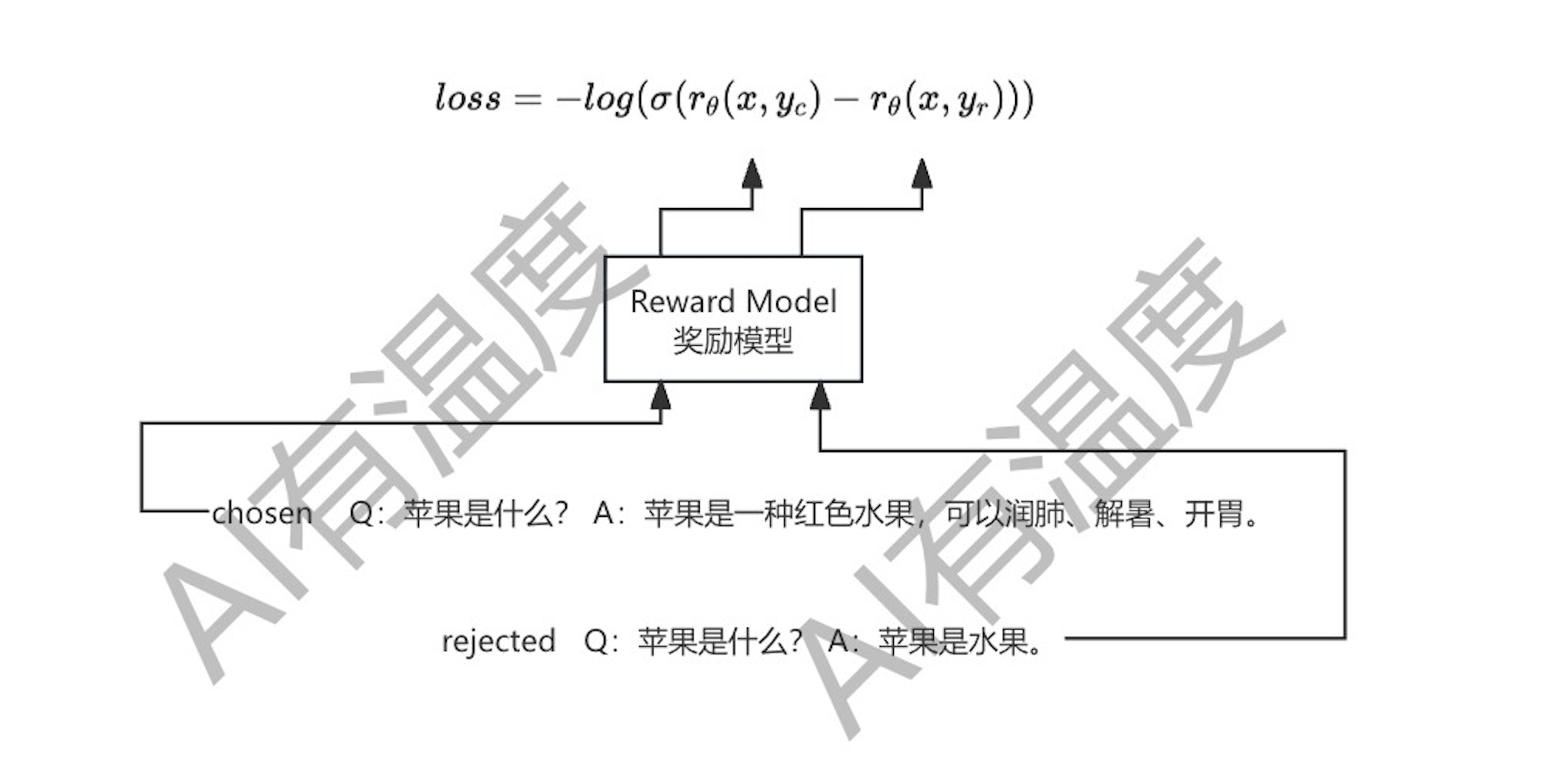
奖励模型的核心是它的损失函数：

$$loss=-log(\sigma (r_{\theta }(x,y_c)-r_{\theta }(x,y_r)))$$

其中c代表chosen，是排名较高的回答，r代表reject，是排名较低的回答。最终的目的就是使排名靠前的回答得分相应的变高。

比如Q：苹果是什么？

A1：苹果是一种红色水果，可以润肺、解暑、开胃。

A2：苹果的品种繁多，根据颜色、大小、口感和用途等不同特点，可以分为多个品种。有的苹果品种适合鲜食，口感脆甜；有的适合烹饪，如做苹果派或苹果酱；还有的适合制酒或制醋。此外，美国苹果公司是全球知名的科技公司。

A3：苹果是水果。

人工标记员打分A2>A1>A3，我们把QA2&QA1、QA2&QA3、QA1&QA3两两放入模型进行打分，然根据损失函数对模型进行反向传播，最后就可以使A2的分数高于A1、A1的分数高于A3。根据不同答案的优先级顺序，就可以训练出奖励模型。

3 强化学习PPO

强化学习的目标就是模型可以自我迭代，其损失函数包括两部分构成：

1. 我们已经进行过有监督训练，所以希望模型的回答结果最好与之前SFT模型的回答分布相近，否则模型可能钻空子，回答一个与有监督答案不符，但是奖励模型给了高分的答案，可以理解为“幻觉问题”。
2. 模型的回答都是高分回答。

我们就是想达到以上要求，所以设计出了如下一系列的训练方法，一共有四个主要模型，分别是：

• Actor Model：演员模型，这就是我们想要训练的目标语言模型
• Critic Model：评论家模型，它的作用是预期收益
• Reward Model：奖励模型，它的作用是计算实际收益
• Reference Model：参考模型，它的作用是给语言模型增加一些“约束”，防止语言模型训歪，使模型的回答结果最好与之前SFT模型的回答分布相近

Actor与Reference的初始化模型就是SFT模型，Reward与Critic的初始化模型就是Reward模型，其中Actor与Critic在后续训练中需要更新参数，而Reward与Reference Model是参数冻结的。

总步骤为下图标注所示，请大家参考：

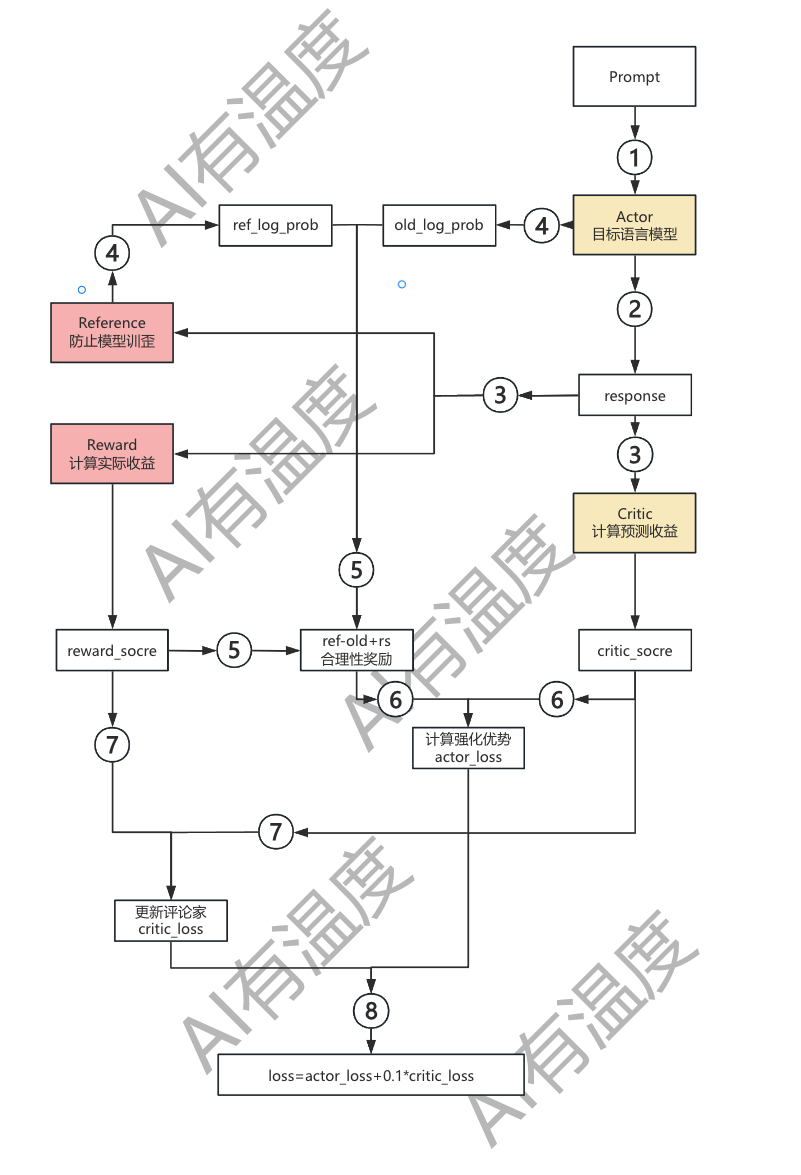
第一步（1号）

给Actor模型输入问题Prompt，Actor模型会有两个输出：

• 生成的回答response
• 还有给出上一部分的文字，每生成下一个字的概率p(token|context)，记为old_log_prob，是一个张量，长度就是response的长度

第二步（3号）

将问题与生成的回答作为输入：

• 输入给Ref模型，会得出在原先模型下输出该句话的张量分布p(token|context)，记为ref_log_prob，是一个张量，长度就是response的长度
• 输入给Reward模型，会得出模型的实际收益，是一个分数
• 输入给Critic模型，评论家会为 response 中的每个 token 计算一个预期收益，第 i个预期收益记为 values[i]

第三步（6号）

首先我们明确强化学习中的一个关键概念——优势。我们将优势定义为“实际获得的收益超出预期的程度”， PPO 计算优势的方法：优势=实际收益-预期收益。预期收益为Critic模型直接计算得出，我们来看看实际收益是如何设计算的。

在第一步与第二步中我们得到了在原先模型下输出的概率分布ref_log_prob与在Actor模型下输出的概率分布old_log_prob。

$$

reward[i]= \begin{cases} ref_log_prob[i] - old_log_prob[i], & \text {i<$N$} \
ref_log_prob[N]-old_log_prob[N]+score, & \text{i=$N$} \end{cases}

$$

来理解一下这个式子（简化的KL散度）：

• ref_log_prob[i] 越高，ref越认可actor的输出，说明输出更守规矩，因此应该获得更高的奖励
• old_log_prob[i] 越高，actor获得的奖励反而更低。old_log_prob[i] 作为正则项，可以保证概率分布的多样性
• 我们只在最后一个token上应用结果正确性奖励（reward_model的输出），加上score分数

通俗来说，整个reward的计算逻辑是典型的霸总逻辑：除非你能拿到好的结果（整句话高分），否则你就得给我守规矩（符合SFT的token分布）。

对于语言模型而言，生成第i个token的实际收益就是：从生成第i个token开始到生成第N个token为止，所能获得的所有奖励的总和。我们用return来表示实际收益，它的计算方式如下：

$$return[i]=reward[i]+...+reward[N]$$

在算出实际收益与预期收益后，要做的就是强化优势动作：

$$a[i]=return[i]-values[i]$$

在语言模型中，根据上下文生成一个 token 就是所谓的“动作”。强化优势动作表示：如果在上下文（context）中生成了某个 token，并且这个动作的优势很高，那么我们应该增加生成该 token 的概率，即增加 p(token|context)的值。

由于演员模型建模了p(token|context)，所以我们可以给演员模型设计一个损失函数，通过优化损失函数来实现“强化优势动作”：

$$actor\_loss=-\frac{1}{N}\sum _{i=1}^{N}a[i]\times p(token[\mathrm{i}]\mid context)$$

其中：

• 当优势大于 0 时，概率越大，loss 越小；因此优化器会通过增大概率（即强化优势动作）来减小 loss
• 当优势小于 0 时，概率越小，loss 越小；因此优化器会通过减小概率（即弱化劣势动作）来减小 loss

$$actor\_loss=-\frac{1}{N}\sum _{i=1}^{N}a[i]\times \frac{p(\text{ token }[\mathrm{i}]\mid \text{ context })}{p_{\text{old }}(\text{ token }[\mathrm{i}]\mid \text{ context })}$$

实际使用时会采用如上公式，$p_{old}$使用的是本次参数更新前的Actor模型。直观来说，当生成某个 token 的概率已经很大了的时候，即便这个动作的优势很大，也不要再使劲增大概率了。或者更通俗地说，就是步子不要迈得太大。

第四步（7号）

前面我们提到过，评论家会为 response 中的每个 token 计算一个预期收益，第 i个预期收益记为 values[i]，因为Critic不准，所以使用损失函数MSE来衡量评论家预期收益和真实收益之间的差距，在提升Actor的同时升级Critic：

$$critic\_loss=\frac{1}{2N}\sum _{i=1}^N(\text{ values }[i]-\mathrm{returns}[i]{)}^2$$

第五部（8号）

最终优化时用的 loss 是演员和评论家损失函数的加权和：

$$Loss=actor\_loss+0.1\times critic\_loss$$

以上就是大模型训练的设计思路及流程。

4 个人理解

大模型在训练过程中损失函数的设计，主要就是为了使模型达到分布合理与分高的双重目的：

1. 在分布合理方面：使用ref_log_prob-old_log_prob进行模拟，同时对大模型正经的胡说八道进行纠正，避免模型回答一个与答案不符但奖励是高分的答案
2. 模型希望答案的分值越高越好

若对模型进行优化，我认为可以加大答案符合原先回答分布概率的权重来进一步优化“幻觉”问题。

5 DPO模型训练方法

RLHF通常包含三个步骤：SFT、 Reward Model、 PPO。该方案优点不需多说，缺点也很明显：训练流程繁琐、算法复杂、超参数多和计算量大，因此RLHF替代方案层出不穷。

DPO（Direct Preference Optimization，直接优化策略）是一种非常高效的RLHF算法。它巧妙地绕过了构建奖励模型和强化学习这两个的繁琐过程，直接通过偏好数据进行微调，效果简单粗暴，在使模型输出更符合人类偏好的同时，极大地缩短了训练时间和难度。

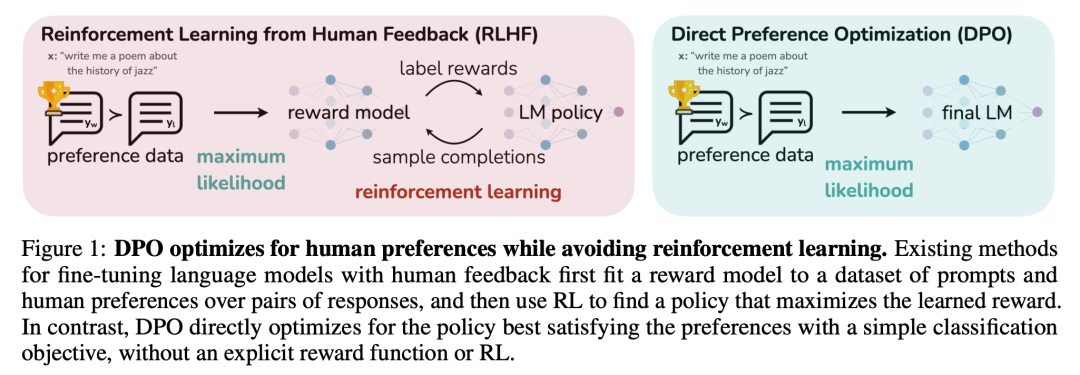
DPO需要的数据与RLHF一致，都是经过人工排序后的QA语料对。主要不同就是损失函数的设计：

$${\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{ref}\right)=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left(y_c\mid x\right)}{{\pi }_{ref}\left(y_c\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_r\mid x\right)}{{\pi }_{ref}\left(y_r\mid x\right)}\right)\right]$$

其中：

• $y_c$是偏好数据对中好的回答 (chosen)，$y_r$则是偏好数据对中坏的回答(rejected)
• ${\pi }_{\theta }\left(y_c\mid x\right)$是当给定输入为x时，当前策略生成好的答案的概率
• ${\pi }_{ref}\left(y_c\mid x\right)$是当给定输入为x时，原始（reference）策略生成好的答案的概率
• 当$-logsigmoid $函数里面的部分越大时，整体的loss就越小，所以对于DPO的loss，我们只需要将$-logsigmoid $函数里面的部分最大化即可。再简化一下上述的loss,只提取$-logsigmoid $函数里面的部分, 我们可以得到：

$$\begin{array}{c}\\ \beta \log \frac{{\pi }_{\theta }\left(y_c\mid x\right)}{{\pi }_{ref}\left(y_c\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_r\mid x\right)}{{\pi }_{ref}\left(y_r\mid x\right)}=\\ \\ \beta \left(\left[\log {\pi }_{\theta }\left(y_c\mid x\right)-\log {\pi }_{\theta }\left(y_r\mid x\right)\right]-\left[\log {\pi }_{ref}\left(y_c\mid x\right)-\log {\pi }_{ref}\left(y_r\mid x\right)\right]\right)\end{array}$$

由此可以看出，其实 DPO 期望最大化的就是奖励模型对chosen数据和rejected数据的差值，从而来达到使模型的回答更偏向于人类排序靠前回答的目标。

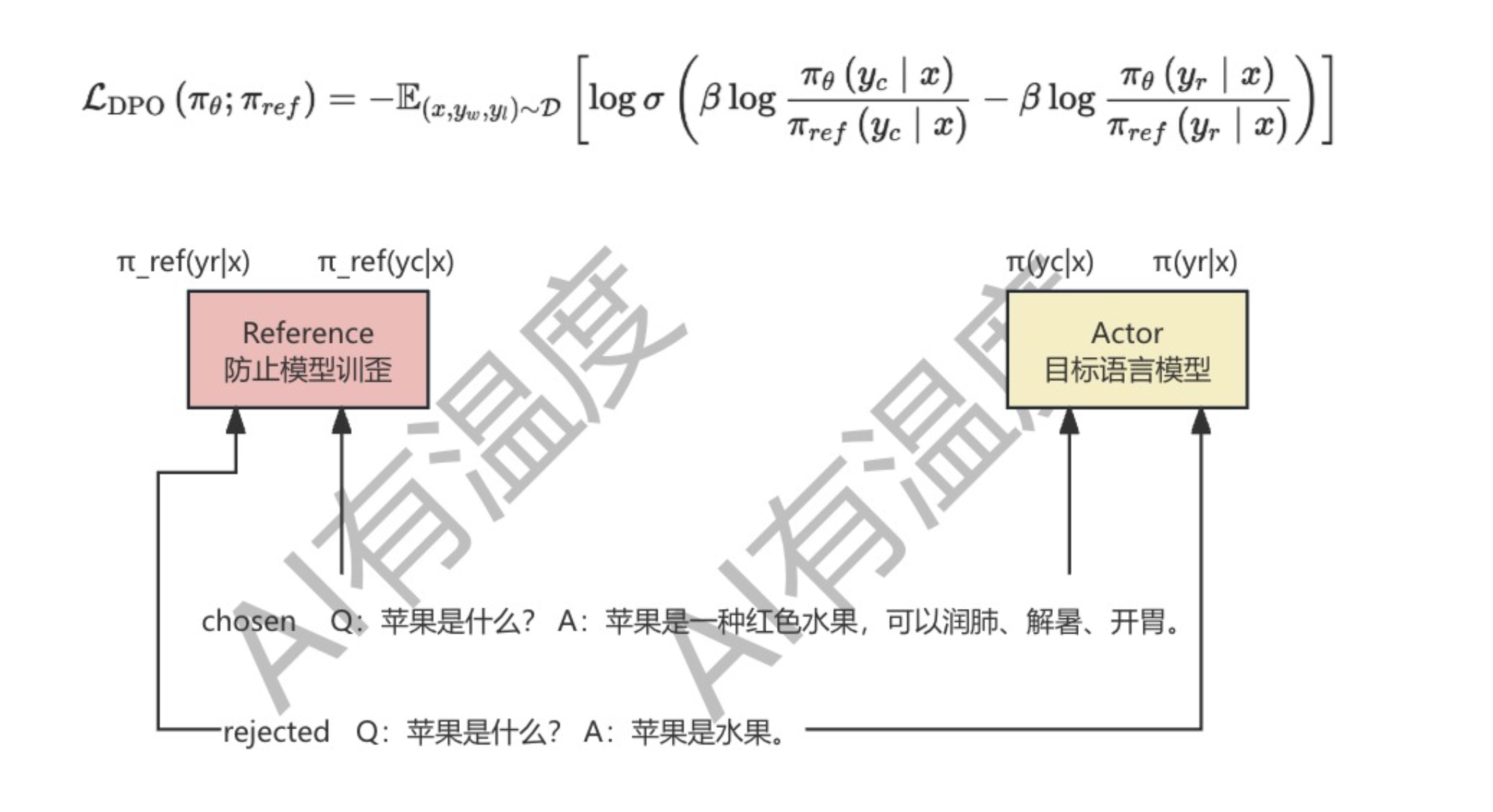
直接策略优化（DPO）算法巧妙地将reward model和强化学习两个步骤合并，使得训练更加的快速高效，在它的训练过程中Reference参数固定，只对目标语言模型进行参数更新，调试更加简单。

在上述DPO推导结果中看似非常完美，但实际使用过程中与PPO优化算法仍有差距，我认为主要是因为DPO的训练目标会导致过拟合, 在下式中的${\pi }_{\theta }\left(y_r\mid x\right)$优化策略为零，那么就可以使得偏好概率变的很大，整体的损失很小。

$${\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{ref}\right)=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left(y_c\mid x\right)}{{\pi }_{ref}\left(y_c\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_r\mid x\right)}{{\pi }_{ref}\left(y_r\mid x\right)}\right)\right]$$

令${\pi }_{\theta }\left(y_r\mid x\right)\to 0$，那么$-\beta \log \frac{{\pi }_{\theta }\left(y_r\mid x\right)}{{\pi }_{ref}\left(y_r\mid x\right)}\to +\infty$，损失就能一下降低下来， 直觉的理解是模型随便胡说的情况下就能使得Loss降低，给了钻空子的空间，没有像PPO损失函数考虑了结果整体的分值，因为PPO的要求是如果除非你能拿到好的结果（整句话高分），否则你就得给我守规矩（结果合理分布）。

原文链接：
大模型是这样训练的