求函数最小值-torch版

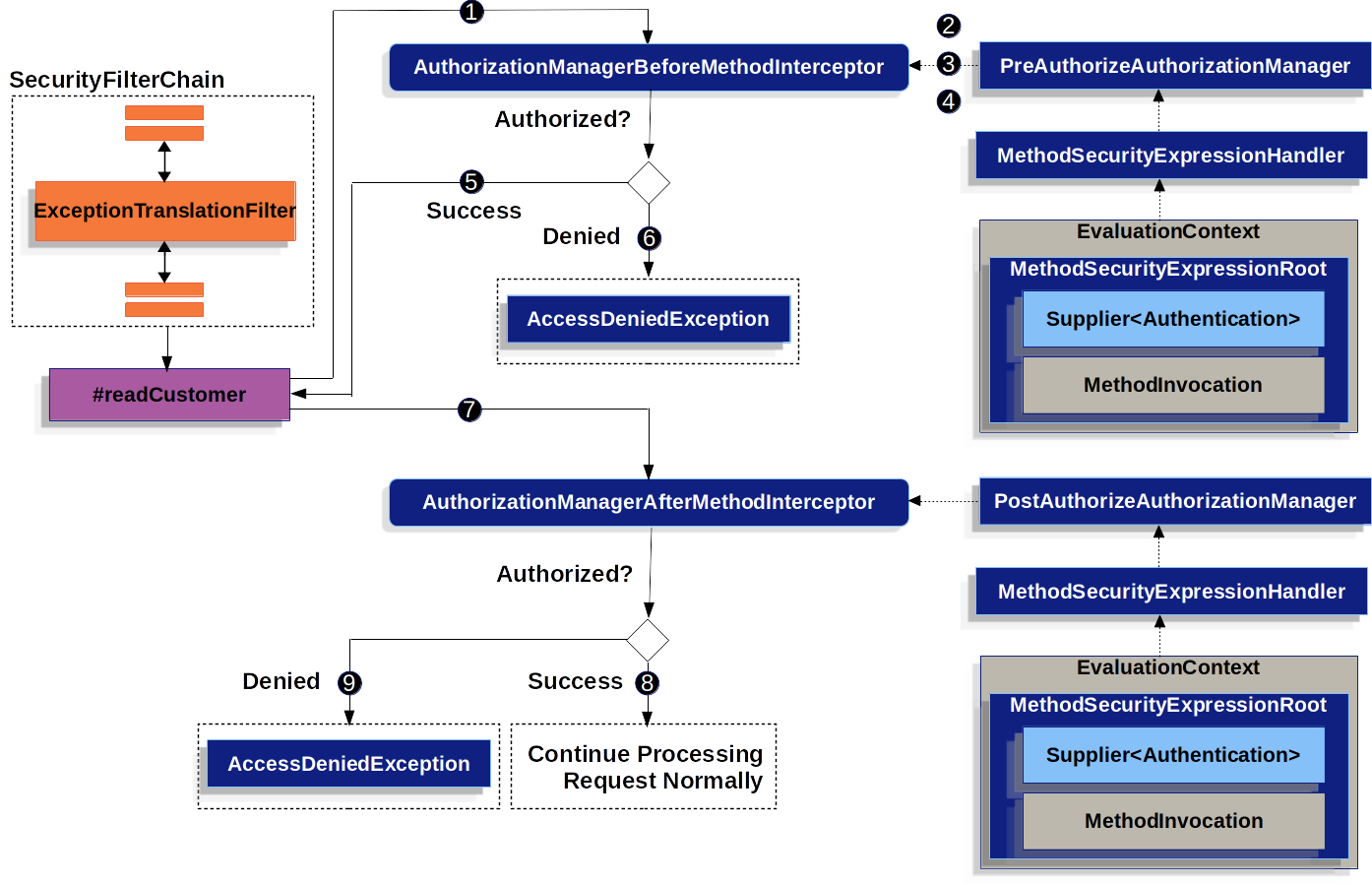
目标：torch实现下面链接中的梯度下降法

先计算 $y=x^2$ 的导函数 $y{}'=2x$ ，然后计算导函数在 $x_{0}=7.5$ 处的梯度 (导数)

让 $x_{0}$ 沿着 梯度的负方向移动，

$x\leftarrow x-y{}'x_{0}$

自变量 $x$ 的更新过程如下

$x_{1}\leftarrow x_{0}-y{}'_{x0}$

$x_{2}\leftarrow x_{1}-y{}'_{x1}$

$x_{3}\leftarrow x_{2}-y{}'_{x2}$

$\cdot \cdot \cdot$

$x_{n}\leftarrow x_{n-1}-y{}'_{x_{n-1}}$

torch代码实现如下

import torchx = torch.tensor([7.5],requires_grad=True)
# print(x.grad)optimizer = torch.optim.SGD([x], lr=1)print('x_0 = {}'.format(x))for i in range(10):y = x * xoptimizer.zero_grad()y.backward()optimizer.step()print('x_{} = {}'.format(i+1,x))

运行效果如下：

x_0 = tensor([7.5000], requires_grad=True)
x_1 = tensor([-7.5000], requires_grad=True)
x_2 = tensor([7.5000], requires_grad=True)
x_3 = tensor([-7.5000], requires_grad=True)
x_4 = tensor([7.5000], requires_grad=True)
x_5 = tensor([-7.5000], requires_grad=True)
x_6 = tensor([7.5000], requires_grad=True)
x_7 = tensor([-7.5000], requires_grad=True)
x_8 = tensor([7.5000], requires_grad=True)
x_9 = tensor([-7.5000], requires_grad=True)
x_10 = tensor([7.5000], requires_grad=True)

给梯度加系数

我们可以给梯度加个系数，如下

$x_{1}\leftarrow x_{0}-0.01*y{}'_{x0}$

$x_{2}\leftarrow x_{1}-0.01*y{}'_{x1}$

$x_{3}\leftarrow x_{2}-0.01*y{}'_{x2}$

$\cdot \cdot \cdot$

$x_{n}\leftarrow x_{n-1}-0.01*y{}'_{x_{n-1}}$

torch代码实现如下

import torchx = torch.tensor([7.5],requires_grad=True)
# print(x.grad)optimizer = torch.optim.SGD([x], lr=0.01)print('x_0 = {}'.format(x))for i in range(10):y = x * xoptimizer.zero_grad()y.backward()optimizer.step()print('x_{} = {}'.format(i+1,x))

运行效果如下：

x_0 = tensor([7.5000], requires_grad=True)
x_1 = tensor([7.3500], requires_grad=True)
x_2 = tensor([7.2030], requires_grad=True)
x_3 = tensor([7.0589], requires_grad=True)
x_4 = tensor([6.9178], requires_grad=True)
x_5 = tensor([6.7794], requires_grad=True)
x_6 = tensor([6.6438], requires_grad=True)
x_7 = tensor([6.5109], requires_grad=True)
x_8 = tensor([6.3807], requires_grad=True)
x_9 = tensor([6.2531], requires_grad=True)
x_10 = tensor([6.1280], requires_grad=True)

调迭代次数

发现 $x$ 变化的很慢，我们可以增加迭代次数，如下

import torchx = torch.tensor([7.5],requires_grad=True)
# print(x.grad)optimizer = torch.optim.SGD([x], lr=0.01)print('x_0 = {}'.format(x))for i in range(200):y = x * xoptimizer.zero_grad()y.backward()optimizer.step()print('x_{} = {}'.format(i+1,x))

运行结果如下：

x_0 = tensor([7.5000], requires_grad=True)
x_1 = tensor([7.3500], requires_grad=True)
x_2 = tensor([7.2030], requires_grad=True)
...
x_199 = tensor([0.1346], requires_grad=True)
x_200 = tensor([0.1319], requires_grad=True)

调梯度系数

我们把 0.01 换成 0.1 试试

import torchx = torch.tensor([7.5],requires_grad=True)
# print(x.grad)optimizer = torch.optim.SGD([x], lr=0.1)print('x_0 = {}'.format(x))for i in range(10):y = x * xoptimizer.zero_grad()y.backward()optimizer.step()print('x_{} = {}'.format(i+1,x))

运行结果如下：

x_0 = tensor([7.5000], requires_grad=True)
x_1 = tensor([6.], requires_grad=True)
x_2 = tensor([4.8000], requires_grad=True)
x_3 = tensor([3.8400], requires_grad=True)
x_4 = tensor([3.0720], requires_grad=True)
x_5 = tensor([2.4576], requires_grad=True)
x_6 = tensor([1.9661], requires_grad=True)
x_7 = tensor([1.5729], requires_grad=True)
x_8 = tensor([1.2583], requires_grad=True)
x_9 = tensor([1.0066], requires_grad=True)
x_10 = tensor([0.8053], requires_grad=True)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://xiahunao.cn/news/3226683.html

如若内容造成侵权/违法违规/事实不符，请联系瞎胡闹网进行投诉反馈，一经查实，立即删除！