文章目录
- 1. 写出Multi-Head Attention
- 2. Pre-Norm vs Post-Norm
- 3. Layer Norm
- RMS Norm
- Batch Norm
- 4. SwiGLU
- 从ReLU到Swish
- SwiGLU
- 5. AdamW
- 6. 位置编码
- Transformer位置编码
- RoPE
- ALibi
- 7. LoRA
- 初始化
- 参考文献
1. 写出Multi-Head Attention
import torch
import torch.nn as nn
import torch.nn.functional as F
import mathclass MHA(nn.Module):def __init__(self, d_model, nums_head):super(MHA, self).__init__() # !!self.d_model = d_modelself.nums_head = nums_headself.wq = nn.Linear(d_model, d_model)self.wk = nn.Linear(d_model, d_model)self.wv = nn.Linear(d_model, d_model)self.dk = d_model/nums_headself.wo = nn.Linear(d_model,d_model)def split_head(self, x, batch_size): # x(batch_size, seq_len, d_model) -> x(batch_size, seq_len, nums_head, d_k) -> x(batch_size, nums_head, seq_len, dk)return x.view(batch_size, self.nums_head, -1, self.dk).transpose(1,2)def forward(self, q, k, v, mask=None):batch_size = q.size(0)q = self.wq(q)k = self.wk(k)v = self.wv(v)q = self.split_head(q, batch_size)k = self.split_head(k, batch_size)v = self.split_head(v, batch_size)scores = torch.matmul(q, k.transpose(-2,-1))/math.sqrt(self.dk)if mask is not None:scores = scores.mask_fill(mask, float('-inf')) # mask_fillweights = F.softmax(scores, dim=-1)attention = torch.matmul(weights, v)concat = attention.transpose(1,2).contiguous().view(batch_size, -1, self.d_model) # contiguousoutput = self.wo(concat)return output
2. Pre-Norm vs Post-Norm
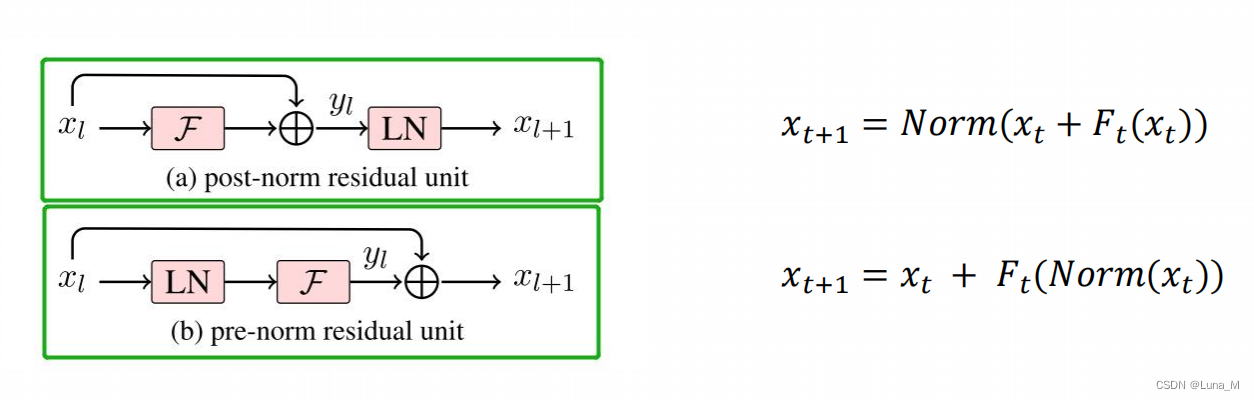
-
Pre-Norm优势:

-
为什么层数较深时,Pre-Norm不如Post-Norm:

3. Layer Norm
任何norm的意义都是为了让使用norm的网络的输入的数据分布变得更好,也就是转换为标准正态分布,数值进入敏感度区间,以减缓梯度消失,从而更容易训练。

这里结合PyTorch的nn.LayerNorm算子来看比较明白:
nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)
- normalized_shape:归一化的维度,int(最后一维)list(list里面的维度),还是以(2,2,4)为例,如果输入是int,则必须是4,如果是list,则可以是[4], [2,4], [2,2,4],即最后一维,倒数两维,和所有维度
- eps:加在分母方差上的偏置项,防止分母为0
- elementwise_affine:是否使用可学习的参数 γ \gamma γ和 β \beta β ,前者开始为1,后者为0,设置该变量为True,则二者均可学习随着训练过程而变化
RMS Norm
与layerNorm相比,RMS Norm的主要区别在于去掉了减去均值的部分
在RMS Norm的论文中指出:RMS Norm 比Layer Norm更快(可以在各个模型上减少约 7%∼ 64% 的计算时间),效果也基本一致。
Batch Norm

- Batch Norm:把每个Batch中,每句话的相同位置的字向量看成一组做归一化。
- Layer Norm:在每一个句子中进行归一化。
- Instance Norm:每一个字的字向量的看成一组做归一化。
- Group Norm:把每句话的每几个字的字向量看成一组做归一化。计算成本较高
4. SwiGLU
- Sigmoid

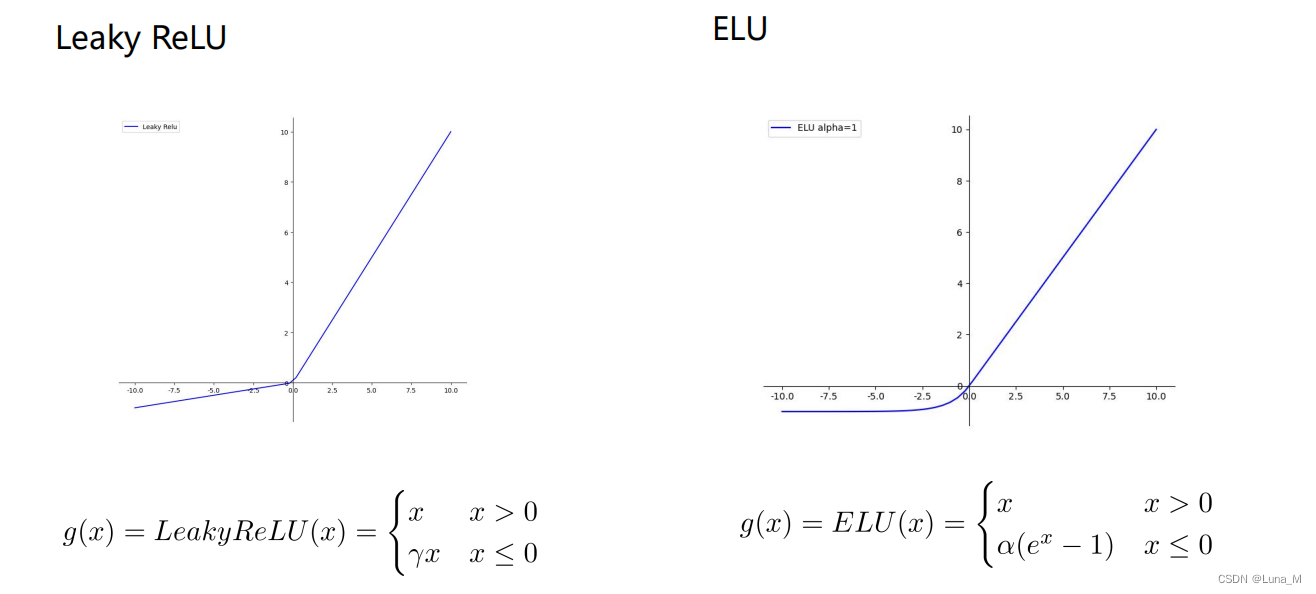
从ReLU到Swish
-
ReLU

-
Leaky ReLU,ELU
-
Swish

-
GELU vs Swish
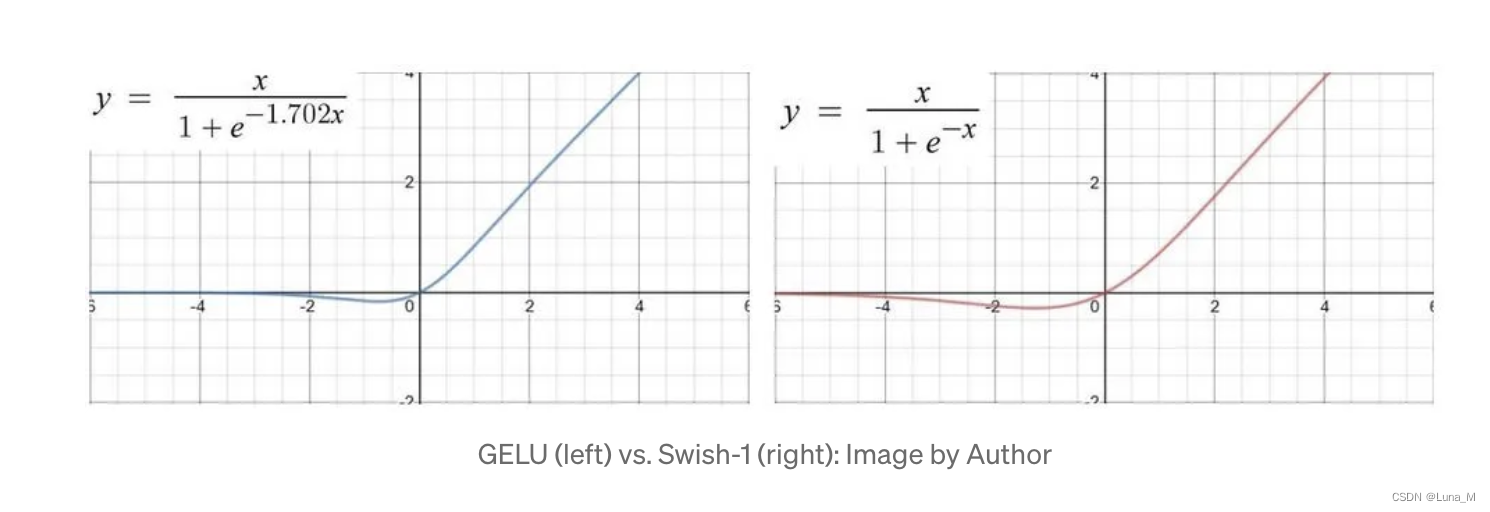
GELU (高斯误差线性单元)与 Swish 激活函数(x · σ(βx))的函数形式和性质非常相像,一个是固定系数 1.702,另一个是可变系数 β(可以是可训练的参数,也可以是通过搜索来确定的常数),两者的实际应用表现也相差不大。
【GPT2, BERT, ALBERT, RoBERTA常用GELU】
SwiGLU
-
GLU
 理解GLU激活函数的关键在于它的门控机制。门控机制使得GLU能够选择性地过滤输入向量的某些部分,并根据输入的上下文来调整输出。门控部分的作用是将输入进行二分类,决定哪些部分应该被保留,哪些部分应该被抑制。
理解GLU激活函数的关键在于它的门控机制。门控机制使得GLU能够选择性地过滤输入向量的某些部分,并根据输入的上下文来调整输出。门控部分的作用是将输入进行二分类,决定哪些部分应该被保留,哪些部分应该被抑制。 -
SwiGLU
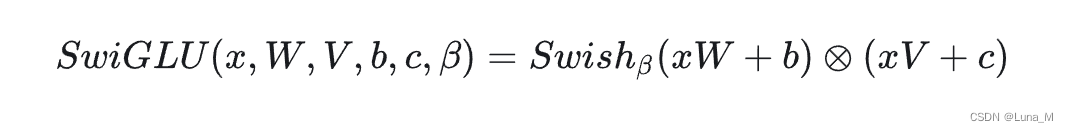
5. AdamW
- Adam
优点:惯性保持 + 自适应

g t \ g_t gt为梯度
 自适应:经常被更新的权重,更新的幅度小一些;不经常被更新的权重,更新的幅度大一些
自适应:经常被更新的权重,更新的幅度小一些;不经常被更新的权重,更新的幅度大一些
- AdamW
Adam的基础上,权重更新时,加入L2正则化项。
之前各类框架对 Adam 的实现中,在损失函数中加入了 L2 正则化项,也就是把权重衰减放到了梯度里,由梯度间接缩小θ。但是这种方法并没有起到有效的正则化作用。AdamW 直接将权重衰减项放到权重计算中,可以对大的权重进行惩罚,起到了有效的正则化作用。
(下图中x表示权重)

6. 位置编码
原因:为 Attention 添加位置信息
没有位置编码的Attention并不能捕捉序列的顺序。(交换单词位置后 Attention map 的对应位置数值也会进行交换,然而并不会产生数值变化)
Transformer位置编码
用sin和cos交替来表示位置,并把位置编码加在embeding上。
RoPE
参考文献
Transformer中sinusoidal位置编码对相对位置关系的表示还是比较间接的,那有没有办法更直接的表示相对位置关系呢?旋转位置编码(Rotary Position Embedding,RoPE)是一种用绝对位置编码来表征相对位置编码的方法,并被用在了很多大语言模型的设计中。
假设通过下述运算来给 q, k 添加绝对位置信息:
f ( q , m ) \ f(q,m) f(q,m) 表示给向量 q q q在位置 m m m添加位置信息, f ( k , n ) \ f(k,n) f(k,n) 表示给向量 k k k在位置 n n n添加位置信息。
同时,我们希望经过 Attention 的内积运算后,内积结果带有相对位置信息:
 RoPE这一研究就是为上面这个等式找到了一组解答,也就是:
RoPE这一研究就是为上面这个等式找到了一组解答,也就是:
f ( q , m ) = q e i m θ \ f(q,m) = qe^{imθ} f(q,m)=qeimθ
根据复数乘法的⼏何意义,该变换实际上对应着向量的旋转,所以我们称之为“旋转式位置编码”,
它还可以写成矩阵形式(二维):
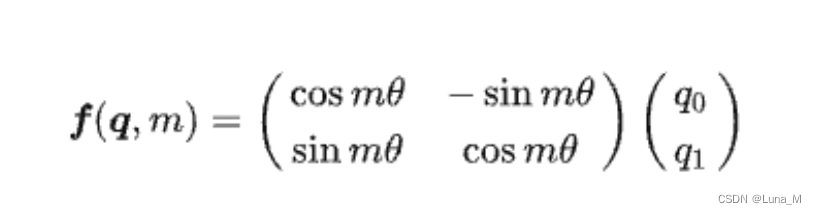 根据刚才的结论,结合内积的线性叠加性,可以将结论推广到高维的情形。可以理解为,每两个维度一组,进行了上述的“旋转”操作,然后再拼接在一起:
根据刚才的结论,结合内积的线性叠加性,可以将结论推广到高维的情形。可以理解为,每两个维度一组,进行了上述的“旋转”操作,然后再拼接在一起:
 由于矩阵的稀疏性,会造成计算上的浪费,所以在计算时采用逐位相乘再相加的方式进行:
由于矩阵的稀疏性,会造成计算上的浪费,所以在计算时采用逐位相乘再相加的方式进行:
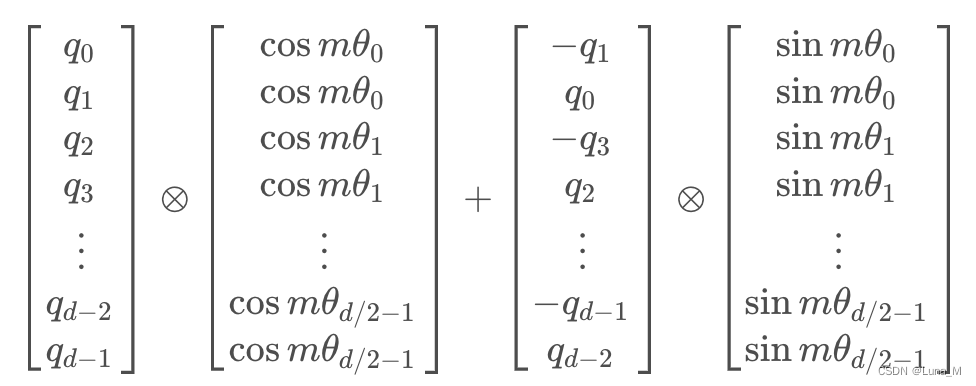
ALibi
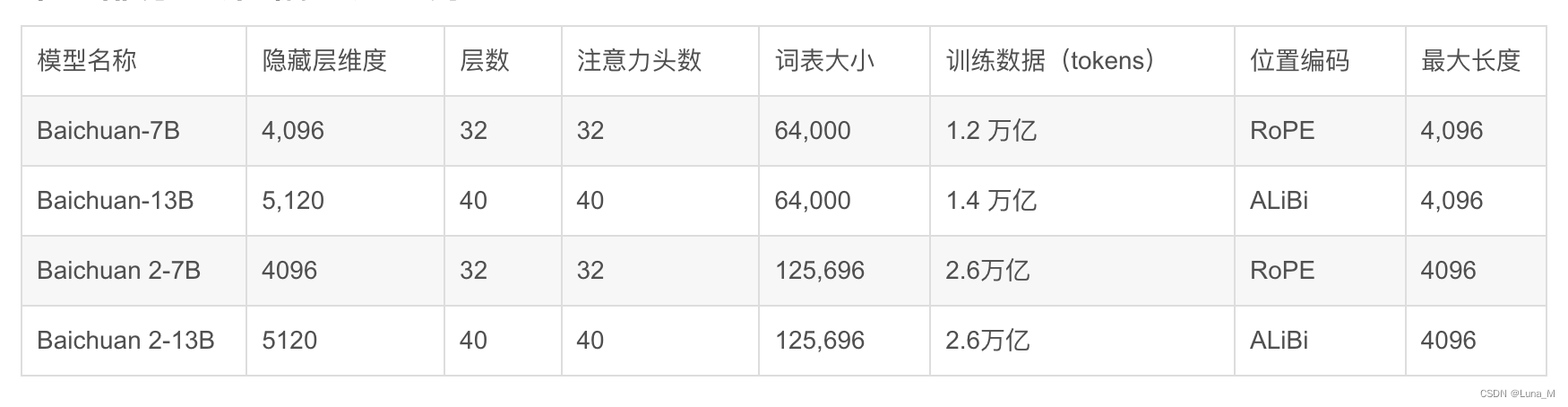 注意看上表的位置编码那一列,baichuan 7B无论第一代还是第二代,位置编码均用的RoPE,而baichuan 13B则无论是第一代还是第二代,均用的ALiBi
注意看上表的位置编码那一列,baichuan 7B无论第一代还是第二代,位置编码均用的RoPE,而baichuan 13B则无论是第一代还是第二代,均用的ALiBi
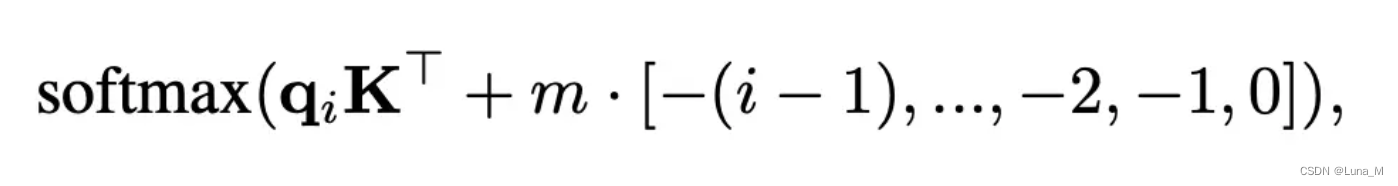
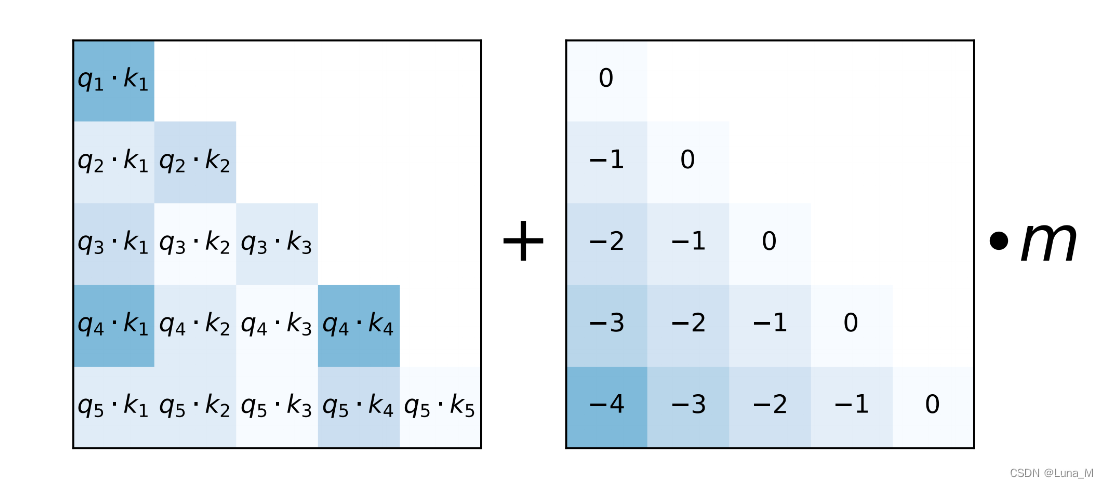
怎么理解呢,就是在query和key做矩阵点乘的基础上,加上一个常数负值,比如距离当前位置前1位为-1, 前两位为-2,这些常数要乘上 权重 m

7. LoRA
lora之前的PEFT方法是adapter/prefix/promp/P-tuning,但是Adapter会引入很强的推理延迟(只能串行),prefix/prompt/P-tuning很难练,而且要占用context length,变相的降低模型能力——所以,根本不改原来的model,这就引出了lora:Low-Rank Adaptation

初始化
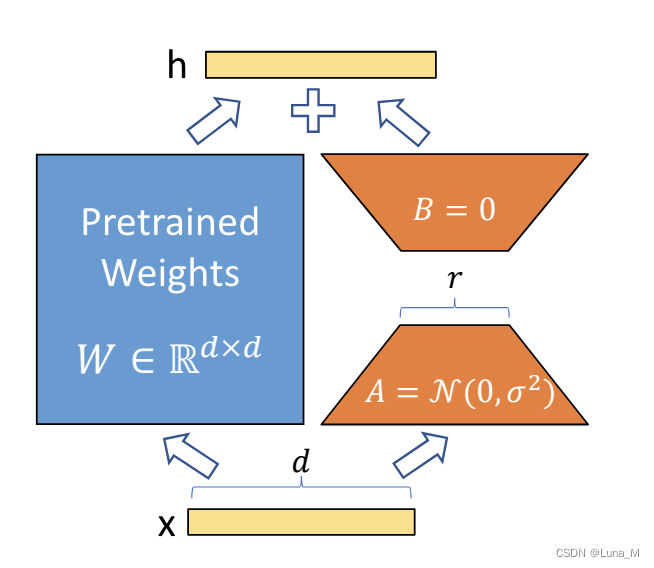
为什么用随机高斯分布初始化 A ,用 0 矩阵初始化 B ?
需要深入探讨这两个矩阵在权重更新过程中的角色和相互作用
- 矩阵𝐴:这个矩阵可以被看作是一个特征提取器,它将输入特征映射到一个低维空间(通过矩阵乘法)。在 LORA 的设置中,𝐴通常被视为首先应用于输入的一种转换,将数据从原始的高维空间压缩到一个低维空间。
- 矩阵𝐵:这个矩阵作为一个特征转换器,它将𝐴输出的低维表示映射回原始的高维空间。可以看作是从𝐴创建的低维空间中恢复信息到原始空间的过程。
为什么𝐴不能为零而 𝐵采用高斯初始化?
如果𝐴初始化为零,那么无论𝐵初始化为什么值,Δ𝑊始终为零矩阵。这意味着在训练的开始阶段,没有任何更新被应用于原始权重 𝑊,导致模型在这一阶段无法学习或适应任何新的特征或模式。
优点:
- 在面对不同的下游任务时,仅需训练参数量很少的低秩矩阵,而预训练权重可以在这些任务之间共享;
- 省去了预训练权重的梯度和相关的 optimizer states,大大增加了训练效率并降低了硬件要求;
- 训练好的低秩矩阵可以合并(merge)到预训练权重中,多分支结构变为单分支,从而达到没有推理延时的效果;
- 与之前的一些参数高效的微调方法(如 Adapter, Prefix-Tuning 等)互不影响,并且可以相互结合
局限性:
- 基于低秩的微调可能并不always work,比如finetune与pretrain的gap过大的时候,比如中英差异。当然,这一点在LLM时代可能并不突出,我们认为LLM在预训练阶段已经get了所有基本的知识,finetune只是格式微调,因此可能不会有上述gap过大的情况。
- 用lora也需要设置r和target module等,这部分超参的设置需要考虑
参考文献
大模型面试八股