1976、到达目的地的方案数
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大,将结果对 109 + 7 取余 后返回。
题目解析
本题要求用最少时间到达n-1的路径数目,所以有两个目标:找到最短用时路径、找到最短路径的所有数目。
关于找到最短路径,有很多种方式都可以找到,例如bfs、dijkstra。
而找路径数目,用到了动态规划的思想
假设v是从u点过来的
w a y s ( v ) = { w a y s [ u ] if 找到了一条新最短路 w a y s [ u ] + w a y s [ v ] if 距离相等则在原来的方案上加 ways(v) = \begin{cases} ways[u] & \text{if } 找到了一条新最短路 \\ ways[u] + ways[v] & \text{if } 距离相等则在原来的方案上加 \end{cases} ways(v)={ways[u]ways[u]+ways[v]if 找到了一条新最短路if 距离相等则在原来的方案上加
经验
在这样的设计中,我遇到了很多特别难以理解的问题:
存图
要保证双向的输入,一开始我的想法是只让小的节点指向大的节点,但后来发现:
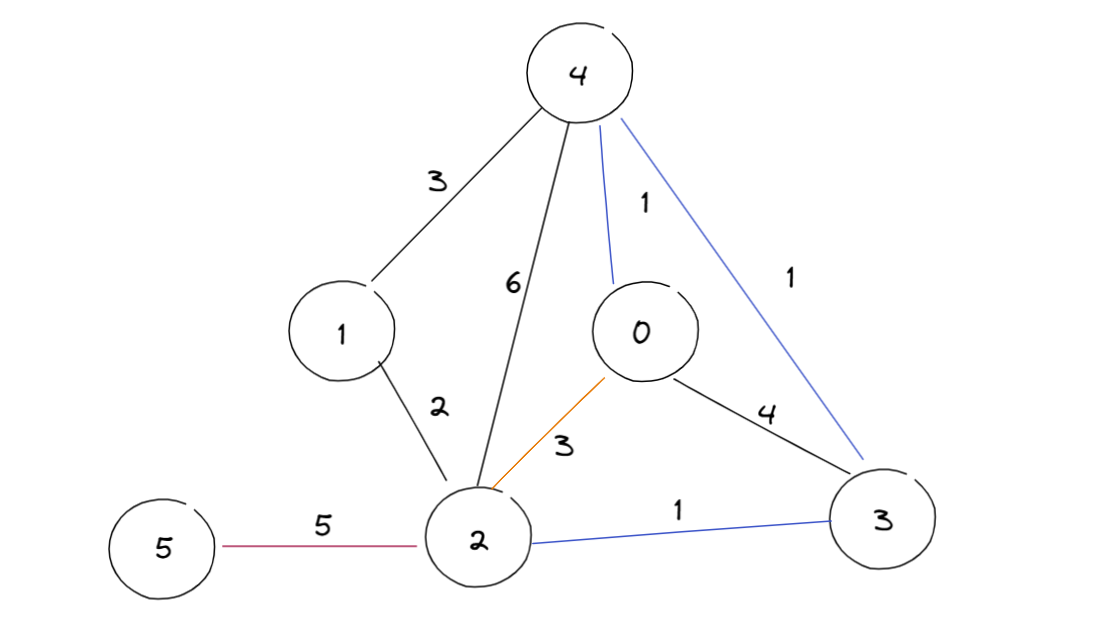
仍然有可能是先到4再到3,所以要把两个指向都加入进去。
必须使用priority_queue
为什么?因为是普通的queue,本质上是基于bfs来进行的搜索。而使用priority_queue的算法是dijkstra算法,这道题目不能用bfs最短路来求,
ways[u] + ways[v] 注意到这个递推公式,如果我们把 ways[v] 更新后,将这个节点后面的ways加上了ways[v] , 但后来又找到了v的一条等长最短路,导致ways[v]更新了,但他后面的节点没有更新。
如果是dijkstra算法,可以保证不会出现上面bfs的问题,因为他会按照时间排序,即保证 在将这个节点后面的ways加上了ways[v] 之后,不会找到等长或更小的最短路径的了,也就不会导致后面的节点不会更新。
参考代码
class Solution {
public:using LL = long long;const LL mod = 1e9+7;int countPaths(int n, vector<vector<int>>& roads) {vector<vector<pair<int,int>>> e(n);for(auto& road : roads){int x = road[0], y = road[1] , t = road[2];e[x].push_back({y,t});e[y].push_back({x,t});}vector<LL> dis(n, LLONG_MAX);//表示源到i点的最短距离vector<LL> ways(n);//表示源到点的最短的路径的数目//路径的长度,点的编号priority_queue<pair<LL,int>,vector<pair<LL,int>>, greater<pair<LL,int>>> q;q.emplace(0,0);dis[0] = 0;ways[0] = 1;while(!q.empty()){auto [t,u] = q.top();q.pop();for(auto& [v,w] : e[u]){if(t+w < dis[v]){cout << dis[v]<<endl;dis[v] = t+w;ways[v] = ways[u];q.push({dis[v] , v});}else if(t+w == dis[v]){ways[v] = (ways[u] + ways[v]) % mod;}}}return ways[n-1];}
};