C#二维数组(矩阵)求伴随矩阵和逆矩阵

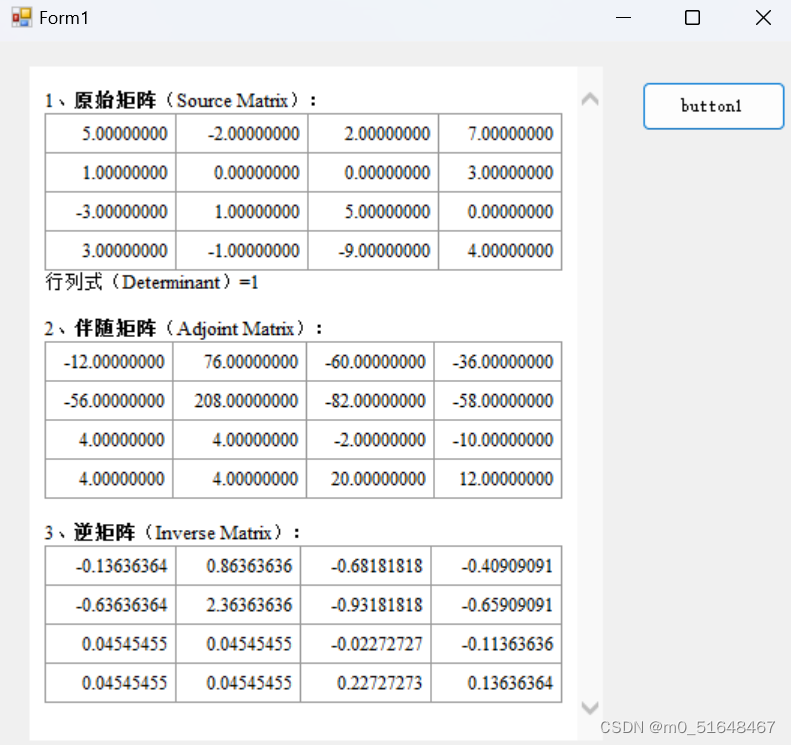
程序框架及winform窗体

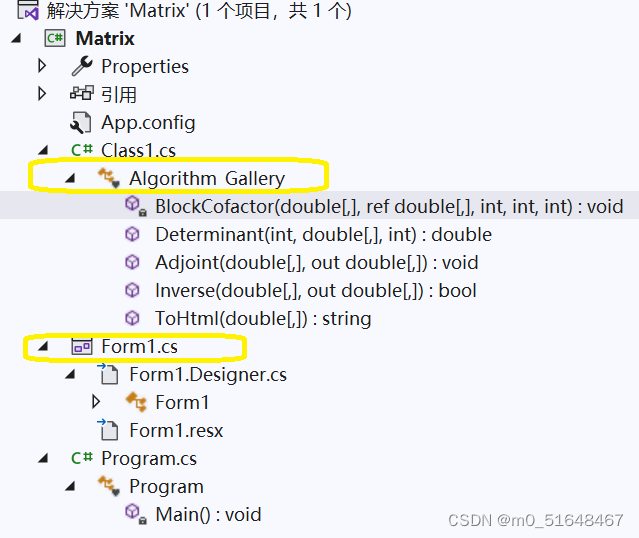
窗体控件:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace Matrix
{internal class Algorithm_Gallery{// <summary>/// 计算 A[p,q] 位于 [,]temp 的块辅因子/// </summary>/// <param name="matrix"></param>/// <param name="temp"></param>/// <param name="p"></param>/// <param name="q"></param>/// <param name="n"></param>private static void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n){//从一个给定的二维数组（matrix）中提取除了第p行和第q列之外的所有元素，并将这些元素填充到另一个二维数组（temp）中if (temp.GetLength(0) != n - 1 || temp.GetLength(1) != n - 1)//temp数组应该是一个(n-1) * (n-1)的二维数组{throw new ArgumentException("The size of temp array is not (n-1) x (n-1).");}int i = 0;int j = 0;for (int row = 0; row < n; row++){for (int col = 0; col < n; col++){if (row != p && col != q){temp[i, j++] = matrix[row, col];//如果当前遍历的行不是第p行且列不是第q列，则将matrix中的该元素赋值给temp。if (j == (n - 1)){j = 0;i++;//每当列索引j等于n-1时（即到达当前行的最后一个位置），重置j为0并将i加1，以便在下一行开始填充元素}}}}}/// <summary>/// 求矩阵行列式（递归算法）/// </summary>/// <param name="N"></param>/// <param name="matrix"></param>/// <param name="n"></param>/// <returns></returns>public static double Determinant(int N, double[,] matrix, int n){//计算一个给定二维数组（matrix）的行列式（determinant）if (n == 1){return matrix[0, 0];}double D = 0.0;double[,] temp = new double[n-1, n-1];int sign = 1;for (int f = 0; f < n; f++){BlockCofactor(matrix, ref temp, 0, f, n);D += sign * matrix[0, f] * Determinant(N, temp, n - 1);sign = -sign;}return D;}/// <summary>/// 伴随矩阵/// </summary>/// <param name="A"></param>/// <param name="adj"></param>public static void Adjoint(double[,] matrix, out double[,] adjoint){int N = matrix.GetLength(0);adjoint = new double[N, N];if (N == 1){adjoint[0, 0] = 1.0;return;}int sign = 1;double[,] temp = new double[N-1, N-1];for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){BlockCofactor(matrix, ref temp, i, j, N);sign = ((i + j) % 2 == 0) ? 1 : -1;adjoint[j, i] = (sign) * (Determinant(N, temp, N - 1));}}}// <summary>/// 矩阵求逆/// </summary>/// <param name="A"></param>/// <param name="inverse"></param>/// <returns></returns>public static bool Inverse(double[,] matrix, out double[,] inverse){int N = matrix.GetLength(0);inverse = new double[N, N];double det = Determinant(N, matrix, N);if (det == 0){return false;}Adjoint(matrix, out double[,] adj);for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){inverse[i, j] = adj[i, j] / (double)det;}}return true;}public static string ToHtml(double[,] y){int m = y.GetLength(0);int n = y.GetLength(1);StringBuilder sb = new StringBuilder();sb.AppendLine("<style>");sb.AppendLine("td { padding:5px;text-align:right; }");sb.AppendLine("</style>");sb.AppendLine("<table width='100%' border=1 bordercolor='#999999' style='border-collapse:collapse;'>");for (int i = 0; i < m; i++){sb.AppendLine("<tr>");for (int j = 0; j < n; j++){sb.AppendLine("<td>" + String.Format("{0:F8}", y[i, j]) + "</td>");}sb.AppendLine("</tr>");}sb.AppendLine("</table>");return sb.ToString();}}
}

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;namespace Matrix
{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e){double[,] A = {{5, -2, 2, 7},{1, 0, 0, 3},{-3, 1, 5, 0},{3, -1, -9, 4}};double[,] b = new double[3, 3] { { 1, 2, 3 }, { 0, 1, 4 }, { 5, 6, 0 } };double d = Algorithm_Gallery.Determinant(0, b, 3);StringBuilder sb = new StringBuilder();//sb.Append(Welcome());sb.AppendLine("1、<b>原始矩阵</b>（Source Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(A));sb.AppendLine("行列式（Determinant）=" + d + "<br>");Algorithm_Gallery.Adjoint(A, out double[,] adj);sb.AppendLine("<br>2、<b>伴随矩阵</b>（Adjoint Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(adj));Algorithm_Gallery.Inverse(A, out double[,] inv);sb.AppendLine("<br>3、<b>逆矩阵</b>（Inverse Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(inv));//sb.Append(Bye());webBrowser1.DocumentText = sb.ToString();}}
}

运行--点击button1: