控制系统时域分析
(1)稳定性分析
稳定是控制系统的重要性能,也是系统设计过程中的首要问题。线性系统稳定的充分必要条件是:闭环系统特征方程的所有根均具有负实部。在MATLAB中可以调用roots命令求取特征根,进而判别系统的稳定性。
命令格式:
p=roots(den)
其中,den为特征多项式降幂排列的系数向量;p为特征根。
(2)动态性能分析
1)单位脉冲响应
命令格式:
y=impulse(sys,t)当不带输出变量y时,impulse命令可直接绘制脉冲响应曲线;t用于设定仿真时间,可缺省。
2)单位阶跃响应
命令格式:
y=step(sys,t)当不带输出变量y时,step命令可直接绘制阶跃响应曲线;t用于设定仿真时间,可缺省。
3)任意输入响应
命令格式:
y=lsim(sys,u,t,x0)当不带输出变量y时,lsim命令可直接绘制响应曲线;其中u表示输入,x0用于设定初始状态,缺省时为0,t用于设定仿真时间,可缺省。
4)零输入响应
命令格式:
y= initial(sys,x0,t)
initial命令要求系统sys为状态空间模型。当不带输出变量y时,initial命令可直接绘制响应曲线;t用于设定仿真时间,可缺省。
系统性能复频域分析
(1)绘制零、极点分布图
命令格式:
[p,z]=pzmap(sys)
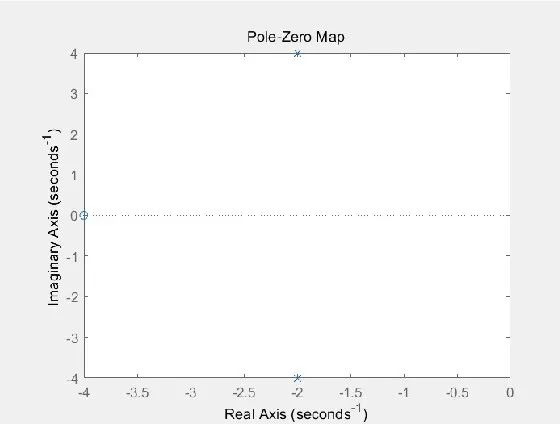
当不带输出变量[p,z]时,pzmap命令可直接在复平面内标出传递函数的零、极点。在图中,极点用“×”表示,零点用“o”表示。
例:
num=[1,4];
den=[1,4,20];
sys=tf(num,den);
pzmap(sys)其运算结果如图:
(2)绘制根轨迹图
利用MATLAB绘制根轨迹的一般步骤如下:
1)先将特征方程写成1+Kp(s)/q(s)=0的形式,其中K为所研究的变化参数,得到等效开环传递函数G=p(s)/q(s)
2)调用rlocus命令绘制根轨迹
命令格式:

解:由题意,系统闭环特征多项式为
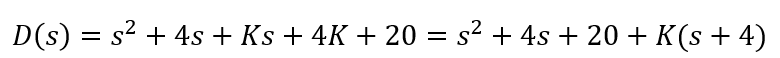
等效开环传递函数
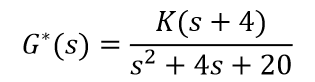
调用pzmap和rlocus命令绘制零、极点分布图和根轨迹图
num-[1,4];
den-[1,4,20];
G=tf(numm,den);%建立等效开环传递函数模型
figure(1)
pzmap(G);%绘制零、极点分布图
figure(2)
rlocus(G);%绘制根轨迹其运算结果如图:
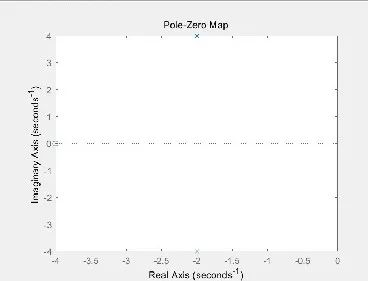
图零极点分布图
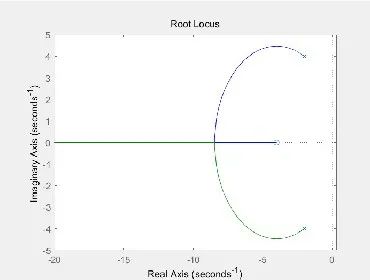
图根轨迹分布图
为了计算系统临界阻尼时对应的K值和相应的闭环极点,可调用rlocfind命令。
命令格式:
rlocfind(G) %确定增益及其相应的闭环极点执行rlocfind命令后,MATLAB将在根轨迹图上出现“+”提示符,通过鼠标提示符移到根轨迹上相应的位置,然后按回车键,于是所选闭环极点及其对应的参数K就会在命令行中显示。其结果为:
K=12.9443,s=-8.47
控制系统的频域分析
(1)伯德图
命令格式:
[mag,phase,w]=bode(sys)当缺省输出变量时,bode命令可直接绘制伯德图;否则,将只计算幅值和相角,并将结果分别存放在向量mag和phase中,频率为w。
margin命令也可以绘制伯德图,并直接得出幅值裕度、相角裕度及其对应的截止频率、穿越频率。
命令格式:
[Gm,Pm,Wcg,Wcp]=margin(sys)当缺省输出变量时,margin命令可直接绘制伯德图;并将幅值裕度和相角裕度及其对应的截止频率、穿越频率标注在图形标题端。
(2)尼柯尔斯图
命令格式:
[mag,phase,w]=nichols(sys)当缺省输出变量时,nichols命令可直接绘制尼柯尔斯图。
(3)奈奎斯特图
命令格式:
[re,im,w]=nyquist(sys)当缺省输出变量时, nyquist命令可直接绘制奈奎斯特图。