---

第1关：数据读取与合并

任务描述
本关任务：加载 csv 数据集，实现 DataFrame 合并。

知识讲解
Pandas 模块导入
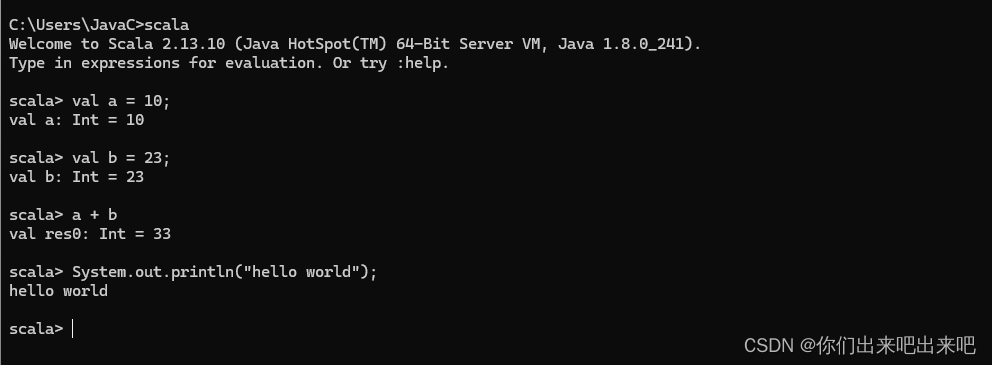
import pandas as pd

读取 csv 文件
In [1]: pd.read_csv(path) #返回DataFrame
index_col 是 read_csv 方法的常用参数，常用作读取文件的指定列为行索引。例如有数据文件 test.csv ，其内容为：

name,a,b,c
x,1,2,3
y,4,5,6
把第 0 列作为行索引的代码如下：

In [1]: df = pd.read_csv('test.csv',index_col = 0)#df的行索引就是test.csv的第0列。
In [2]: df.index
Out[2]: Index(['x', 'y'], dtype='object', name='name')
In [3]: df.values
Out[3]:
array([[1, 2, 3],[4, 5, 6]], dtype=int64)
In [4]: df.columns
Out[4]: Index(['a', 'b', 'c'], dtype='object')

DataFrame合并
DataFrame 合并有三种方法：concat 、 append 和 merge 。

详情参见教材和官方文档。

注意：若出现如下错误，直接添加参数 sort=True 即可。
“
To accept the future behavior, pass ‘sort=True’.
……
编程要求
根据提示，在右侧编辑器补充代码，完成本关任务。

测试说明
平台会对你的代码进行测试，若与预期输出一致，则算通关。
示例代码如下：

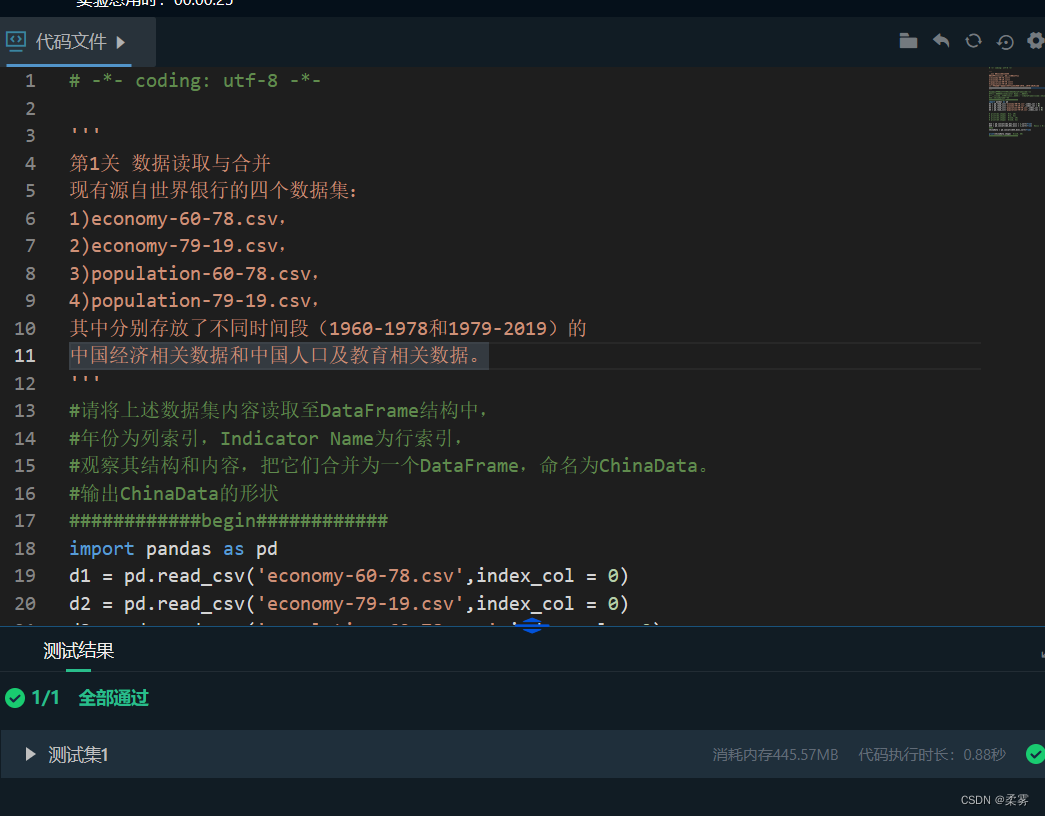
# -*- coding: utf-8 -*-'''
第1关 数据读取与合并
现有源自世界银行的四个数据集：
1)economy-60-78.csv，
2)economy-79-19.csv，
3)population-60-78.csv，
4)population-79-19.csv，
其中分别存放了不同时间段（1960-1978和1979-2019）的
中国经济相关数据和中国人口及教育相关数据。
'''
#请将上述数据集内容读取至DataFrame结构中，
#年份为列索引，Indicator Name为行索引，
#观察其结构和内容，把它们合并为一个DataFrame，命名为ChinaData。
#输出ChinaData的形状
############begin############
import pandas as pd
d1 = pd.read_csv('economy-60-78.csv',index_col = 0)
d2 = pd.read_csv('economy-79-19.csv',index_col = 0)
d3 = pd.read_csv('population-60-78.csv',index_col = 0)
d4 = pd.read_csv('population-79-19.csv',index_col = 0)# print(d1.shape)  #(2, 19)
# print(d2.shape)  #(2, 41)
# print(d3.shape)  #(116, 19)
# print(d4.shape)  #(116, 41)d12 = pd.concat([d1,d2],axis = 1,sort=True)
d34 = pd.concat([d3,d4],axis = 1,sort=True)  #axis = 0为纵向拼接，axis = 1为横向拼接。
ChinaData = pd.concat([d34,d12],sort=True)print(ChinaData.shape)  #(119, 60)
#############end#############

第2关：数据清洗

任务描述
本关任务：数据清洗
包括：空白行删除、数据完整性检验、数据填充、插值等内容。

相关知识
为了完成本关任务，你需要掌握：

删除缺失值；
检测缺失值；
填充缺失值；
拉格朗日插值；
线性插值。
删除缺失值
DataFrame.dropna 方法用于删除含有缺失值的行或列，关键参数：axis 和how。

axis
表示轴向，0 为行，1 为列，默认 0。

how
表示删除形式，how = ‘any’ 表示只要有缺失值就删除；how=‘all’ 表示全为缺失值才删除。

检测缺失值
DataFrame.isnull() 识别缺失值，返回包含True和False的 DataFrame。
DataFrame.notnull() 方法识别非缺失值，返回包含True和False的 DataFrame。
上述两方法结合 sum 函数可用于检测数据序列中缺失值的分布情况。

填充缺失值
DataFrame.fillna 方法能用指定值替换缺失值。关键参数：value、method和axis。

value
表示指定的填充值。

method
method = 'bfill’后向填充，用后面的非缺失值填充；
method = 'ffill’前向填充，用前面的非缺失值填充。

axis
表示操作轴向，默认1（列）。

拉格朗日插值

from scipy.interpolate import lagrange
formula = lagrange(x,y)#formula是通过lagrange方法生成的公式，x和y为数据序列
ins_y = formula(ins_x)#ins_x为缺失值所在位置，ins_y为插值结果。

线性插值

from scipy.interpolate import interp1d#1是数字一
formula = interp1d(x,y,kind = 'linear')#formula是通过linear方法生成的公式，x和y为数据序列
ins_y = formula(ins_x)#ins_x为缺失值所在位置，ins_y为插值结果。

编程要求
根据提示，在右侧编辑器补充代码，完成本关任务。

测试说明
平台会对你的代码进行测试，若与预期输出一致，则算通关。

开始你的任务吧，祝你成功！

示例代码如下：

# -*- coding: utf-8 -*-
'''
第2关 数据清洗
'''
import pandas as pd
d1 = pd.read_csv('economy-60-78.csv',index_col = 0)
d2 = pd.read_csv('economy-79-19.csv',index_col = 0)
d3 = pd.read_csv('population-60-78.csv',index_col = 0)
d4 = pd.read_csv('population-79-19.csv',index_col = 0)
d12 = pd.concat([d1,d2],axis = 1,sort=True)
d34 = pd.concat([d3,d4],axis = 1,sort=True)
ChinaData = pd.concat([d34,d12],sort=True)
'''
请针对ChinaData完成如下操作。
'''
# 2.1 删除空白行
# 提示：dropna,inplace
############begin############
print('原表形状',ChinaData.shape)
linenum = ChinaData.shape[0]
ChinaData.dropna(how='all',inplace=True)
print('新表形状',ChinaData.shape)
linenum -=ChinaData.shape[0]
print("%d个空白行被删除。"%linenum)
#############end############## 2.2 查找数据最完整（空值最少）的年份并输出
# 提示：notnull(),根据值找索引（上课讲过的方法）
############begin############
#print(ChinaData.notnull().sum().sort_values(ascending=False)[0])
nullsummary = ChinaData.isnull().sum()
y = nullsummary.loc[nullsummary==nullsummary.min()].index[0]
print(y)#############end############## 2.3 前向填充"男性吸烟率（吸烟男性占所有成年人比例）"，输出2000年至2019年的数据
# fillna,ffill
############begin############cigarette = ChinaData.loc['男性吸烟率（吸烟男性占所有成年人比例）',:]
print(cigarette.fillna(method = 'ffill').loc['2000':'2019'])#############end############## 2.4 用2015年到2018年4年的gdp数据对2019年GDP数值进行拉格朗日插值预测，输出预测结果
# lagrange,
# 注意：x的取值从0开始，即x = np.array([0,1,2,3])，代表2015至2018 4年，2019年的x取值为4。
############begin############from scipy.interpolate import lagrange
gdp = ChinaData.loc['GDP',:]
lagf = lagrange(range(0,4),gdp.values[-5:-1])
print(lagf(4))
#############end############## 2.5 用线性插值法填充“入学率，高等院校，男生（占总人数的百分比）”1995年到2002年数据,并输出插值后的94年至03年的数据
# interp1d
############begin############from scipy.interpolate import interp1d
student = ChinaData.loc['入学率，高等院校，男生（占总人数的百分比）',:]
linevalue = interp1d([0,9],[student.loc['1994'],student.loc['2003']],kind = 'linear')
student.loc['1995':'2002'] = linevalue(range(1,9))
print(student.loc['1994':'2003'])#############end#############

第3关：数据转换

任务描述
本关任务：数据转换。包括数据标准化和数据离散化。

知识讲解
为了完成本关任务，你需要掌握：1、离差标准化，2、等宽离散化。

离差标准化
离差标准化就是对原始数据进行线性变换并映射至 [0，1] 区间的方法。该方法需要自行编写实现函数，建议参考教材或网络资源自行实现。

等宽离散化
等宽离散化将数据的值域分成宽度相同区间，根据数据所在区间取值，实现连续变量的离散化。pandas.cut函数可以实现这种操作，关键参数：x和bins。

x
待离散化的数据。

bins
离散化类别数。

注意：
获得离散化结果后，常用value_counts()方法对离散化结果进行频数统计，以观察离散化数据的分布情况。

编程要求
根据提示，在右侧编辑器补充代码，完成本关任务。

测试说明
平台会对你的代码进行测试，若与预期输出一致，则算通关。

开始你的任务吧，祝你成功！

示例代码如下：

# -*- coding: utf-8 -*-'''
第3关 数据转换
'''
import pandas as pd
d1 = pd.read_csv('economy-60-78.csv',index_col = 0)
d2 = pd.read_csv('economy-79-19.csv',index_col = 0)
d3 = pd.read_csv('population-60-78.csv',index_col = 0)
d4 = pd.read_csv('population-79-19.csv',index_col = 0)
d12 = pd.concat([d1,d2],axis = 1,sort=True)
d34 = pd.concat([d3,d4],axis = 1,sort=True)
ChinaData = pd.concat([d34,d12],sort=True)
'''
请针对ChinaData实现下列操作
'''
# 3.1 对“人口，总数”数据（1960-2018）进行离差标准化，并输出。
# 提示：自定义离差标准化函数，注意统计年份区间
############begin############def MinMaxScale(data):data = (data-data.min())/(data.max()-data.min())return data
population = ChinaData.loc['人口，总数',:][:-1]
npopu = MinMaxScale(population)
print(npopu)#############end############## 3.2 对“GDP 增长率（年百分比）”（1961-2018）数据进行等宽离散化为7类，输出分布情况
# 提示：cut，注意统计年份区间
############begin############gdpRatio = ChinaData.loc['GDP 增长率（年百分比）',:][1:-1]
result = pd.cut(gdpRatio,7)
print(result.value_counts())#############end#############

---