目录

第2章  数学基数    

2.1 预备知识

2.1.1 素数

2.1.2 模运算

2.1.3 群

【定义2-2】（群的定义）

【定义2-3】（交换群）

【定义2-4】（单位元）

【定义2-5】（逆元）

【定义2-6】（阶）

【定义2-7】（循环群）

    2.2 密码学困难性假设

    2.2.1 大数分解困难性假设

2.2.2 离散对数困难性假设

2.2.3 Diffie-Hellman问题

个人总结：

素数：

模运算：

群论：

困难性假设：

Diffie-Hellman问题

---

第2章  数学基数    

        现代密码学是建立在数学、计算机科学等基础学科之上的。《老子·德经》有云：合抱之木，生于毫末；九层之台，起于累土；千里之行，始于足下。本章介绍现代密码学中的一些常用数学基础知识。

2.1 预备知识

2.1.1 素数

        整数集合Z用表示，对于整数集合中的元素a,b∉Z，如果存在一个整数c，使得a*c=b成立，则称a整除b，记作a|b。如果a|b并且a是正整数，则称a是b的一个除数。如果加上条件a∉{1,b}，则称a是b的一个非平凡除数或称为因子。正整数p＞1如果没有因子，则为素数；也就是说，素数只有1和自身两个除数。一个大于1的正整数如果不是素数则为合数。我们约定1既不是素数也不是合数。
很多密码学协议中都需要生成素数。生成一个小的素数比较容易，然而基于小素数的密码学协议往往是不安全的。如何生成一个大素数？我们可以选择一个较大的数，然后检查这个数是否为素数，如果不是，则重新选择并检查，直到产生一个大素数为止。下面介绍著名的RM素数检测算法。
                                        【算法2-1】 RM素数检测算法
        步骤1：对于待检测的随机数p，计算b。b是2整除p−1的次数，即2b 是能整除p−1的2的最大幂数。然后计算m，使得n=1+2b m。
        步骤2：选择一个小于p的随机数a。
        步骤3：设j=0且z=am mod p。
        步骤4：如果z=1或z=p−1，那么p通过测试，p可能是素数。
        步骤5：如果 j﹥0且z=1，那么p不是素数。
        步骤6：设j=j+1。如果j﹤6且z≠p−1，则计算z=z2  modp，然后回到步骤5。如果z=p−1，那么p通过测试，p可能是素数。
        步骤7：如果j=b且z≠p−1，那么p不是素数。

2.1.2 模运算
 

【定义2-1】（同余的模）
        设a,b是整数，如果a=b+kn对某些k成立，那么就说a,b模n同余，记作a≡b（modn），n称为同余的模。
        模n运算的结果一定是0到n−1之间的一个数，从0到n−1的整数组成的集合包括了模n的所有结果，或者说模n运算的结果一定落在这个集合中，称这个集合为模n运算的最小剩余集，记作Zn
 ={0,1,2,…,n−1}。

2.1.3 群

【定义2-2】（群的定义）

一个非空集合G对于一个二元运算“*”来说作为一个群，假如
Ⅰ.G对于“*”来说是闭的；
Ⅱ.结合律成立，即对于G的任意三个元a、b、c满足
                                        a*（b*c）=（a*b）*c
Ⅲ.G中至少存在一个左单位元e，使得
                                                e *a=a
Ⅳ.对于G的每一个元a，在G中至少存在一个左逆元a−1 ，使得
                                                a− 1 *a=e
例如，假设G是全体整数的集合，G对于普通加法来说作成一个群。假设G是所有不等于零的整数的集合，G对于普通乘法来说不作成一个群。
一个群G中元素的个数可以是有限的，也可以是无限的。如果一个群中元素的个数是一个有限整数，则称这个群为有限群。否则的话，这个群称为无限群。一个有限群的元的个数称为这个群的阶。由于在一个群里结合律是成立的，因此a1*a2*…*an有意义。又由于群对于“*”来说是闭的，因此a1*a2*…*an

 是G的某一个元。这样，可以把n个相同的元a来相乘。因为用普通乘法的符号来表示群的运算，所以可以使用符号an来表示n个相同的元a的乘法，即
                                an =a∗a∗…∗a（n是正整数）
并且也把a称为a的n次乘方（简称n次方）。

【定义2-3】（交换群）

一个群G称为交换群，假如
                                a*b=b*a
对于G的任何两个元a、b都成立。

【定义2-4】（单位元）

一个群G中唯一能使
                                e*a=a*e=a　　　　　　　 （a是G的任意元）
的元e称为群G的单位元。

【定义2-5】（逆元）

唯一能使
a− 1*a=a*a−1 =e
的元a−1称为元 a的逆元，有时也简称逆。

【定义2-6】（阶）

对于群G的一个元a，能够使得
                                am=e

的最小的正整数m称为a的阶。

【定义2-7】（循环群）

如果一个群G的每一个元都是G的某一个固定元a的乘方，就把G称为循环群；也就是说，G是由元a所生成的，并且用下面符号来表示
                                        G= （a）
其中，a称为G的一个生成元。

    2.2 密码学困难性假设

            现代密码学方案尤其是公钥密码学方案的安全性是建立在解决某些问题的困难性假设基础上的。例如，RSA公开密钥算法是基于大数分解困难性假设设计的，ElGamal加密算法是基于离散对数困难性假设设计的，Paillier加密算法的安全性依赖于合数剩余判定困难性假设。那么，在密码学中什么样的问题是困难的呢？困难并不是无法计算或无法攻破，很多学者致力于研究当前密码学中常用困难性假设问题的解决算法并已经取得了一系列进展。例如，对于满足如下假设的大数分解困难性问题，已经陆续有更短运行时间的算法被提出。假设N=pq，p和q是两个长度相等但大小不同的素数，大数分解问题要求对N进行分解，即求出N的素因子。Pollard提出的RHO方法是一种通用因子分解方法，针对上述大数分解问题，该算法的时间复杂度是n的指数函数，其中n是大数N的长度。Pomerance提出的二次筛算法也是一种通用因子分解方法，该算法的时间复杂度是n的亚指数函数。尽管解决这些困难性假设问题已经取得了一些成果，但是当前没有找到多项式时间算法或概率多项式时间算法来解决这些问题。因此，当合理选择参数时，人们认为攻破基于这些困难性问题的密码学方案在时间上是不可接受的，从而保证了这些密码学方案在一段时间之内的安全性。当然，随着信息技术的不断进步，如果有一天这些困难性假设不再成立，那么这些假设所对应的密码学方案的安全性也将荡然无存。
    本节介绍现代密码学方案中常用的困难性假设问题，深入理解这些问题可以帮助人们更好地设计密码学方案。

    2.2.1 大数分解困难性假设

        在数论中，对一个数进行因子分解是一个古老的问题。分解一个小的数相对比较容易，例如下面使用试除法得到一个数的因子分解，其中pi 是互不相等的素数并且xi ≥1。
                                      12=22×3

        然而，分解一个较大的数就不是这么容易了。尽管当前已经有二次筛算法、连分式算法、普通数域筛选法等一系列研究成果，但是正如上文中提到的，这些算法无法在多项式时间或概率多项式时间内解决问题。因此，在当前的计算能力下，解决大数分解问题是困难的。这就是大数分解困难性假设，其形式化定义如下。
给定一个大数N,N满足N=pq，其中p和q是两个长度相等但大小不等的素数，即 。对于任意的多项式时间算法A（N）=（p′,q′），存在一个可忽略的函数neg（n）满足

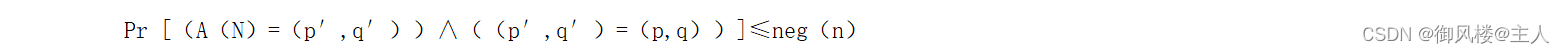
2.2.2 离散对数困难性假设

        首先解释什么是离散对数。给定素数p，假设α是上的生成元，β是上的元素，如果整数x满足αxmod p=β，则称x是关于α底β的对数，记作x log=αβ。下面讨论定义在任意循环群上的离散对数。假设G是n阶循环群，g是G上的生成元，则对于任意的h∈G，存在唯一x∈Zn使得gx=h。当循环群G已知时，称x是关于g底h的对数，记作x=loggh。可以看出，对于任意整数x′，如果gx′=h，则x=x′modn。从这个角度来讲，离散对数的值在“有限”范围内，而传统对数值的范围是无穷集合。尽管存在这种差别，但是传统对数的很多规则仍然适用于离散对数。例如，假设e是循环群 G的单位元，则logge=0。

        严格的离散对数困难性假设如下：假设p是一个大素数且|p|=l,a∈是一个生成元，β∈且满足αxmod p=β。对于任意的多项式时间算法A（α,β,p），存在一个可忽略的函数neg（n）满足

循环群上的离散对数困难性假设如下：给定n阶循环群 G,g是 上的生成元，h是 G上的元素。对于任意的多项式时间算法A(G,g,h) ，存在一个可忽略的函数neg（n）满足

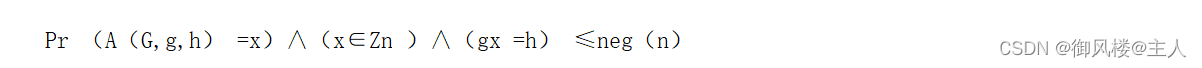
2.2.3 Diffie-Hellman问题

        Diffie-Hellman 问题与上节介绍的离散对数困难性假设具有一定的相关性。常用的Diffie-Hellman问题分为两类，一类是计算Diffie-Hellman问题，简称CDH；另一类是判定Diffie-Hellman问题，简称DDH。给定n阶循环群G ,g是G 上的生成元，h1 和h2都是G 上的元素。计算Diffie-Hellman问题是指计算。判定 Diffie-Hellman 问题是指判定 上的元素h′是否满足 。

个人总结：

1. 素数：

   1. 素数就是只能被1和自身整除的数，比如2、3、5、7等等。在密码学中，我们常常需要用到大的素数来确保密码的安全性。

2. 模运算：

   1. 就像时钟一样，当我们说12点加5小时等于5点，这就是模12的运算。在密码学中，我们用模运算来处理数字，确保它们在一个固定的范围内。

3. 群论：

   1. 想象一下一个团队，里面的成员可以互相合作完成任务。群论就是研究这种合作的数学理论。在密码学中，我们利用群论来描述密码系统中的运算规则和密钥生成过程。

4. 困难性假设：

   1. 这是一种假设，认为某些数学问题很难在合理的时间内解决。例如，将一个大数分解成素数，或者找到离散对数问题的解。密码学方案的安全性建立在这些问题的困难性之上。

5. Diffie-Hellman问题

通过一个简单的例子来说明Diffie-Hellman问题。

假设有两个人，Alice 和 Bob，他们想要在不安全的网络上进行加密通信，但他们不希望其他人知道他们的密钥。

1. 首先，他们选定一个质数 \(p\) 和一个基数 \(g\)。例如，他们选择了 \(p = 23\) 和 \(g = 5\)。

2. 接下来，他们各自选择一个私密数字。例如，Alice 选择了 \(a = 6\)，而 Bob 选择了 \(b = 15\)。

3. 然后，他们利用选定的公共 \(p\) 和 \(g\)，以及各自的私密数字 \(a\) 和 \(b\)，计算出一个公开的值。Alice 计算 \(A = g^a \mod p\)，而 Bob 计算 \(B = g^b \mod p\)。

4. 现在，Alice 和 Bob 交换他们计算出的公开值 \(A\) 和 \(B\)。

5. 最后，他们各自使用对方发送的公开值和自己的私密数字计算出共享密钥。Alice 计算 \(K = B^a \mod p\)，而 Bob 计算 \(K = A^b \mod p\)。

现在，Alice 和 Bob 都拥有了同一个共享密钥 \(K\)，但其他人却很难通过公开的值 \(A\)、\(B\) 和 \(p\)、\(g\) 推断出这个密钥。这就是 Diffie-Hellman 问题的基本思想：通过利用数学运算，让双方安全地生成共享密钥，从而保护通信安全。

        本文所包含的内容系《现代密码学——基于安全多方计算协议的研究》一书。这些内容的目的是为了学术交流和个人学习，并且在此过程中尊重原作者的知识产权。特此对作者的辛勤工作表示感谢，并感谢他们为密码学领域做出的贡献。如有侵权行为，请及时联系我进行删除或修改。感谢您对知识产权的尊重与支持。