算法简介
Otsu阈值法,也被称为大津算法,是一种在图像处理中广泛使用的自动阈值分割技术。这种方法由日本学者大津展之于1979年提出,旨在根据图像的灰度直方图来自动选择最佳全局阈值。Otsu阈值法的核心思想是最小化类内方差或最大化类间方差。
以下是Otsu阈值法的一般步骤:
-
预处理:对输入图像进行预处理,以减少噪声和增强图像特征。常见的预处理方法包括高斯平滑滤波,这有助于平滑图像,减少随机噪声。
-
灰度直方图:计算图像的灰度直方图,即统计图像中每个灰度级出现的频率。直方图可以提供图像的灰度分布信息。
-
阈值计算:这是Otsu算法的关键步骤。算法通过遍历所有可能的阈值,计算每个阈值对应的类间方差与类内方差之比。Otsu的目标是找到一个阈值,使得这个比值最大化。类内方差最小化意味着阈值两边的像素点尽可能相似,而类间方差最大化意味着阈值两边的像素点差异尽可能大。
-
二值化:使用计算得到的阈值T对原图像进行二值化处理。所有小于或等于阈值T的像素点被设置为背景像素(例如0),而所有大于阈值T的像素点被设置为前景像素(例如255)。
Otsu阈值法的优点在于它的简单性和有效性,特别是在对比度较高的图像中。然而,对于具有复杂背景或光照不均的图像,这种方法可能不够准确。在这些情况下,可能需要更高级的阈值技术或结合其他图像处理技术来获得更好的分割效果。
由于您提供的链接无法解析,如果您需要关于Otsu阈值法的更多信息或有其他相关问题,请告知,我会尽力帮助您。
算法的逻辑
双峰图像(bimodal images)的像素直方图具有两个明显的峰值,这通常意味着图像中存在两种明显不同的像素强度区域,这些区域分别对应于图像中的前景和背景。在这类图像中,前景和背景在灰度或颜色上有明显的区分,因此使用Otsu阈值法可以有效地将它们分开。
双峰直方图的特点是:
-
两个峰值:直方图有两个明显的峰值,分别代表图像中的前景和背景的像素强度分布。
-
低谷:在两个峰值之间存在一个低谷,这个低谷的位置可以作为潜在的阈值,用于区分前景和背景。
-
对比度:两个峰值之间的对比度越高,使用Otsu阈值法的效果通常越好,因为这意味着前景和背景之间的区分度更高。
Otsu算法的核心思想正是利用这种双峰分布的特性,通过最大化类间方差来确定最佳阈值。类间方差衡量的是前景和背景两个类别之间的差异性,而类内方差衡量的是类别内部的一致性。Otsu算法寻找的阈值能够最大化类间方差与类内方差的比值,从而实现最佳的前景和背景分离。

如下就是一个双峰图像的示例:

假设一副灰度图,像素值灰度级为,如我们常见的灰度图像,灰度级是256。
像素值为第个灰度级的像素点有个,则这幅图像总的像素点个数为 N = n 1 + n 2 + . . . n L N=n_1 + n_2 + ...n_L N=n1+n2+...nL
基于上述假设,某个像素点为灰度级的概率可表示为:
p i = n i N p_{i}\,=\,\frac{n_{i}}{N} pi=Nni
满足以下条件:
p i > 0 , ∑ i = 1 L p i = 1 p_{i}\gt 0,\sum_{i=1}^{L}p_{i}=1 pi>0,i=1∑Lpi=1
取灰度级为阈值将这幅图像的像素点分成 C 1 C_1 C1C_2和两簇,
- C 1 C_1 C1包含像素级为[1,2,…,t]的像素
- C 2 C_2 C2包含像素级为[t+1,…,L]的像素
对于图像中某个像素属于 C 1 / C 2 C_1/C_2 C1/C2类的概率可表示为:
ω 1 ( t ) = ∑ i = 1 t p i \omega_{1}(t)=\sum_{i=1}^{t}p_{i} ω1(t)=i=1∑tpi
ω 2 ( t ) = ∑ i = t + 1 L p i \omega_{2}(t)=\sum_{i=t+1}^{L}p_{i} ω2(t)=i=t+1∑Lpi
w 1 ( t ) , w 2 ( t ) w_1(t),w_2(t) w1(t),w2(t),满足关系 w 1 ( t ) = 1 − w 2 ( t ) w_1(t) = 1-w_2(t) w1(t)=1−w2(t)
求每个簇对应的像素均值:
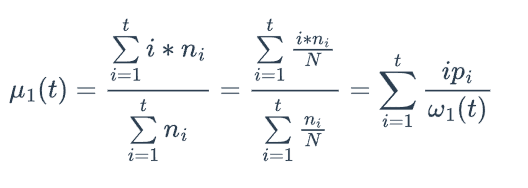
同样可推导:
μ 2 ( t ) = ∑ i = t + 1 L i p i ω 2 ( t ) \mu_{2}(t)=\sum_{i=t+1}^{L}\frac{i p_{i}}{\omega_{2}(t)} μ2(t)=i=t+1∑Lω2(t)ipi
整幅图像的像素均值记为:
μ T = ∑ i L i ∗ p i = ω 1 ( t ) μ 1 ( t ) + ω 2 ( t ) μ 2 ( t ) \mu_{T}=\sum_{i}^{L}i*p_{i}=\omega_{1}(t)\mu_{1}(t)+\omega_{2}(t)\mu_{2}(t) μT=i∑Li∗pi=ω1(t)μ1(t)+ω2(t)μ2(t)
求 C 1 / C 2 C_1/C_2 C1/C2每个簇对应的像素值方差:
σ 1 2 ( t ) = ∑ i = 1 t [ i − μ 1 ( t ) ] 2 ∗ n i ∑ i = 1 t n i = ∑ i = 1 t [ i − μ 1 ( t ) ] 2 ∗ n i N ∑ i = 1 t n i = ∑ i = 1 t [ i − μ 1 ( t ) ] 2 p i ω 1 ( t ) \sigma_{1}^{2}(t)=\frac{\sum_{i=1}^{t}[i-\mu_{1}(t)]^{2}*n_{i}}{\sum_{i=1}^{t}n_{i}}=\frac{\sum_{i=1}^{t}\frac{[i-\mu_{1}(t)]^{2}*n_{i}}{N}}{\sum_{i=1}^{t}n_{i}}=\frac{\sum_{i=1}^{t}[i-\mu_{1}(t)]^{2}p_{i}}{\omega_{1}(t)} σ12(t)=∑i=1tni∑i=1t[i−μ1(t)]2∗ni=∑i=1tni∑i=1tN[i−μ1(t)]2∗ni=ω1(t)∑i=1t[i−μ1(t)]2pi
同样可推导:
σ 2 2 ( t ) = ∑ i = t + 1 L [ i − μ 2 ( t ) ] 2 p i ω 2 ( t ) \sigma_{2}^{2}(t)=\frac{\sum_{i=t+1}^{L}[i-\mu_{2}(t)]^{2}p_{i}}{\omega_{2}(t)} σ22(t)=ω2(t)∑i=t+1L[i−μ2(t)]2pi
为了衡量所取阈值的二值化效果,作者定义了三种方差,分别是:
类内方差:
σ W 2 = ω 1 σ 1 2 + ω 2 σ 2 2 \sigma_{W}^{2}=\omega_{1}\sigma_{1}^{2}+\omega_{2}\sigma_{2}^{2} σW2=ω1σ12+ω2σ22
类间方差:
σ B 2 = ω 1 ( μ 1 − μ T ) 2 + ω 2 ( μ 2 − μ T ) 2 = ω 1 ω 2 ( μ 1 − μ 2 ) 2 \sigma_{B}^{2}=\omega_{1}(\mu_{1}-\mu_{T})^{2}+\omega_{2}(\mu_{2}-\mu_{T})^{2}=\omega_{1}\omega_{2}(\mu_{1}-\mu_{2})^{2} σB2=ω1(μ1−μT)2+ω2(μ2−μT)2=ω1ω2(μ1−μ2)2
图像总的像素值方差:
σ T 2 = ∑ i = 1 L ( i − μ T ) 2 p i \sigma_{T}^{2}=\sum_{i=1}^{L}(i-\mu_{T})^{2}p_{i} σT2=i=1∑L(i−μT)2pi
可以推导三者之间有如下关系:
σ W 2 + σ B 2 = σ T 2 \sigma_{W}^{2}+\sigma_{B}^{2}=\sigma_{T}^{2} σW2+σB2=σT2
从上面的定义可以发现 σ W 2 / σ B 2 \sigma_{W}^{2}/\sigma_{B}^{2} σW2/σB2,于阈值t有关,而 σ T 2 \sigma_{T}^{2} σT2与阈值无关。
上面是的二阶函数,是的一阶函数,更易优化。最后,求阈值可以变成最大化类间方差
σ B 2 ( t ∗ ) = max 1 ≤ t ≤ L σ B 2 ( t ) \sigma_{B}^{2}(t^{*})=\operatorname*{max}_{1\le t\le L}\sigma_{B}^{2}(t) σB2(t∗)=1≤t≤LmaxσB2(t)
C++ 源码实现
// Include Libraries
#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/imgproc.hpp>using namespace std;
using namespace cv;int main() {// Read the image in grayscale formatMat testImage = imread("boat.jpg", IMREAD_GRAYSCALE);int bins_num = 256;// Get the histogramlong double histogram[256];// Initialize all intensity values to 0for (int i = 0; i < bins_num; i++) {histogram[i] = 0;}// Calculate the number of pixels for each intensity valuefor (int y = 0; y < testImage.rows; y++) {for (int x = 0; x < testImage.cols; x++) {histogram[(int)testImage.at<uchar>(y, x)]++;}}// Calculate bin edges and bin midslong double bin_edges[256];bin_edges[0] = 0.0;long double increment = 0.99609375;for (int i = 1; i < bins_num; i++) {bin_edges[i] = bin_edges[i - 1] + increment;}long double bin_mids[256];for (int i = 0; i < bins_num; i++) {bin_mids[i] = (bin_edges[i] + bin_edges[i + 1]) / 2;}// Calculate weights for each classlong double weight1[256];weight1[0] = histogram[0];for (int i = 1; i < bins_num; i++) {weight1[i] = histogram[i] + weight1[i - 1];}int total_sum = 0;for (int i = 0; i < bins_num; i++) {total_sum += histogram[i];}long double weight2[256];weight2[0] = total_sum;for (int i = 1; i < bins_num; i++) {weight2[i] = weight2[i - 1] - histogram[i - 1];}// Calculate class meanslong double histogram_bin_mids[256];for (int i = 0; i < bins_num; i++) {histogram_bin_mids[i] = histogram[i] * bin_mids[i];}long double cumsum_mean1[256];cumsum_mean1[0] = histogram_bin_mids[0];for (int i = 1; i < bins_num; i++) {cumsum_mean1[i] = cumsum_mean1[i - 1] + histogram_bin_mids[i];}long double cumsum_mean2[256];cumsum_mean2[0] = histogram_bin_mids[255];for (int i = 1, j = bins_num - 1; i < bins_num; i++, j--) {cumsum_mean2[i] = cumsum_mean2[i - 1] + histogram_bin_mids[j];}long double mean1[256];for (int i = 0; i < bins_num; i++) {mean1[i] = cumsum_mean1[i] / weight1[i];}long double mean2[256];for (int i = 0, j = bins_num - 1; i < bins_num; i++, j--) {mean2[j] = cumsum_mean2[i] / weight2[j];}// Calculate Inter_class_variancelong double Inter_class_variance[255];long double dnum = 10000000000.0; // Scaling factor to avoid overflowfor (int i = 0; i < 255; i++) {Inter_class_variance[i] = ((weight1[i] * weight2[i] * (mean1[i] - mean2[i + 1])) / dnum) * (mean1[i] - mean2[i + 1]);}// Maximize interclass variance to find the thresholdlong double maxi = 0;int getmax = 0;for (int i = 0; i < 255; i++) {if (maxi < Inter_class_variance[i]) {maxi = Inter_class_variance[i];getmax = i;}}cout << "Otsu's algorithm implementation thresholding result: " << bin_mids[getmax] << endl;return 0;
}
Python 代码实现
import cv2
import numpy as npdef otsu_thresholding(image_path):# 读取图像image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)if image is None:print("Error: 图像未找到.")return# 获取直方图hist = cv2.calcHist([image], [0], None, [256], [0, 256])# 计算总像素total_pixels = image.size# 初始化类间方差inter_class_variance = 0# 初始化权重和w0 = w1 = 0# 初始化类内总和sum0 = np.sum(image[image < inter_class_variance])sum1 = np.sum(image[image > inter_class_variance])# 初始化类内平方和var0 = np.sum((image[image < inter_class_variance] - sum0 / w0) ** 2)var1 = np.sum((image[image > inter_class_variance] - sum1 / w1) ** 2)# 寻找最佳阈值max_variance = 0threshold = 0for threshold in range(1, 256):w0 += hist[threshold - 1]w1 = total_pixels - w0sum0 += threshold * hist[threshold - 1]sum1 -= threshold * hist[threshold - 1]var0 = w0 / (w0 + w1) * np.sum((image[image <= threshold] - (sum0 / w0)) ** 2)var1 = w1 / (w0 + w1) * np.sum((image[image > threshold] - (sum1 / w1)) ** 2)inter_class_variance = var0 + var1if inter_class_variance > max_variance:max_variance = inter_class_variancethreshold = threshold# 使用最佳阈值二值化图像_, binary_image = cv2.threshold(image, threshold, 255, cv2.THRESH_BINARY)return binary_image, threshold# 使用函数
image_path = 'boat.jpg' # 请确保路径正确
binary_image, threshold = otsu_thresholding(image_path)# 显示结果
cv2.imshow('Original Image', cv2.imread(image_path, cv2.IMREAD_GRAYSCALE))
cv2.imshow('Binary Image', binary_image)
cv2.waitKey(0)
cv2.destroyAllWindows()