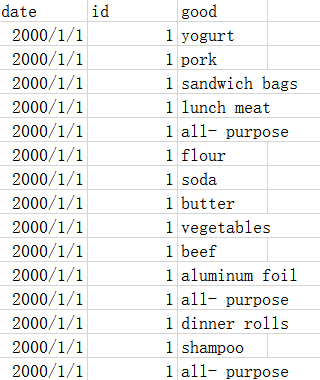🚀 【考纲要求】图的基本概念
一、图的基本概念
1.1 图的定义
图由顶点和边组成,所以我们在表示一个图的时候,使用 G = ( V , E ) G=(V,E) G=(V,E),来表示一个G图,其中的V表示G图中的顶点,E表示G图中的边;对于G图中顶点和边的表示就是采用集合的形式来表示, V = { v 1 , v 2 , v 3 ⋅ ⋅ ⋅ ⋅ } V= \{v_{1},v_{2},v_{3}···· \} V={v1,v2,v3⋅⋅⋅⋅},同样的对于边E也可以采用集合来表示出来;同时图的顶点集不可以为空,图的边集可以为空,每一条线都要连接两个节点。
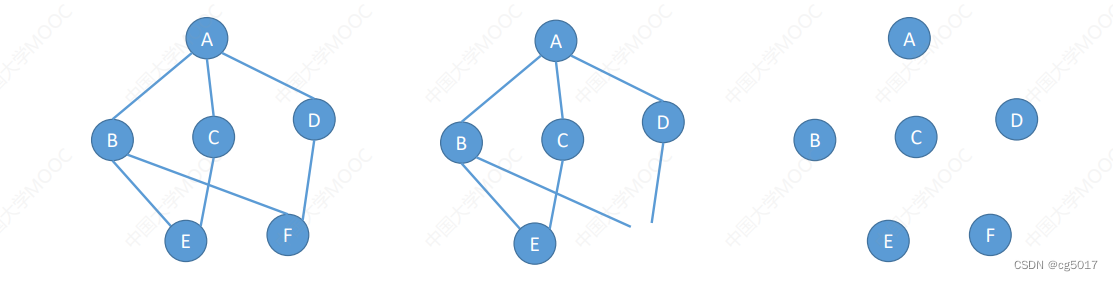
所以根据图的定义可知,上述中第二个就不可以为图,因为B和D的两条线有没有连接上点的,最后一个也是图,顶点集不为空,边集为空,可以称之为图。
1.2有向图、无向图、带权图、简单图、多重图
①定义
有向图: 其实描述的是图中顶点和顶点的连线是有方向的连接,如下图所示,AB两个点之间的连接都是有方向的连接。
边的集合 <A,B>表示的是A可以到B,与 <B,A>是不同的,这个表示的是B可以到A。

无向图: 其实描述的是图中顶点和顶点的连线是没有方向的连接。
边的集合中(A,B)表示A可以到B,B也可以到A,与(B,A)是相同的。

②顶点的度、入度、出度
在学习入度和出度之前,我们先来看个实际的例子,对于微信好友、微博粉丝关系的存储就是使用图这种数据结构来存储的,但是对于微信好友来说,应该是使用无向图来存储的,因为一旦好友建立了,那么两个人就可以互相的通信;而对于微博粉丝的关系来说,因该使用有向图来存储,因为关注对方成为对方的粉丝是单项的;那马现在我们知道哪个人是社交达人,哪个是微博大V的话,我们该如何统计呢?这就是入度和出度的具体意义了。
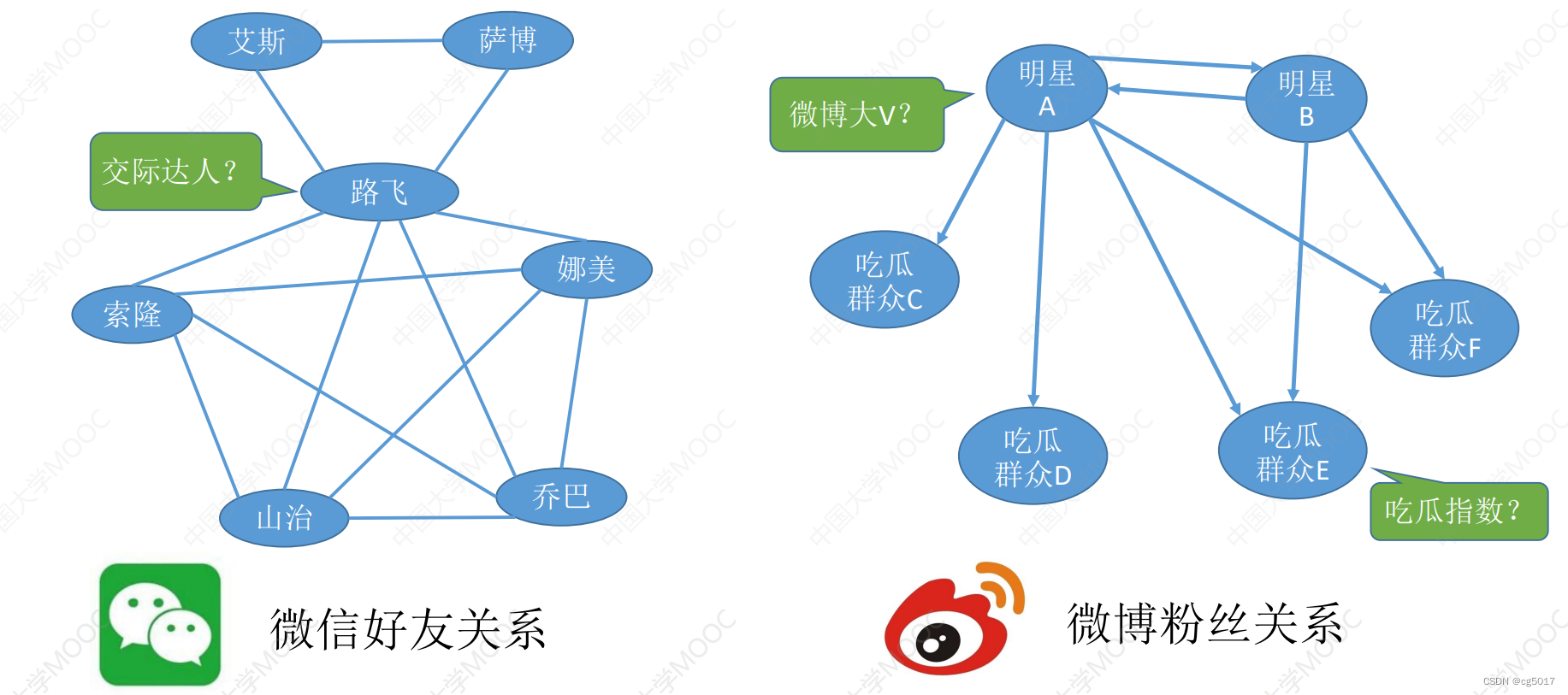
顶点的度: 对于明星A来说该节点的度就是6,到C一个,到D一个,到E一个,到F一个,到B一个,B到A一个,所以总共6个路径可以到达A要么从A出去,所以度为6;对于路飞来说,和他连着的有6个线,但是度为 6 ∗ 2 = 12 6*2=12 6∗2=12,因为是无向图,每一个连线既可以到达也可以出去。
入度和出度是正对于有向图来说的
入度: 进入该节点的度,对于明星A节点来说,该节点的入度是1,只有一个进入。
出度: 从该节点出去的有五个,所以该节点的出度就是5。
回到一开始的问题,入度和出度的有什么具体意义?想要知道哪个人是社交达人,只需统计每个节点的度数。想知道哪个是大V,只需统计每个节点的出度,即被关注量。
③带权图
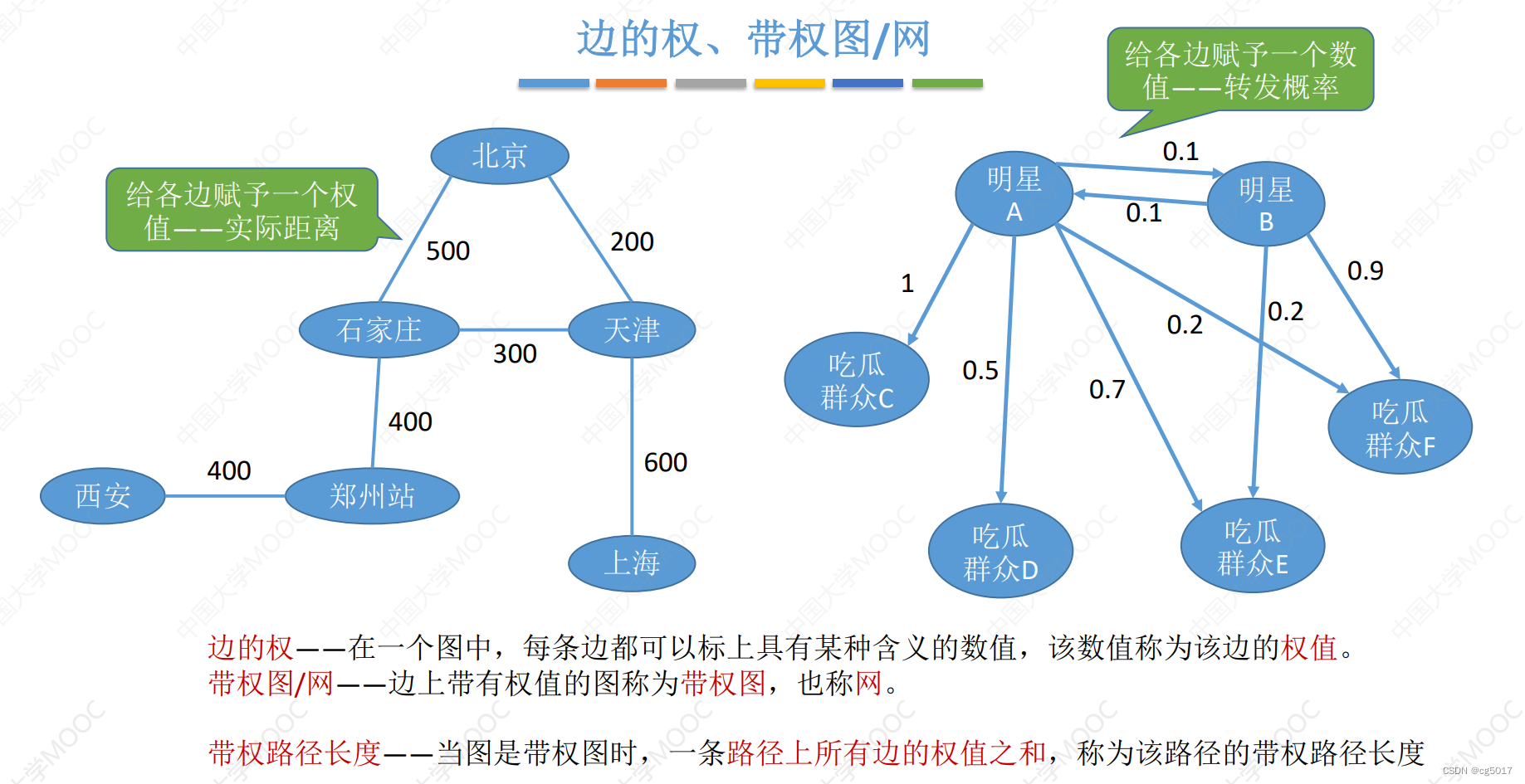
1.3点到点的关系
- 路径 从某一点到另外一点的路径是指由顶点组成的序列
- 回路 第一个顶点和最后一个顶点相同的路径称为回路或环
- 简单路径 路径序列中,点不重复
- 简单回路 回路中,点不重复
- 路径长度 经过的边的个数
- 点到点的距离 有路径则路径长度为其距离,若无路径则为 ∞ ∞ ∞
- 无向图的连通性、连通图 和 有向图的强连通性,强连通图
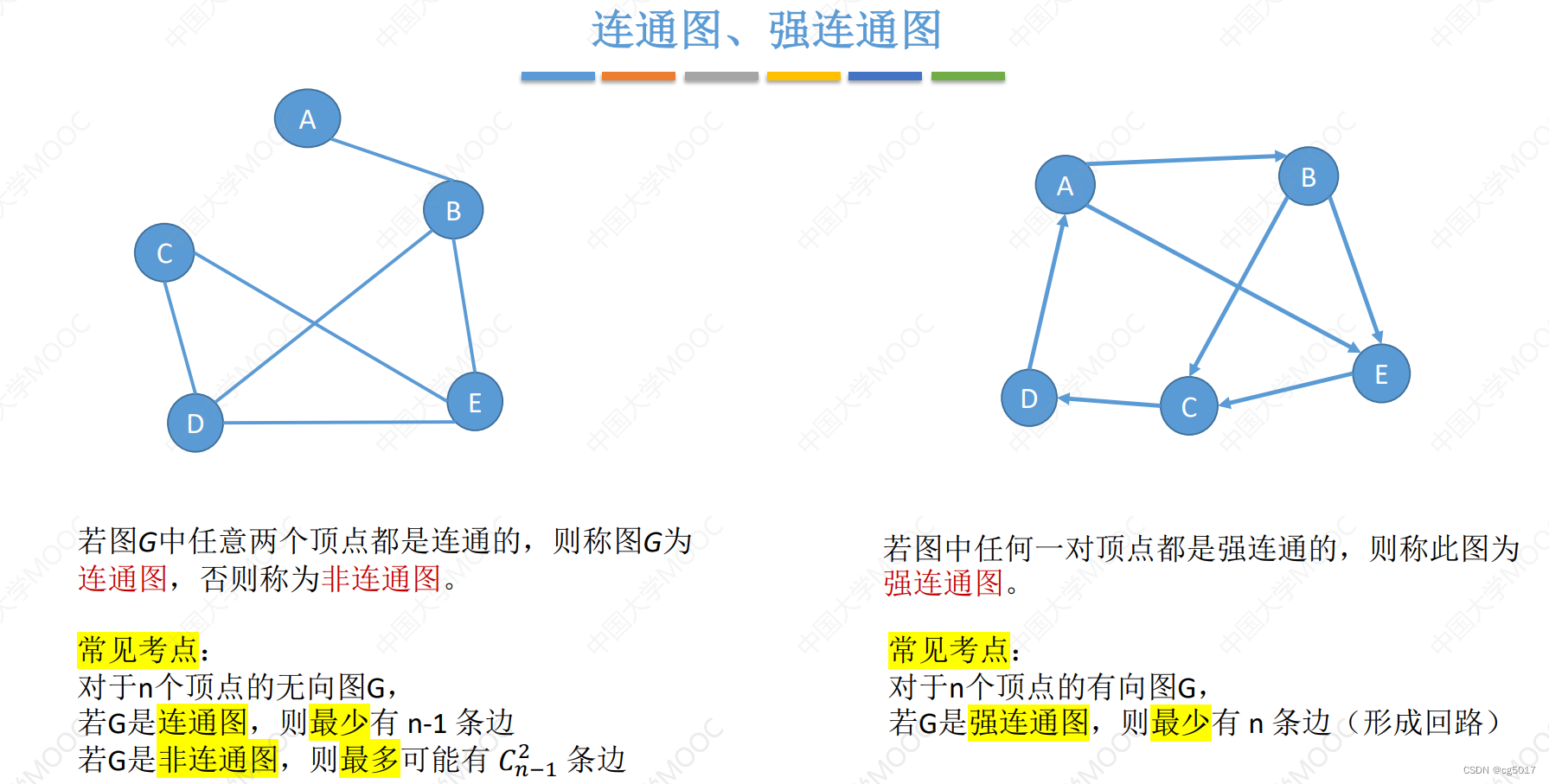
对于无向图来说,其连通性就是每个节点都有线连着,对于有向图来说,任意一个顶点可达任意一个顶点,就是具有强连通性。
1.4 图的局部
-
子图
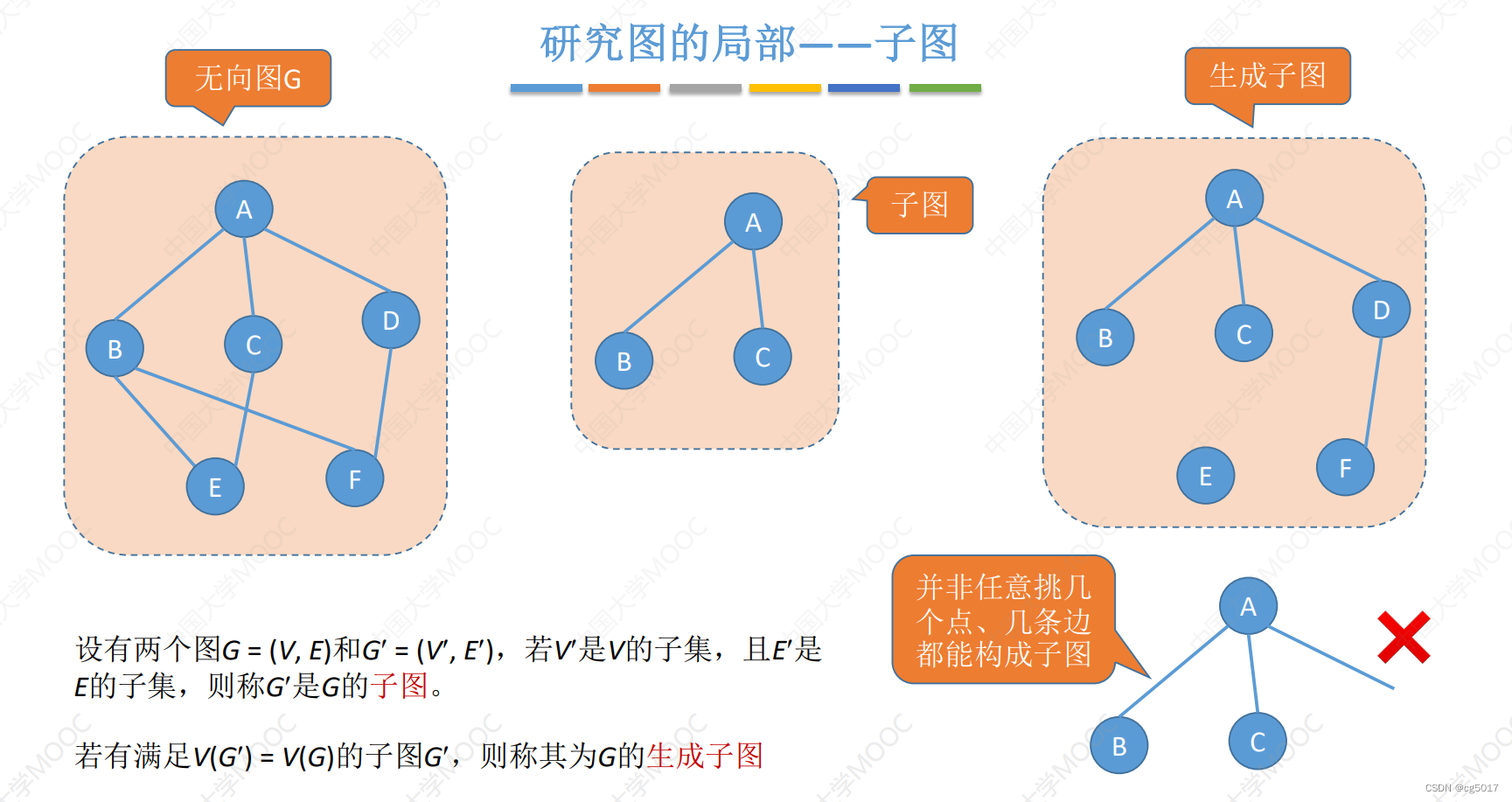
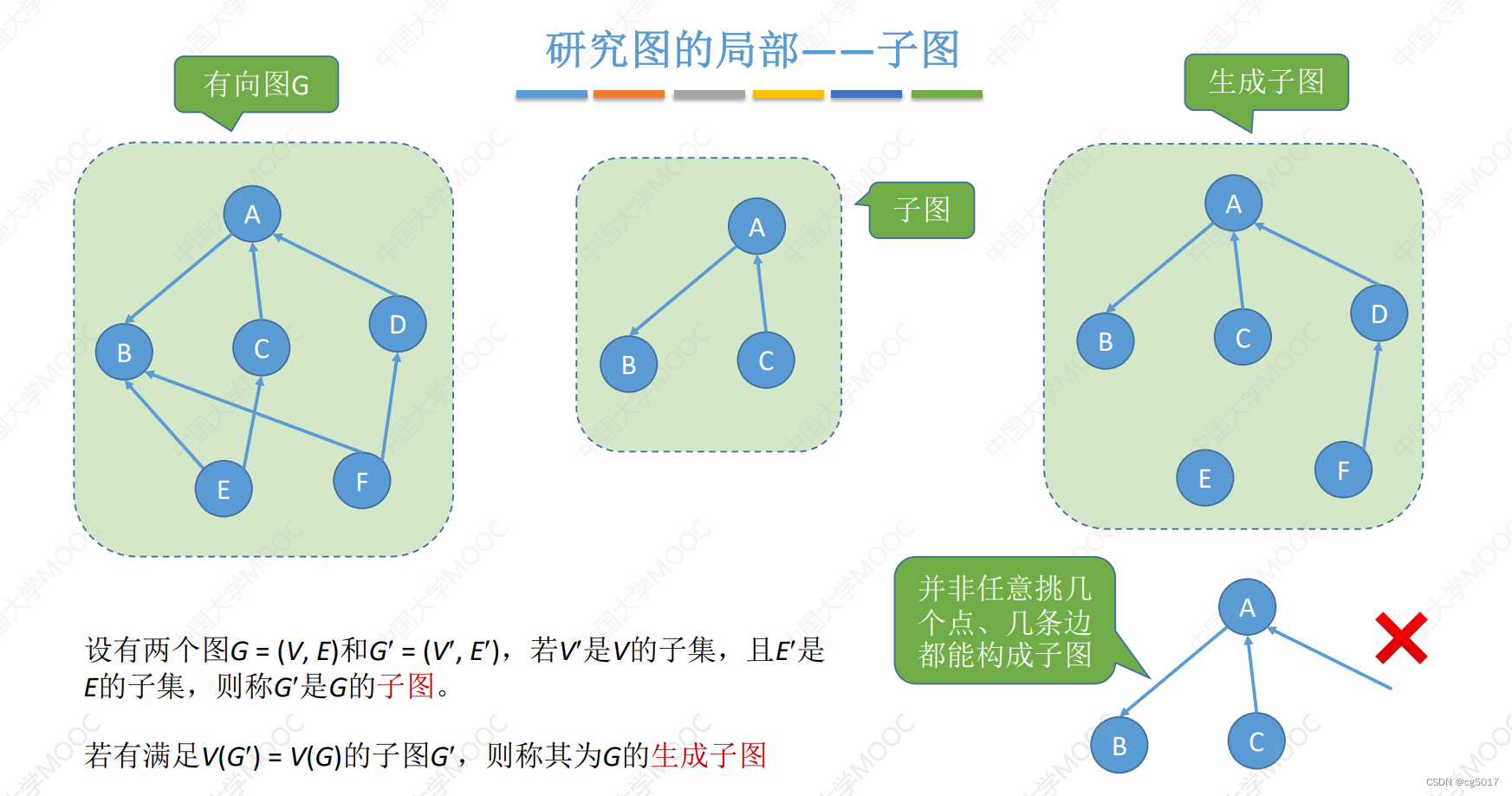
-
连通分量——极大连通子图
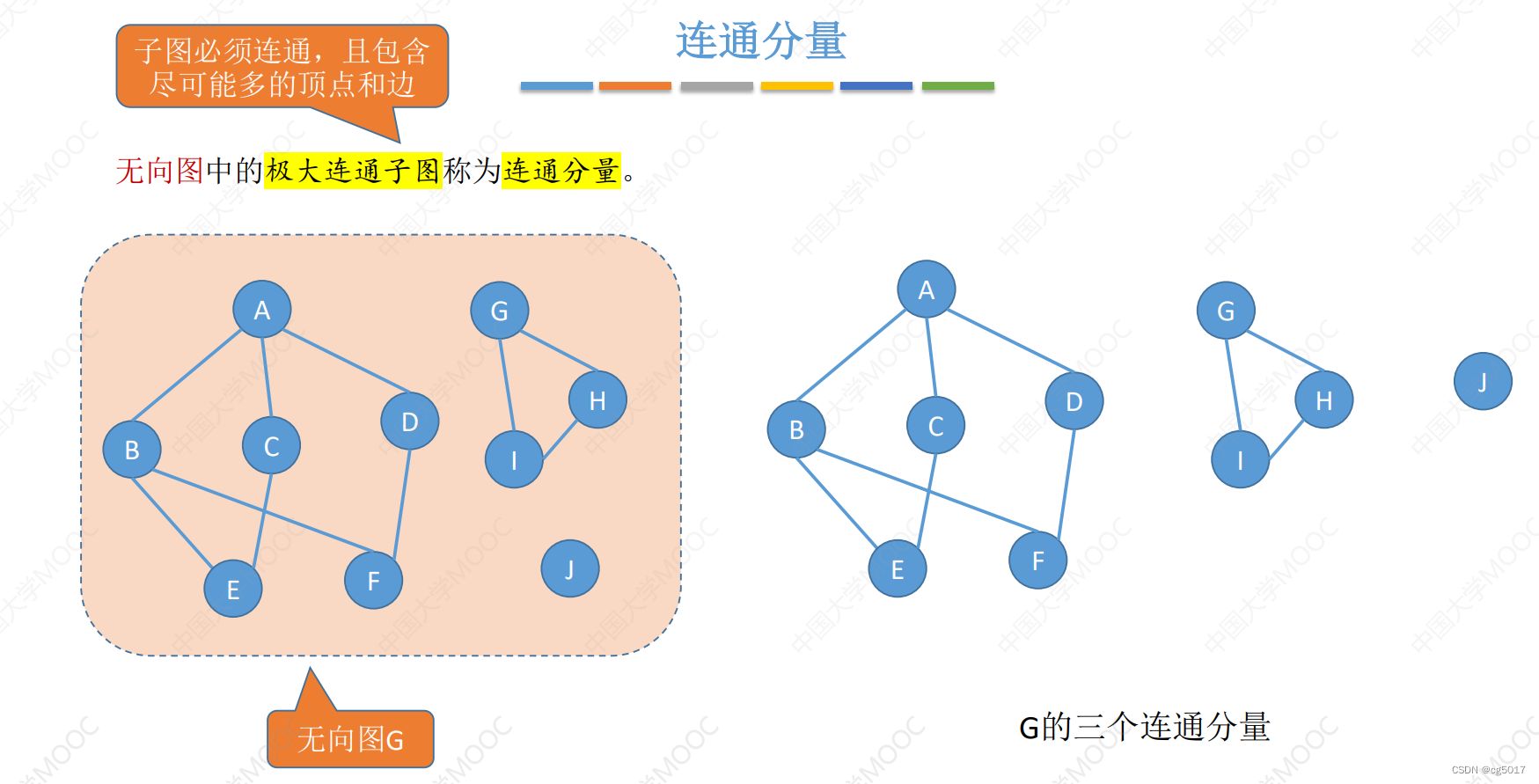
将连通分量称其为极大连通子图更好理解,所谓的极大的连通子图就是要尽可能的满足让子图是最大的连通图。 -
强连通分量——极大强连通子图
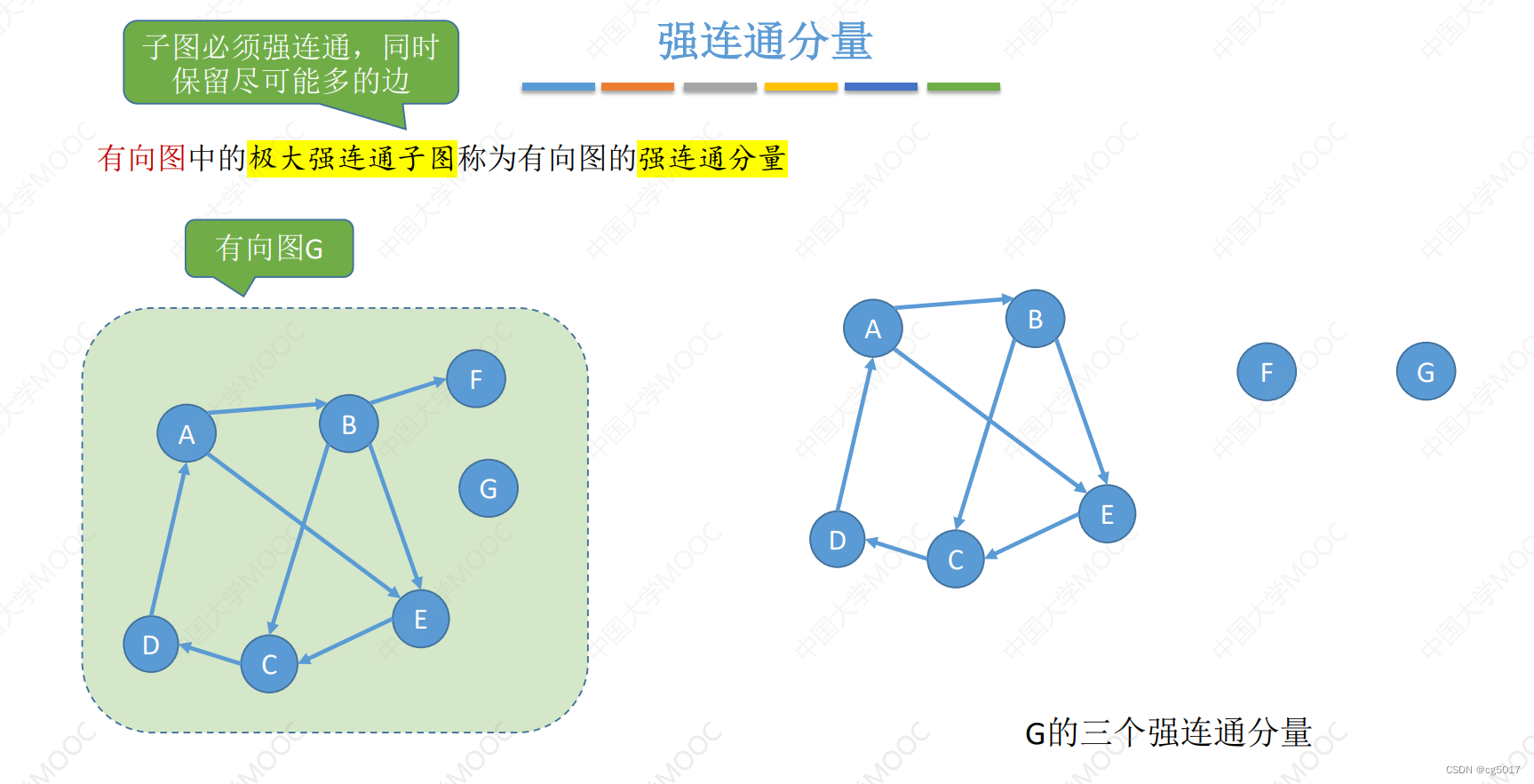
将强连通分量称其为极大强连通子图更好理解,所谓的极大的强连通子图就是要尽可能的满足让子图是最大的强连通图。 所以不能将节点F给划入子图,因为F的加入,F不能到达ABDCF,不为强连通图。
-
连通无向图的生成树
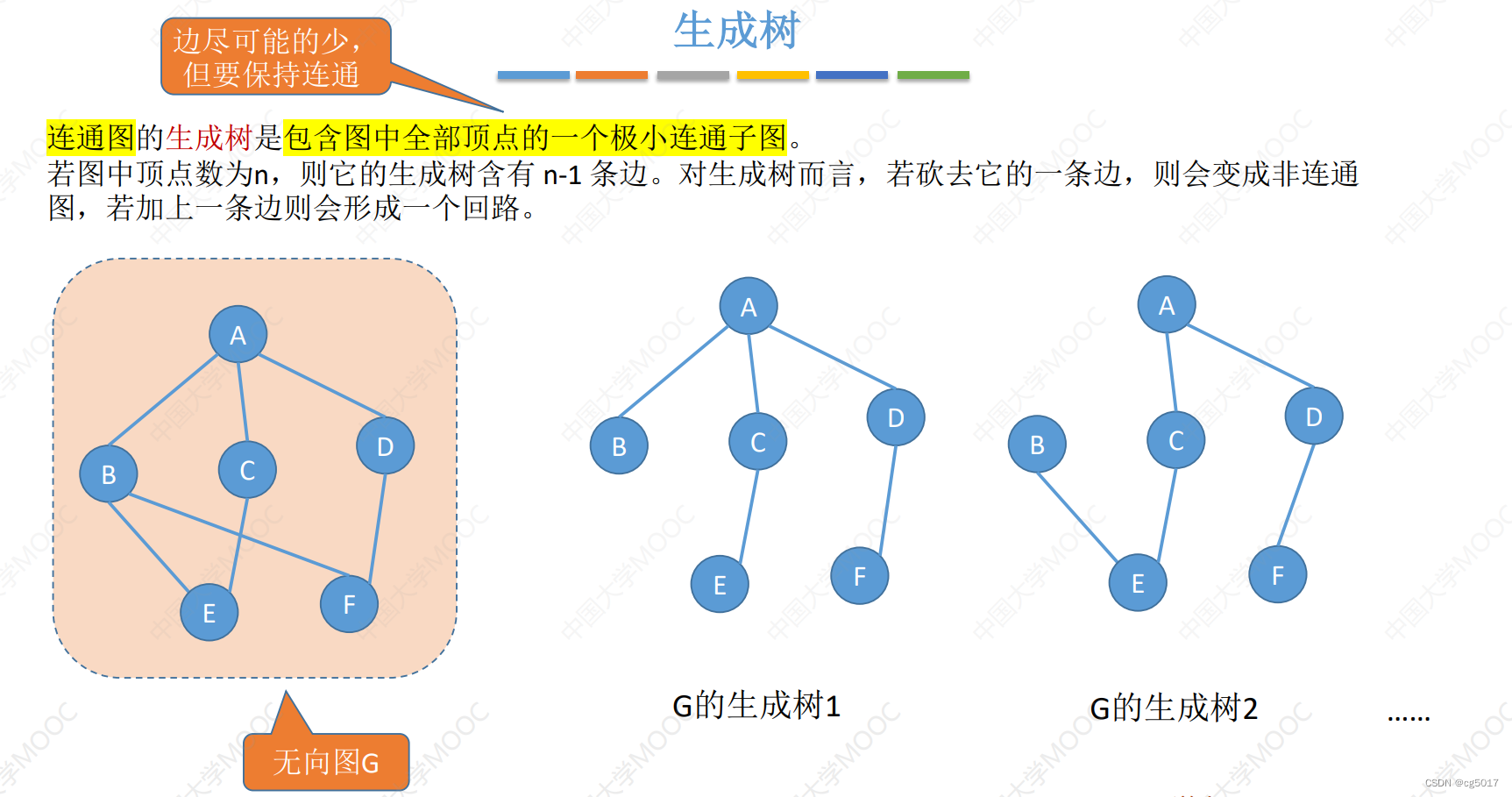
-
非连通无向图的生成森林
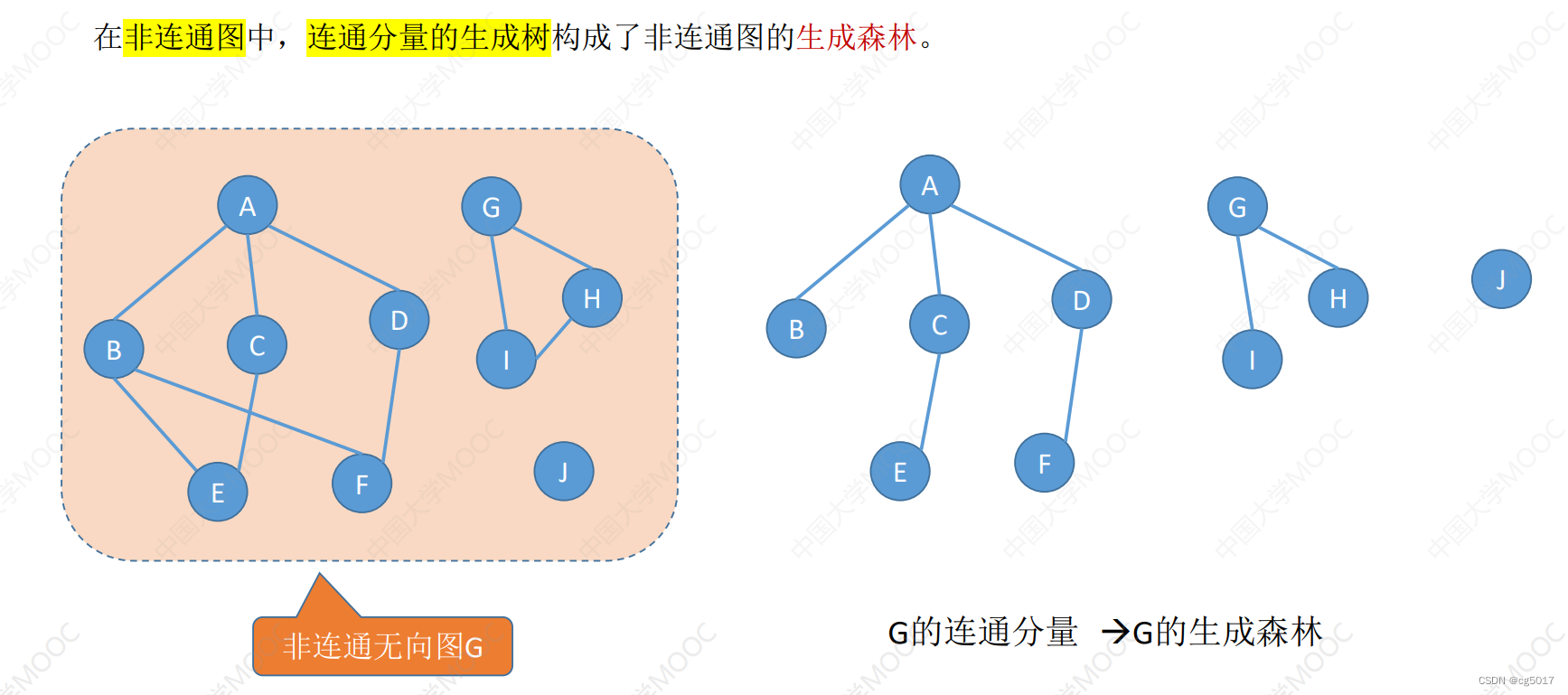
1.5 几种特殊形态的图
① 完全图
就是顶点之间全都互相连接
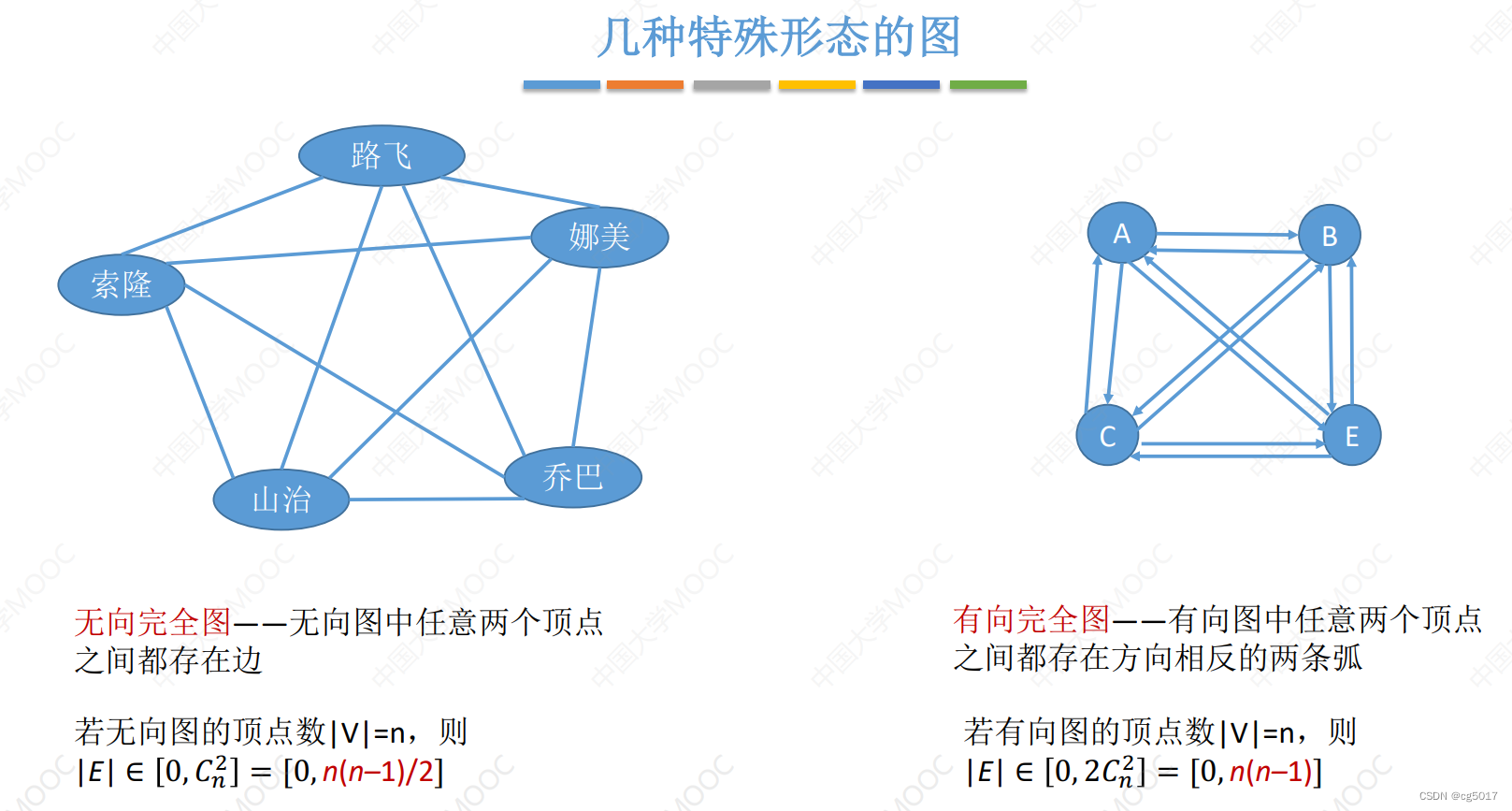
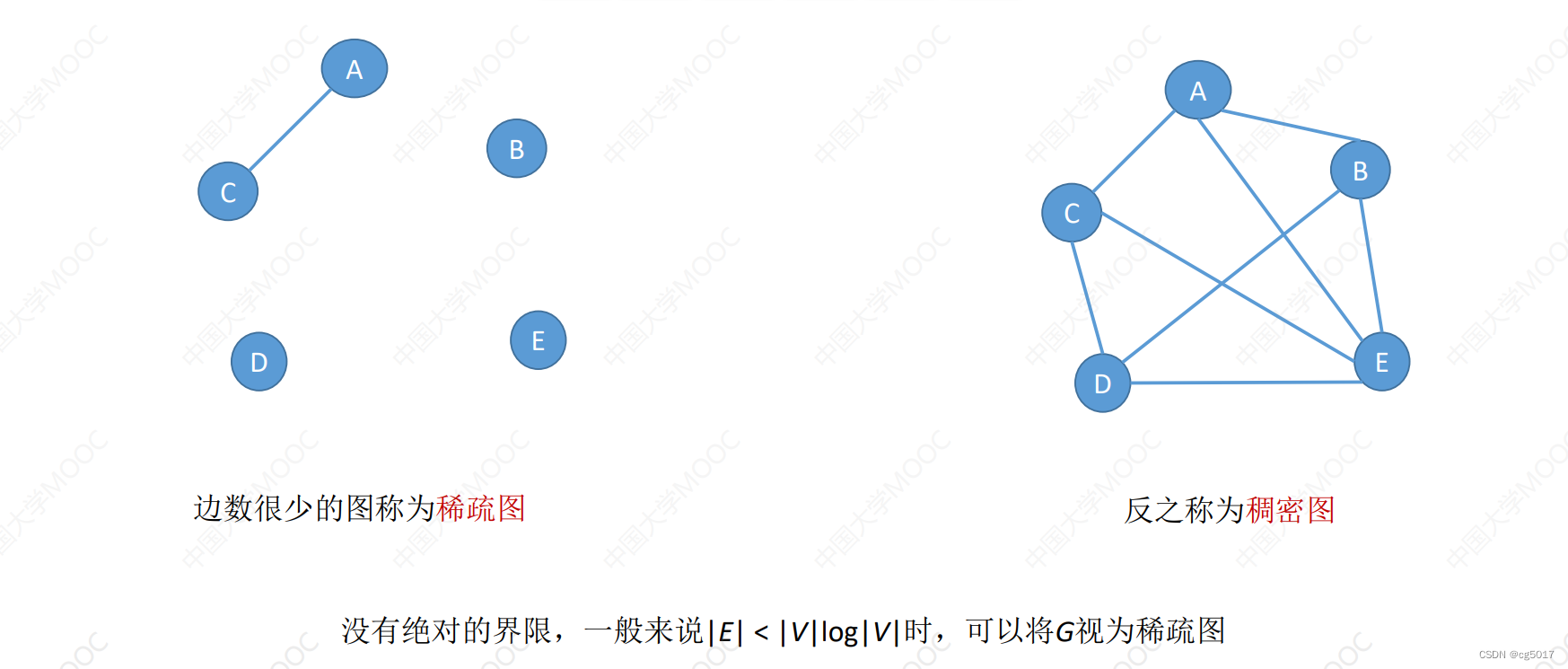
②稠密图、稀疏图
了解即可
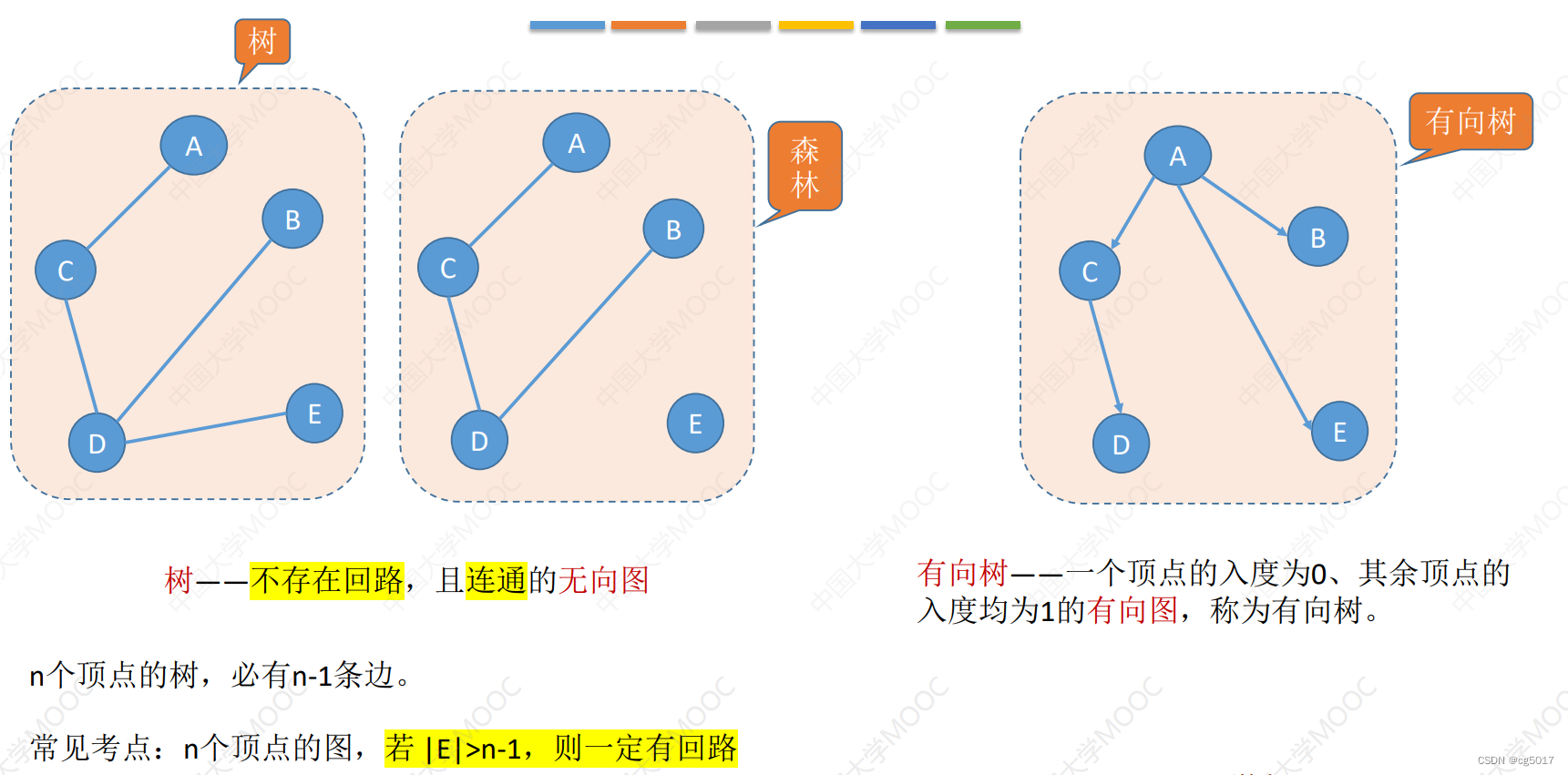
③树、森林、有向树
N个节点够成树是需要N-1个边,所有只有多有一个边,就会产生回路。