面试题 02.02. 返回倒数第 k 个节点 - 力扣(LeetCode)
思路1:先计算出链表的长度,在将链表中的值存在数组中,在返回第k个节点。
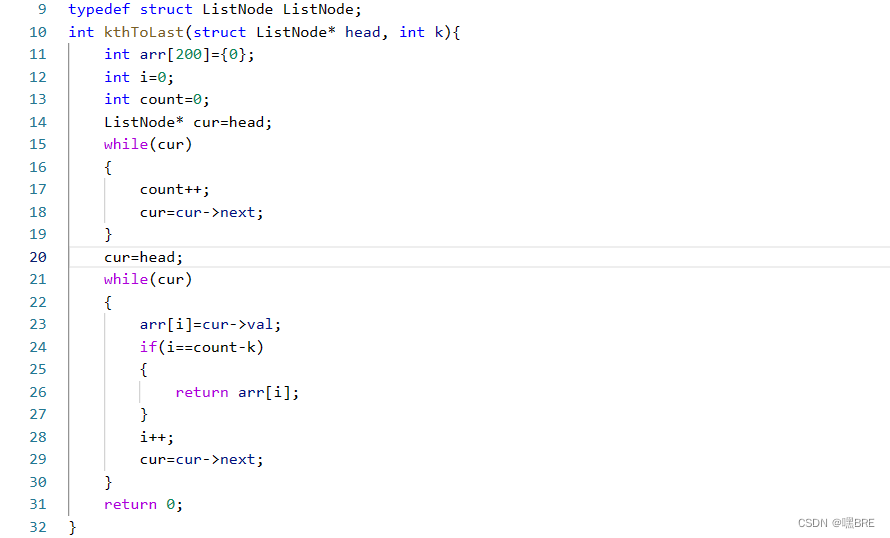
思路2:利用快慢指针,先让快指针走k步,在让快慢指针分别同时走,当快指针走到空的时候,慢指针就是倒数第k个节点。

链表的回文结构_牛客题霸_牛客网 (nowcoder.com)
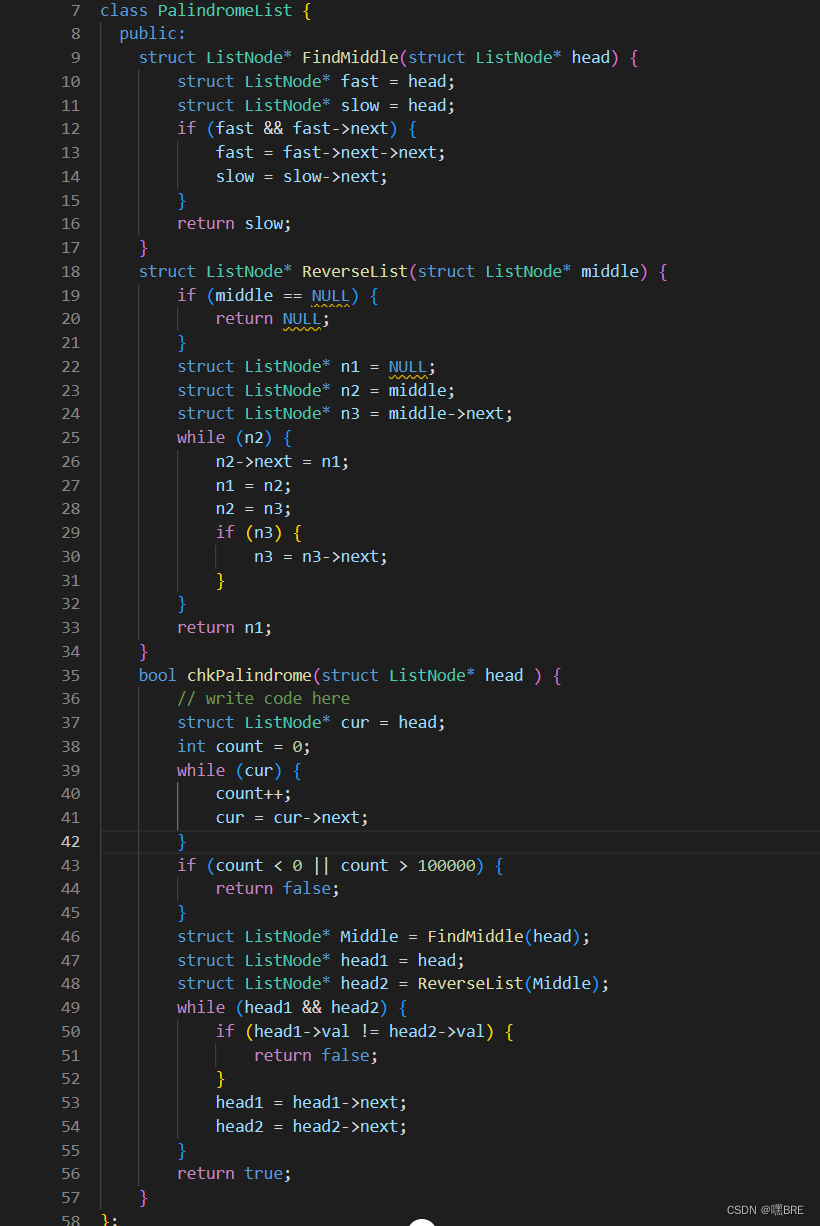
思路:先使用快慢指针找到来链表的中间节点,在将中间节点之后的链表倒置(注意倒置之后,中间链表的前一个节点依然指向尾结点),最后遍历链表,判断链表是否是回文结构。
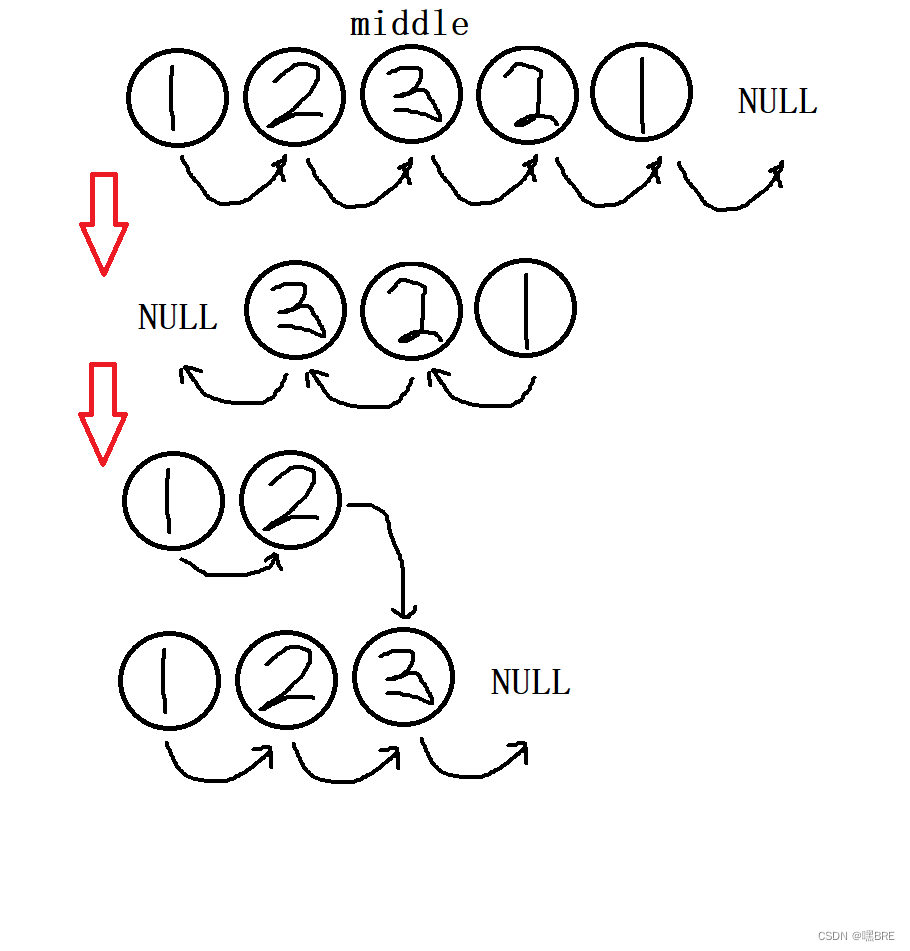
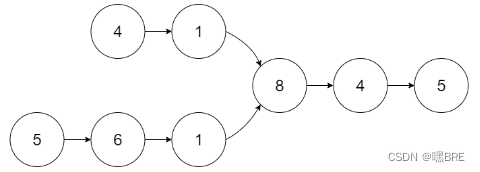
160. 相交链表 - 力扣(LeetCode)
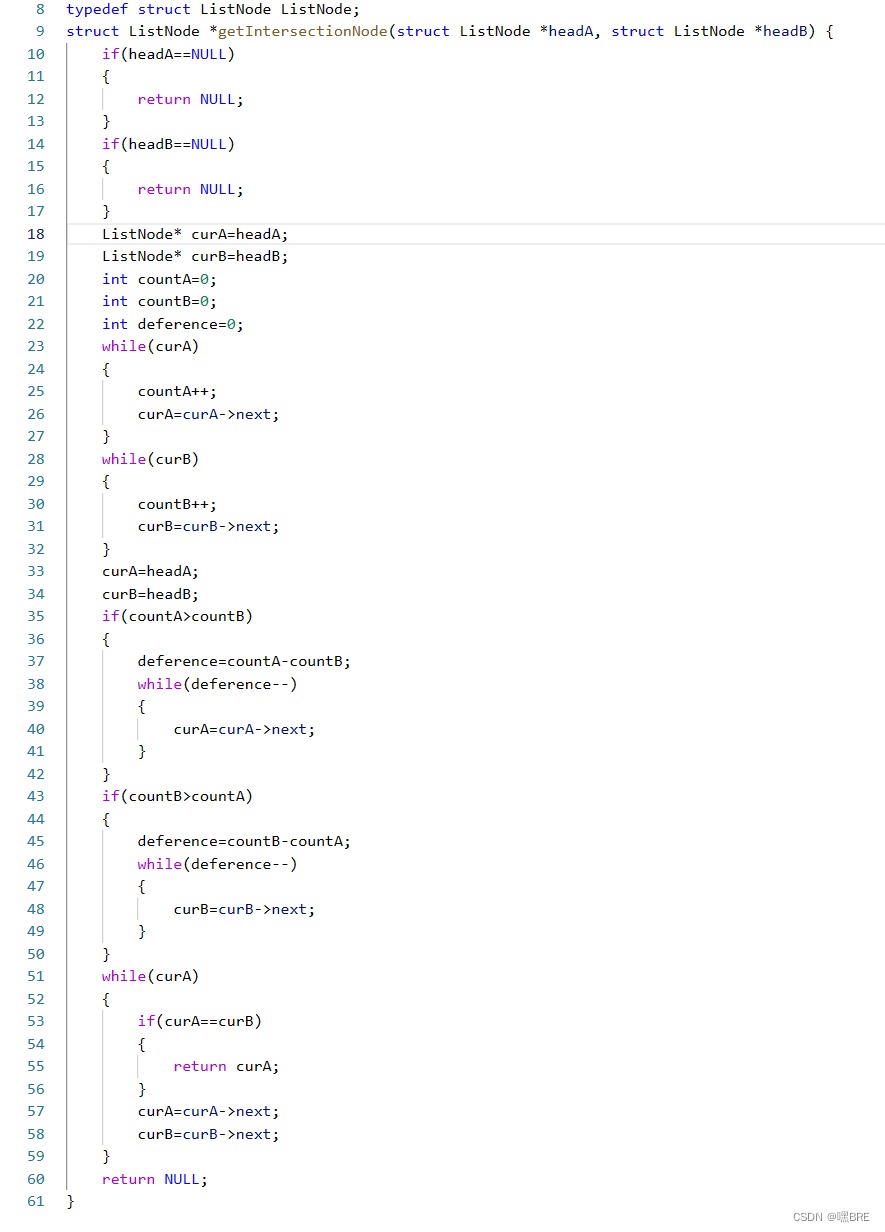
思路:先分别计算出两个链表的长度,算出它们长度之间的差值deference,再让长度较长的链表先走deference步,这样两个链表的长度就会相等,再进行遍历链表,找出相交点(注意,在寻找相交点的时候要找节点的地址,不能找节点的val值)。
141. 环形链表 - 力扣(LeetCode)
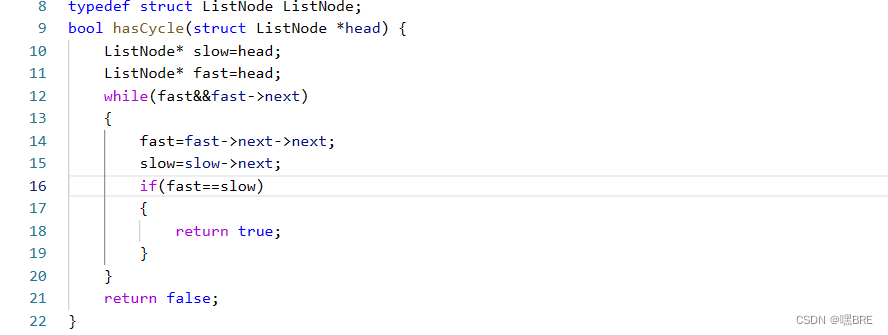
思路:使用快慢指针,如果fast或者fast->next为空的话说明链表不是一个环形链表,如果fast节点等于slow节点的话,说明fast追上了slow节点(fast一定会追上slow节点,这个结论会在下文解释到),也就说明了链表会进入一个环形的链表。
环形链表的几种情况:

那么,我们就要提出几个问题:
1.为什么一定会相遇,有没有可能错过,永远也追不上?
2.fast节点走3步,4步,或者n步是否可以与slow指针相遇?
先来解答第一个问题:

假设slow进入环的时候slow与fast节点的距离为N,fast节点每次走两步,slow节点每次走一步,所以每当slow节点走一步的时候,快慢指针之间的距离就会缩小1,直到它们之间的距离变为0.
slow走的步数 fast与slow之间的距离
0 N
1 N-1
2 N-2
…… ……
x 0
第二个问题:
我们先来观察slow节点每次走1步和fast节点每次走3步时候的情况
这时候,我们需要分两种情况来分析两个指针:
a.当slow节点进入环的时候,快慢指针之间的距离N是一个偶数
b.当slow节点进入环的时候,快慢指针之间的距离N是一个奇数
slow走的步数 快慢指针之间的距离(N为偶数) 快慢指针之间的距离(N为奇数)
0 N N
1 N-2 N-2
2 N-4 N-4
…… …… ……
x-1 2 1
x 0 -1
在这里,我们发现快慢指针之间的距离N是一个奇数时,fast与slow会错过,永远也不会相遇。
但是,先别急,这个结论真的正确吗?或者我们说快慢指针之间的距离N有可能是一个奇数吗?这就需要我们再次证明一下:
我们分析一下追上与追不上的情况:
1.N是偶数,第一轮就可以追上
2.N是奇数,第一轮追击就会错过,距离变成C-1
a.如果C-1是偶数,下一轮就追上了
b.如果C-1是奇数,那么就永远也追不上了
综上所述:同时存在N是奇数并且C是偶数,那么就永远也追不上了,我们接下来探讨的就是是否存在这种情况。
假设在slow节点进环时,slow节点走的长度为L ,fast节点走的距离为L+x*N+C-N, 整个环的长度为C。
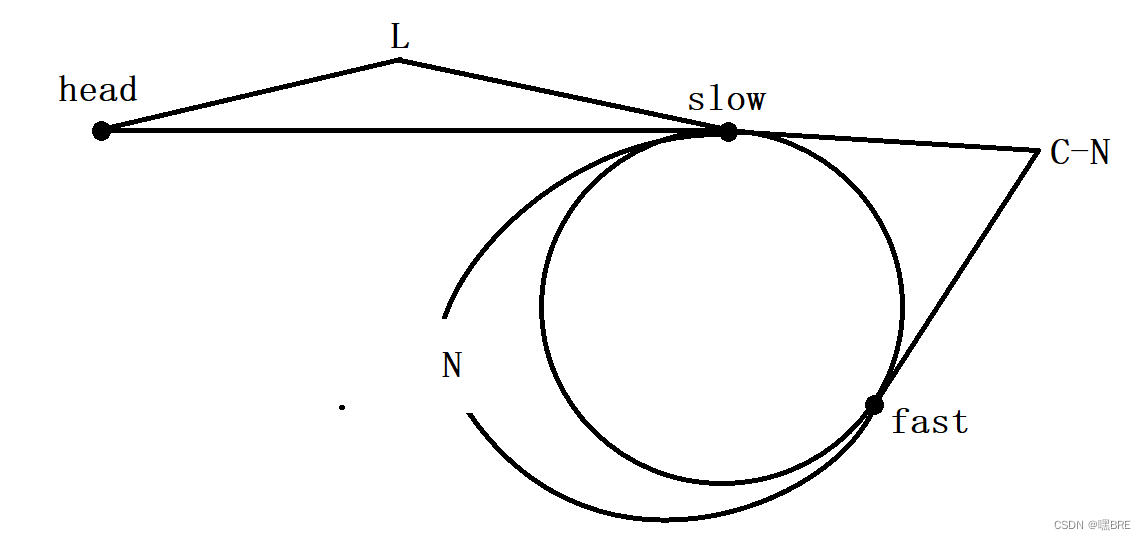
在slow节点进环时,fast与slow节点分别走过的距离为:
fast:L+x*N+C-N (x为快指针绕环走的圈数)
slow:L
接下来,因为fast节点走过的距离是slow节点走过的距离的3倍,所以我们会得到一个等式:
3*L=L+x*C+C-N
→2*L=x*C+C-N
→2*L=(x+1)*C-N
等式的左边一定是一个偶数,右边如果N是一个奇数,那么C一定也是一个奇数;右边如果是一个偶数,那么C一定也是一个偶数。所以就不会存在N是奇数并且C是偶数的情况。所以fast节点每次走3步的情况下,就不存在fast节点追不上slow节点的情况。
按这种方法证明其他fast节点走n步的情况,依然可以证明出fast节点一定可以追上slow节点的结论。
142. 环形链表 II - 力扣(LeetCode)

这道题目要求我们找到进入环形链表的节点,并且返回节点。
思路:首先找到快慢指针相遇的节点,此时,meet节点就是slow指针。meet指针到环形链表入口与head节点到环形链表的距离相等。
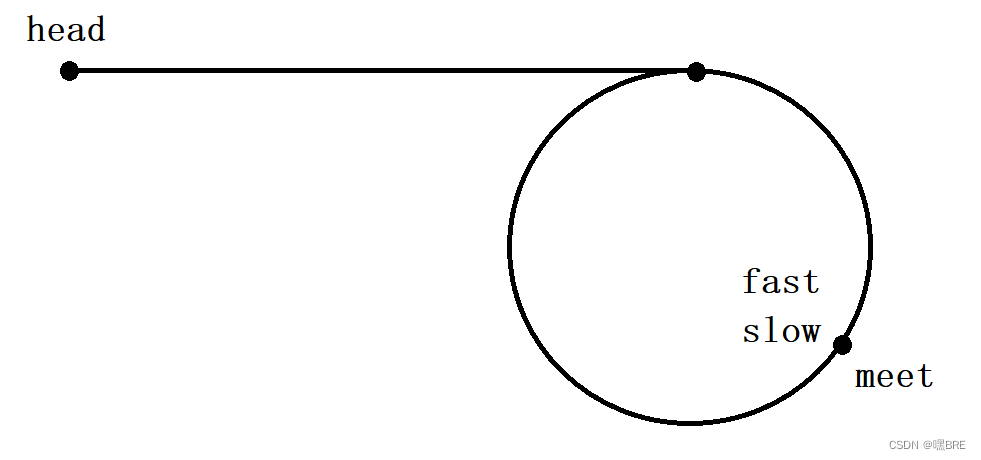
那么,为什么meet指针到环形链表入口与head节点到环形链表的距离相等呢?
证明:
我们假设head到入口的距离为L,入口到meet节点的距离为N,整个环的长度为C。
在相遇时,fast与slow节点分别走过的距离为:
fast:L+x*C+N (x为快指针绕环走的圈数)
slow:L+N(slow指针在没有走完第一圈的时候就会被追上,因为当slow节点进入环的时候,fast指针已经在环中走了一段时间,二fast节点的速度有是slow节点的两倍,所以slow节点会在走完一圈之前就被fast节点追上)
接下来,因为fast节点走过的距离是slow节点走过的距离的两倍,所以我们会得到一个等式:
2*fast=slow
→2*L+2*N=L+x*C+N
→ L+N=x*C
→ L=x*C-N
→ L=(x-1)*C+C-N
到这里我们会发现C-N的距离其实就是meet节点到环入口的距离,这个距离加上若干个环的长度就是L的长度。所以让meet节点和head节点分别同时走,它们一定会在环的入口处相遇。
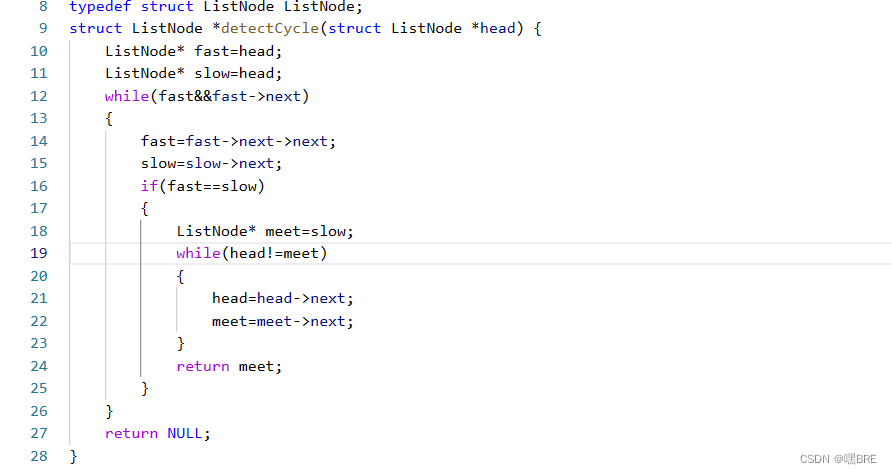
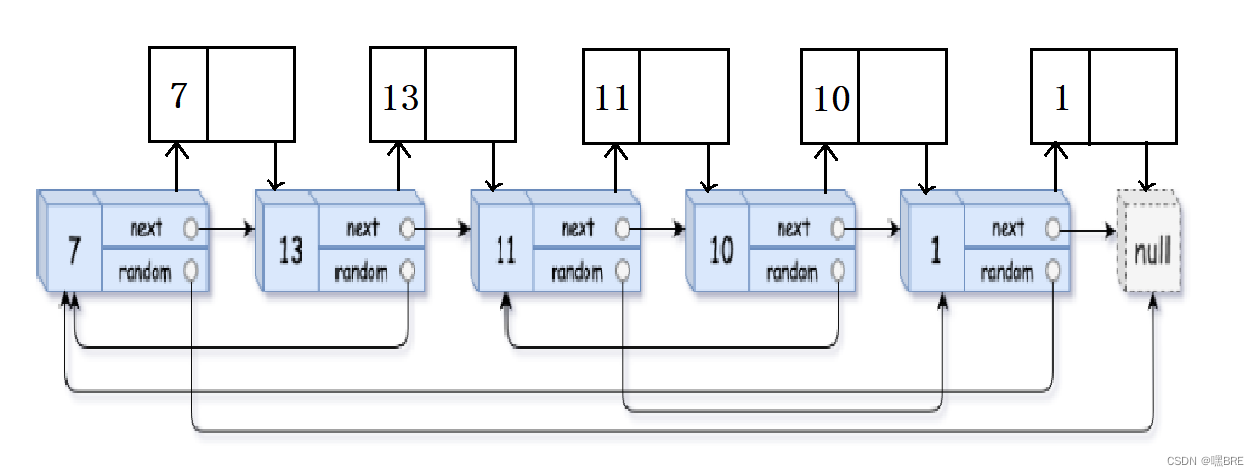
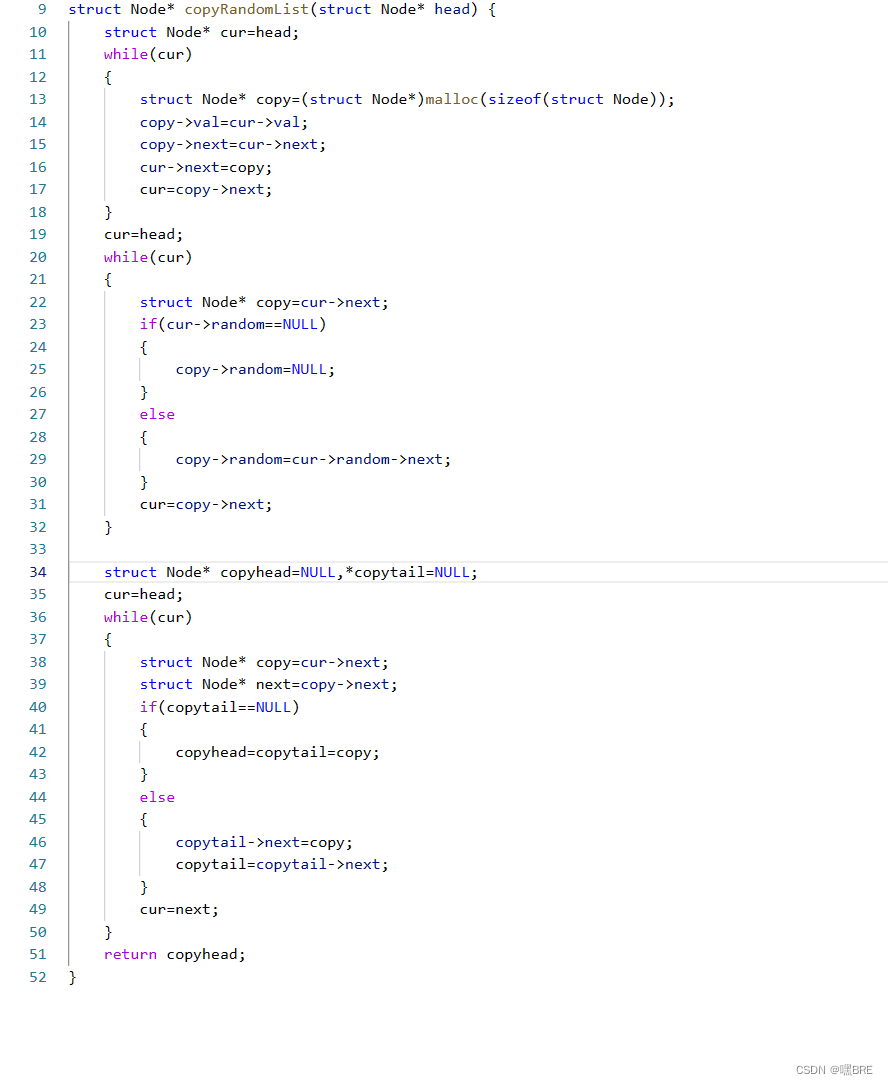
138. 随机链表的复制 - 力扣(LeetCode)
思路:在每个节点之后创建一个节点并将节点的值赋给创建的节点,再将random指向cur->random->next。最后将创建出的链表尾插到一个新的链表中。