文章目录
- 题目
- 二叉树
- 二叉树描述
- 二叉树的java描述和前序遍历、后序遍历、中序遍历
- 题解
- 总结以及二叉树应用场景
题目
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
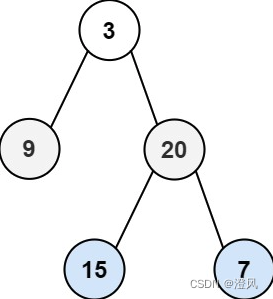
输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:输入:root = [1]
输出:[[1]]
示例 3:输入:root = []
输出:[]
提示:树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) {this.val = val;}TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}
二叉树
二叉树描述
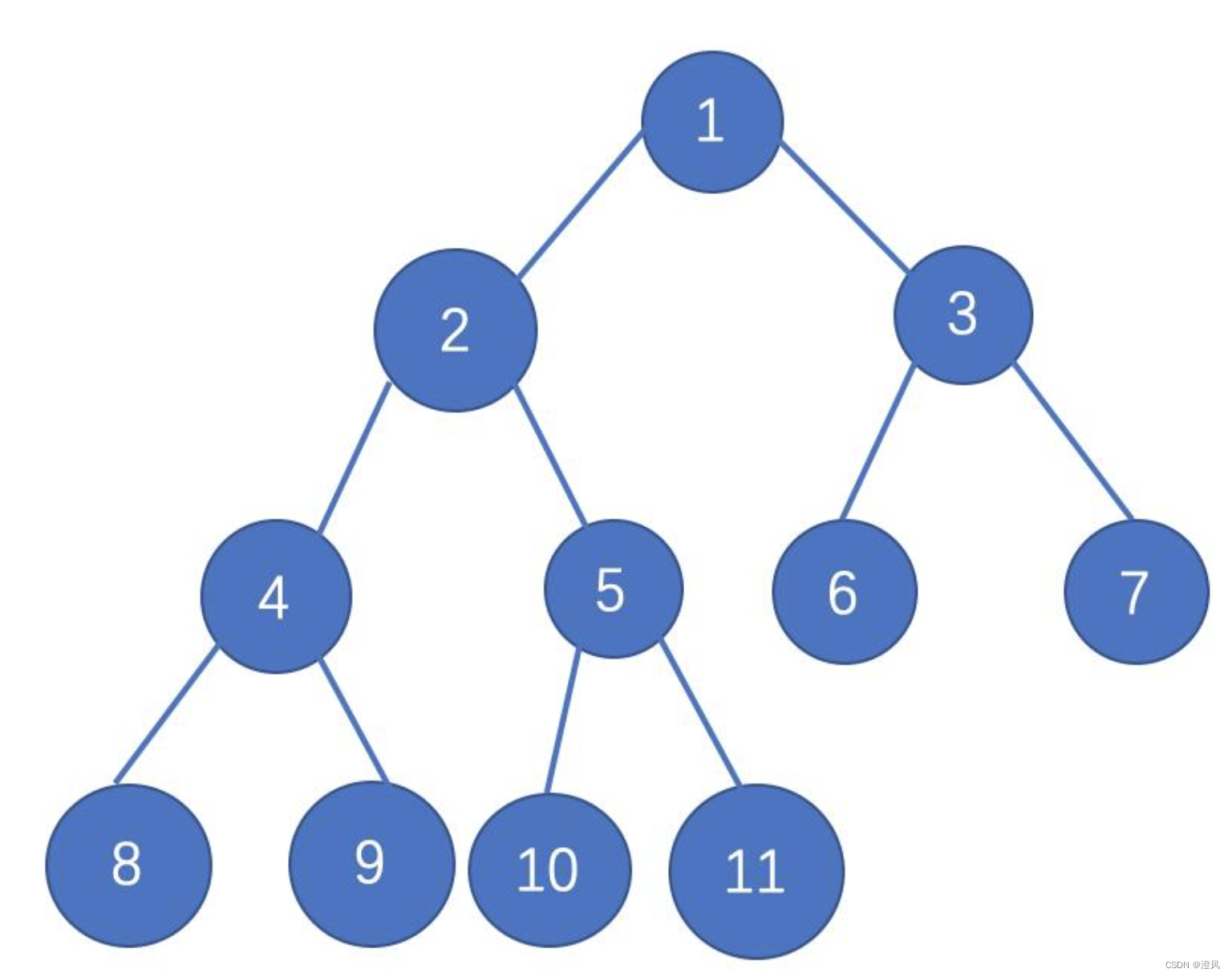
二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的特点是每个节点最多有两个子节点,并且子节点的顺序是有序的,即左子节点在前,右子节点在后。
二叉树的一个重要性质是,对于任意一个节点,它的左子树和右子树都是二叉树。这种递归的定义使得二叉树可以灵活地表示各种数据结构和问题。
二叉树的节点通常由一个包含数据的值和两个指向左子节点和右子节点的指针组成。节点的值可以是任意类型,如整数、字符、对象等。
二叉树可以分为以下几种类型:
- 满二叉树:在满二叉树中,除了叶子节点外,每个节点都有两个子节点,并且所有的叶子节点都在同一层级上。

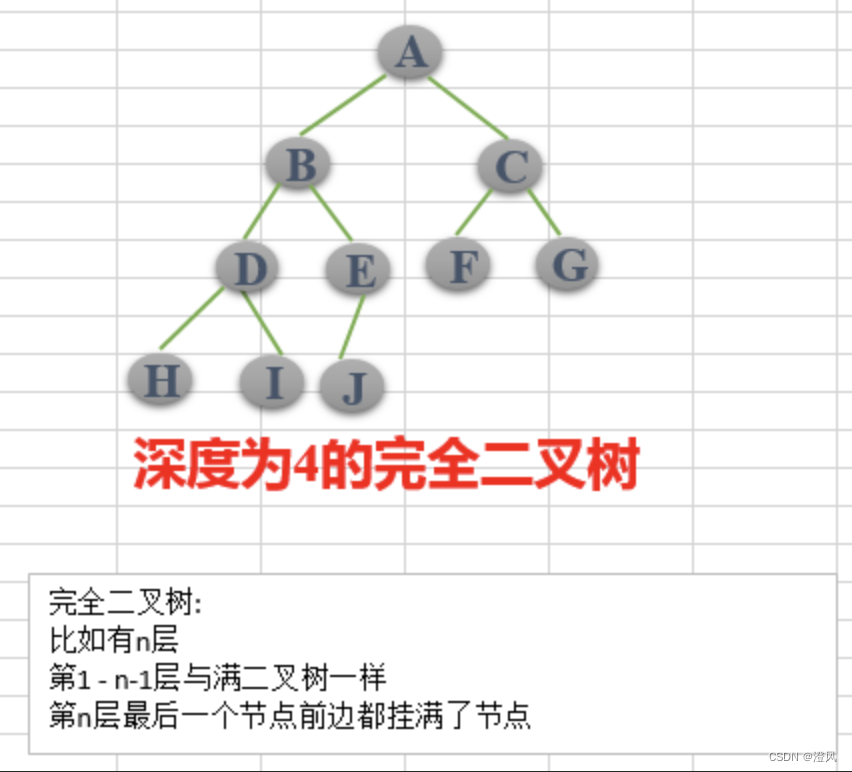
- 完全二叉树:在完全二叉树中,除了最后一层外,其他层的节点都是满的,并且最后一层的节点都靠左排列。
-
二叉搜索树(BST):二叉搜索树是一种特殊的二叉树,其中左子节点的值小于根节点的值,右子节点的值大于根节点的值。这个特性使得二叉搜索树可以高效地进行搜索、插入和删除操作。
-
平衡二叉树:平衡二叉树是一种特殊的二叉树,其中任意节点的左子树和右子树的高度差不超过1。平衡二叉树的目的是保持树的平衡,以提高搜索等操作的效率。
-
(多叉树)B+树:B+树是一种多路搜索树,用于高效地组织和管理大量数据。它具有平衡性和范围查询的优势。B+树的非叶子节点仅存储索引,而叶子节点形成有序链表。这种结构使得B+树在数据库和文件系统等领域广泛应用。它可以减少磁盘IO操作,提高数据的检索效率。通过节点的分裂和合并,B+树保持平衡,避免了树的倾斜。叶子节点按关键字排序,使得范围查询操作高效。B+树的设计可以根据数据规模和访问模式进行调整,适应不同的需求。总之,B+树是一种强大的数据结构,为大规模数据的存储和检索提供了高效的解决方案。
二叉树可以通过多种方式进行遍历,包括前序遍历、中序遍历和后序遍历。这些遍历方式定义了节点的访问顺序,可以用于在二叉树中查找、打印或修改节点的值。
总结起来,二叉树是一种具有两个子节点的树形数据结构,它的灵活性和递归性质使得它在计算机科学中得到广泛应用。
二叉树的java描述和前序遍历、后序遍历、中序遍历
当然!下面是一个简单的二叉树教程,涉及使用Java语言实现二叉树的基本操作。
首先,我们需要定义一个二叉树节点的类,其中包含节点的值、左子节点和右子节点的引用。
class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}
接下来,我们可以实现一些二叉树的基本操作,如插入节点、搜索节点和遍历等。
- 插入节点:
public void insert(TreeNode root, int val) {if (val < root.val) {if (root.left == null) {root.left = new TreeNode(val);} else {insert(root.left, val);}} else {if (root.right == null) {root.right = new TreeNode(val);} else {insert(root.right, val);}}
}
- 搜索节点:
public TreeNode search(TreeNode root, int val) {if (root == null || root.val == val) {return root;}if (val < root.val) {return search(root.left, val);} else {return search(root.right, val);}
}
- 二叉树的遍历(前序、中序和后序):
// 前序遍历(根-左-右)
public void preorder(TreeNode root) {if (root != null) {System.out.print(root.val + " ");preorder(root.left);preorder(root.right);}
}// 中序遍历(左-根-右)
public void inorder(TreeNode root) {if (root != null) {inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}
}// 后序遍历(左-右-根)
public void postorder(TreeNode root) {if (root != null) {postorder(root.left);postorder(root.right);System.out.print(root.val + " ");}
}
现在,我们可以创建一个二叉树的实例并进行操作:
public class BinaryTreeExample {public static void main(String[] args) {BinaryTreeExample example = new BinaryTreeExample();TreeNode root = new TreeNode(5);example.insert(root, 3);example.insert(root, 8);example.insert(root, 2);example.insert(root, 4);System.out.println("前序遍历:");example.preorder(root);System.out.println();System.out.println("中序遍历:");example.inorder(root);System.out.println();System.out.println("后序遍历:");example.postorder(root);System.out.println();int searchValue = 4;TreeNode result = example.search(root, searchValue);if (result != null) {System.out.println("找到节点 " + searchValue);} else {System.out.println("未找到节点 " + searchValue);}}
}
这只是一个简单的二叉树实现示例,你可以根据需要进行扩展和修改。希望这个教程能帮助你理解和实现二叉树的基本操作!
题解
以下是对给定代码的注释和题解:
/*** 通过层次遍历二叉树,将每一层的节点值存储在一个列表中,最后返回所有层的列表。** @param root 根节点* @return 每一层节点值的列表*/
public List<List<Integer>> levelOrder(TreeNode root) {// 创建一个映射表,用于存储每一层的节点值列表Map<Integer, List<Integer>> map = new HashMap<>();// 递归遍历二叉树的每个节点,并将节点值添加到对应层的列表中level(root, 0, map);// 将映射表中的值按层次顺序收集到一个列表中并返回return IntStream.range(0, map.size()).mapToObj(map::get).collect(Collectors.toList());
}/*** 辅助方法,用于递归遍历二叉树的每个节点,并将节点值添加到对应层的列表中。** @param root 当前节点* @param level 当前节点所在的层次* @param map 存储每一层节点值列表的映射表*/
public void level(TreeNode root, int level, Map<Integer, List<Integer>> map) {// 如果当前节点为空,则直接返回if (root == null) {return;}// 获取当前层的节点值列表,如果该层还没有列表,则创建一个新的列表List<Integer> list = map.computeIfAbsent(level, k -> new ArrayList<>());// 将当前节点的值添加到当前层的节点值列表中list.add(root.val);// 递归遍历左子树和右子树,并将层次加一level(root.left, level + 1, map);level(root.right, level + 1, map);
}
题解:
这段代码实现了层次遍历二叉树的功能。它使用递归的方式遍历二叉树的每个节点,并将节点值存储在一个映射表中,其中键表示节点所在的层次,值是一个列表,存储该层的节点值。最后,通过收集映射表中的值,按层次顺序返回所有层的节点值列表。
该算法的时间复杂度是O(n),其中n是二叉树中的节点数。因为我们需要遍历每个节点一次,并将其值添加到对应层的列表中。空间复杂度是O(h),其中h是二叉树的高度,因为我们使用了一个映射表来存储每一层的节点值列表。
总结以及二叉树应用场景
二叉树是一种常见的数据结构,它由节点组成,每个节点最多有两个子节点:左子节点和右子节点。二叉树在许多领域中都有广泛的应用,以下是一些常见的使用场景:
-
搜索和排序:二叉搜索树(BST)是一种特殊的二叉树,它具有以下性质:对于树中的每个节点,其左子树中的所有节点的值都小于它,而右子树中的所有节点的值都大于它。这使得BST非常适合用于搜索和排序操作,例如在数据库中进行索引和检索。
-
表达式求值:二叉表达式树可以用于解析和求值数学表达式。通过将表达式转换为树的形式,可以方便地对表达式进行求值和计算。
-
文件系统:文件系统的目录结构可以用二叉树来表示,其中每个节点代表一个目录或文件,左子节点表示当前目录的子目录,右子节点表示当前目录的兄弟目录。
-
无线路由器:在无线路由器中,二叉树常用于实现路由表。每个节点表示一个IP地址的前缀,左子节点表示匹配该前缀的较长前缀,右子节点表示匹配该前缀的较短前缀。这种结构可以快速查找最匹配的路由。
-
Huffman编码:Huffman编码是一种用于数据压缩的算法,它利用二叉树来构建可变长度编码。频率较高的字符被赋予较短的编码,而频率较低的字符被赋予较长的编码,从而实现数据的高效压缩。
总之,二叉树在搜索、排序、表达式求值、文件系统、网络路由和数据压缩等领域都有广泛的应用。它的灵活性和高效性使得它成为许多问题的解决方案之一。