观看MATLAB技术讲座笔记,该技术讲座视频来自bilibili账号:MATLAB中国。
一、什么是卡尔曼滤波器
卡尔曼滤波器是一种优化估计算法,是一种设计最优状态观测器的方法,其功能为:
- 估算只能被间接测量的变量;
- 通过组合各种可能受噪声影响的传感器测量值,估算系统状态。
通常被应用于制导与导航系统、计算机视觉系统以及信号处理等领域。
卡尔曼滤波器就是一种状态观测器,要想了解什么是卡尔曼滤波器,需要先了解什么是状态观测器。状态观测器用来估计无法直接查看或测量的内容。
二、状态观测器
以下图为例,其中u为系统输入,x为系统状态,x不可直接测量,y为x的间接测量量。 x ^ \hat x x^、 y ^ \hat y y^为x、y的估计值。如果测量值y能与其估计值 y ^ \hat y y^相互匹配,则 x ^ \hat x x^也会与真实的x相吻合。图中蓝色部分即为状态观测器,通过状态观测器,来消除测量值y和估算值 y ^ \hat y y^之间的误差,这样,x的估算值就会与其真实值吻合。
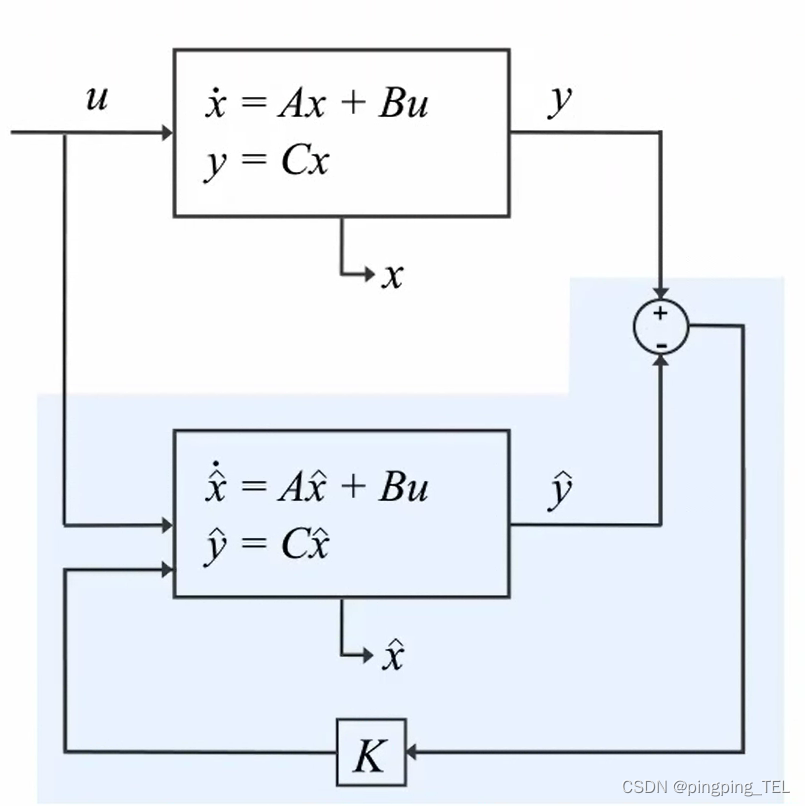
定义 e o b s = x − x ^ e_{obs}=x-\hat{x} eobs=x−x^,由系统和观测器的方程可得:
e ˙ o b s = ( A − K C ) e o b s \dot e_{obs}=(A-KC)e_{obs} e˙obs=(A−KC)eobs
该微分方程的解为:
e o b s ( t ) = e ( A − K C ) t e o b s ( 0 ) e_{obs}(t)=e^{(A-KC)t}e_{obs}(0) eobs(t)=e(A−KC)teobs(0)
那么,如果 ( A − K C ) < 0 (A-KC)<0 (A−KC)<0, e o b s e_{obs} eobs一定会随时间收敛至0,即 x ^ \hat x x^会收敛至 x x x。K可以控制误差函数的衰减率。
三、最优状态估计
以一个简化的汽车模型为例,系统的输入为速度 u k u_k uk,系统状态为汽车的位置 x k x_k xk, y k y_k yk为 x k x_k xk的间接测量输出,这里 C = 1 C=1 C=1。用随机变量 v k v_k vk表示传感器测量噪声,用随机变量 w k w_k wk表示系统过程噪声,可以代表风的影响或汽车速度的变化。假设噪声服从以下高斯分布:
v ∼ N ( 0 , R ) v \sim N(0,R) v∼N(0,R)
w ∼ N ( 0 , Q ) w \sim N(0,Q) w∼N(0,Q)
这里,R、Q为协方差,在这里由于系统为单输出,协方差为标量且等于噪声的方差。
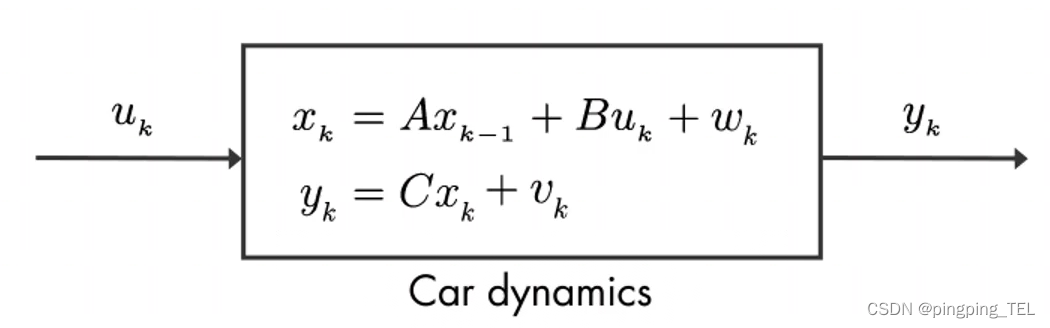
我们可以用汽车数学模型来估算 x k x_k xk,但由于真实系统中过程噪声的存在,这个估算不会是完美的。
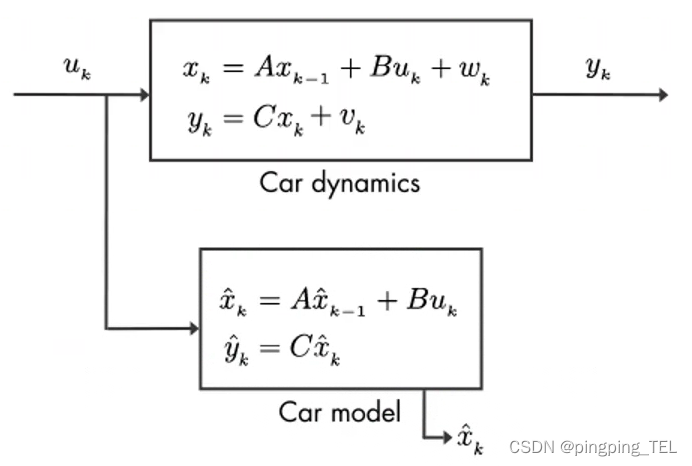
此时,我们有了估算值 x ^ k \hat x_k x^k和测量值 y k y_k yk,其均服从高斯分布。
四、卡尔曼滤波器(KF)
将上述 x ^ k \hat x_k x^k和 y k y_k yk的概率密度函数相乘,得到新的估计值的概率密度函数,同样服从高斯分布,新的方差小于原本的估计值分布的方差,新的均值即为 x k x_k xk的最佳估计。这就是卡尔曼滤波器背后的基本思想,其实现过程如下式所示。
x ^ k = A x ^ k − 1 + B u k + K k ( y k − C ( A x ^ k − 1 + B u k ) ) \hat x_k=A\hat x_{k-1}+Bu_k+K_k(y_k-C(A\hat x_{k-1}+Bu_k)) x^k=Ax^k−1+Buk+Kk(yk−C(Ax^k−1+Buk))
其中, A x ^ k − 1 + B u k A\hat x_{k-1}+Bu_k Ax^k−1+Buk为根据前一时间步估算状态以及当前输入对当前状态的预测,表示为 x ^ k − \hat{x}^{-}_k x^k−,称其为先验估计值,其在使用当前测量值之前计算。上述方程重写为:
x ^ k = x ^ k − + K k ( y k − C x ^ k − ) \hat x_k=\hat{x}^{-}_k+K_k(y_k-C\hat{x}^{-}_k) x^k=x^k−+Kk(yk−Cx^k−)
K k ( y k − C x ^ k − ) K_k(y_k-C\hat{x}^{-}_k) Kk(yk−Cx^k−)使用当前测量值来更新估计值,将最终结果 x ^ k \hat x_k x^k称为后验估计值。
所以可知,卡尔曼滤波器分为预测和更新两个部分。在预测部分计算先验状态预估值和其误差协方差(对于单状态系统即为方差):
x ^ k − = A x ^ k − 1 + B u k \hat{x}^{-}_k=A\hat x_{k-1}+Bu_k x^k−=Ax^k−1+Buk
P k − = A P k − 1 A T + Q {P}^{-}_k=AP_{k-1}A^T+Q Pk−=APk−1AT+Q
在更新阶段,用先验预估值计算后验状态预估值和其误差协方差:
K k = P k − C T C P k − C T + R K_k=\frac{P^-_kC^T}{CP^-_kC^T+R} Kk=CPk−CT+RPk−CT
x ^ k = x ^ k − + K k ( y k − C x ^ k − ) \hat x_k=\hat{x}^{-}_k+K_k(y_k-C\hat{x}^{-}_k) x^k=x^k−+Kk(yk−Cx^k−)
P k = ( I − K k C ) P k − P_k=(I-K_kC)P^-_k Pk=(I−KkC)Pk−
调整卡尔曼滤波增益 K k K_k Kk,使更新后的状态值误差协方差 P k P_k Pk最小。
考虑两种极端情况,当测量噪声方差R为0时,此时 K k = C − 1 K_k=C^{-1} Kk=C−1, x ^ k = y k \hat x_k=y_k x^k=yk,即对状态量的后验估计完全取决于测量值。当先验状态预估值误差协方差 P k − P^-_k Pk−为0时, K k = 0 K_k=0 Kk=0, x ^ k = x ^ k − \hat x_k=\hat{x}^{-}_k x^k=x^k−,即对状态量的后验估计完全取决于先验估计。
综上,用卡尔曼滤波器估计当前状态,需要上一个时间步的后验状态估计值及其误差协方差矩阵和当前测量值。
针对同样的问题,如果有两个传感器(即两个测量值),则卡尔曼滤波器方程为:
x ^ k [ 1 × 1 ] = x ^ k − [ 1 × 1 ] + K k [ 1 × 2 ] ( y k [ 2 × 1 ] − C [ 2 × 1 ] x ^ k − [ 1 × 1 ] ) {\hat x_k}_{[1\times1]}={\hat{x}^{-}_k}_{[1\times1]}+{K_k}_{[1\times2]}({y_k}_{[2\times1]}-C_{[2\times1]}{\hat{x}^{-}_k}_{[1\times1]}) x^k[1×1]=x^k−[1×1]+Kk[1×2](yk[2×1]−C[2×1]x^k−[1×1])
五、非线卡尔曼滤波器
KF仅适用于线性系统,对于如下状态转换函数或观测函数是非线性的系统,需要使用非线性状态估算器。卡尔曼滤波器假设状态服从高斯分布,但高斯分布经非线性变化之后得到的可能不再是高斯分布,卡尔曼滤波器算法可能不会收敛。
x k = f ( x k − 1 , u k ) + w k x_k=f(x_{k-1},u_k)+w_k xk=f(xk−1,uk)+wk
y k = g ( x k ) + v k y_k=g(x_k)+v_k yk=g(xk)+vk
可以使用以下三种非线性状态估算器。
1、扩展卡尔曼滤波器(EKF)
EKF把非线性函数在当前估算状态的平均值附近进行线性化,如下图所示。
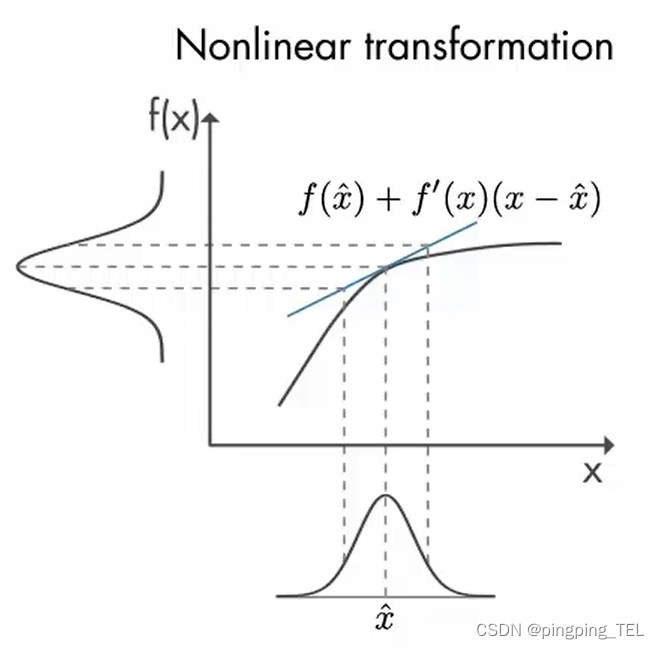
在每个时间步执行线性化,然后将得到的雅可比矩阵用于预测和更新状态。
雅可比矩阵:
F = ∂ f ∂ x ∣ x ^ k − 1 , u k F=\frac{\partial f}{\partial x}|_{\hat x_{k-1},u_k} F=∂x∂f∣x^k−1,uk
G = ∂ g ∂ x ∣ x ^ k G=\frac{\partial g}{\partial x}|_{\hat x_k} G=∂x∂g∣x^k
线性化系统:
Δ x k ≈ F Δ x k − 1 + w k \Delta x_k\approx F\Delta x_{k-1}+w_k Δxk≈FΔxk−1+wk
Δ y k ≈ G Δ x k + v k \Delta y_k\approx G\Delta x_k+v_k Δyk≈GΔxk+vk
EKF缺点如下:
- 如果有复杂的导数存在,可能难以解析计算雅可比矩阵;
- 如果以数值方式计算雅可比矩阵可能需要很高的计算成本;
- EKF不适用于具有不连续模型的系统,因为系统不可微分时雅可比矩阵不存在;
- 高度非线性系统的线性化效果不好,非线性函数可能不能通过线性函数很好的近似表达出来。换言之,使用EKF需要非线性系统本身能够很好的进行线性化。
2、无迹卡尔曼滤波器(UKF)
UKF不像EKF那样近似非线性函数,其近似概率分布。UKF选择一组最小的采样点(称为sigma点),让它们均值与协方差和要近似的分布一致,且sigma围绕均值对称分布。将sigma进行非线性变化,计算变化后的点的均值和协方差,用来确定确定新的高斯分布,计算新的状态值。
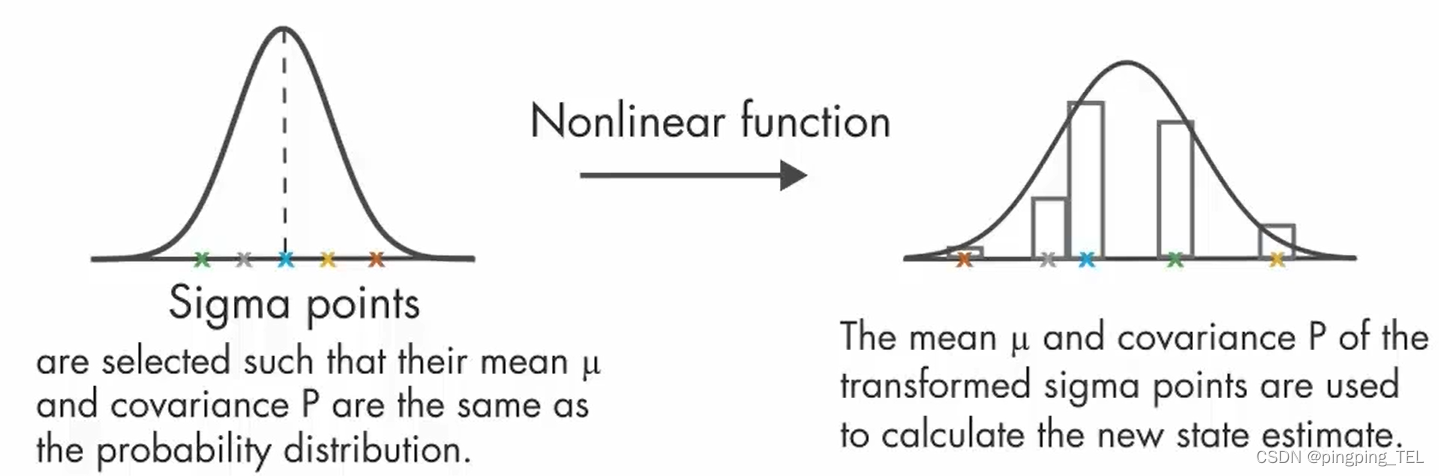
粒子滤波器(PF)与UKF原理类似,其使用的样本点称为粒子。但与UKF不同,PF近似任意分布。为了表示未明确知道的任意分布,PF所需的粒子数远大于UKF。