链表part2
1)两两交换链表中的节点
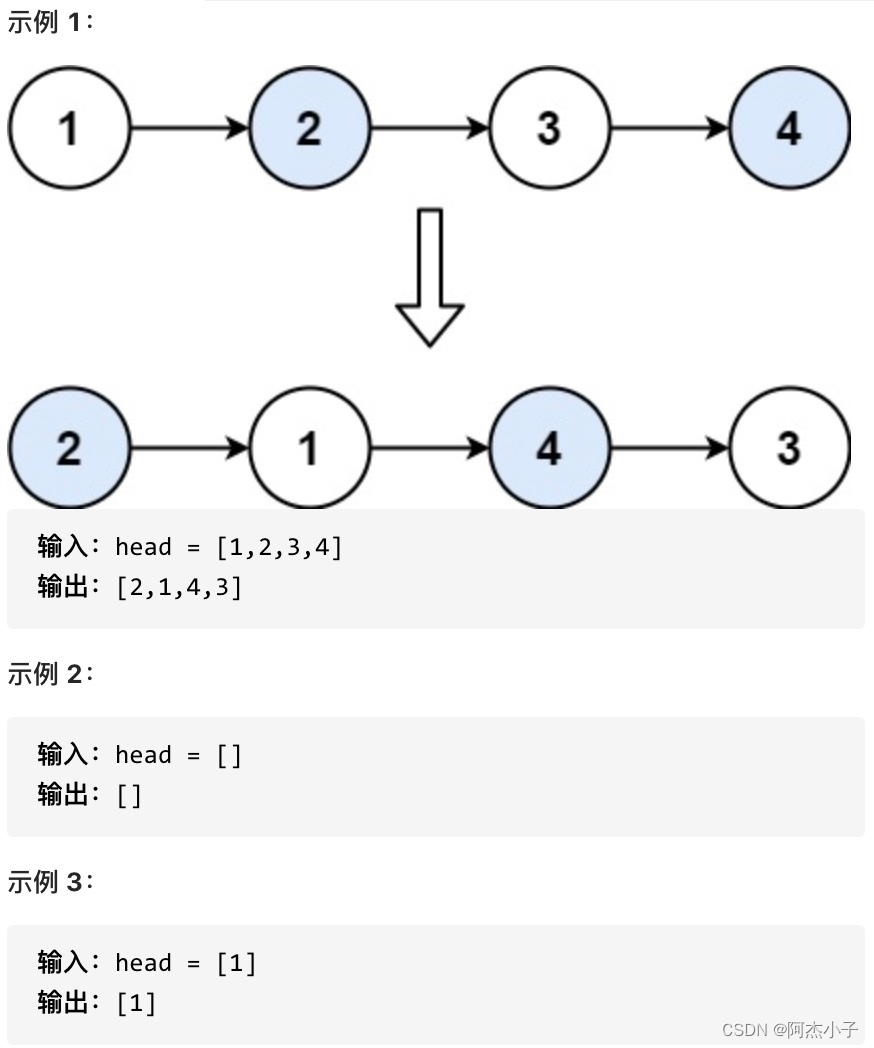
这道题按照三步走方式:
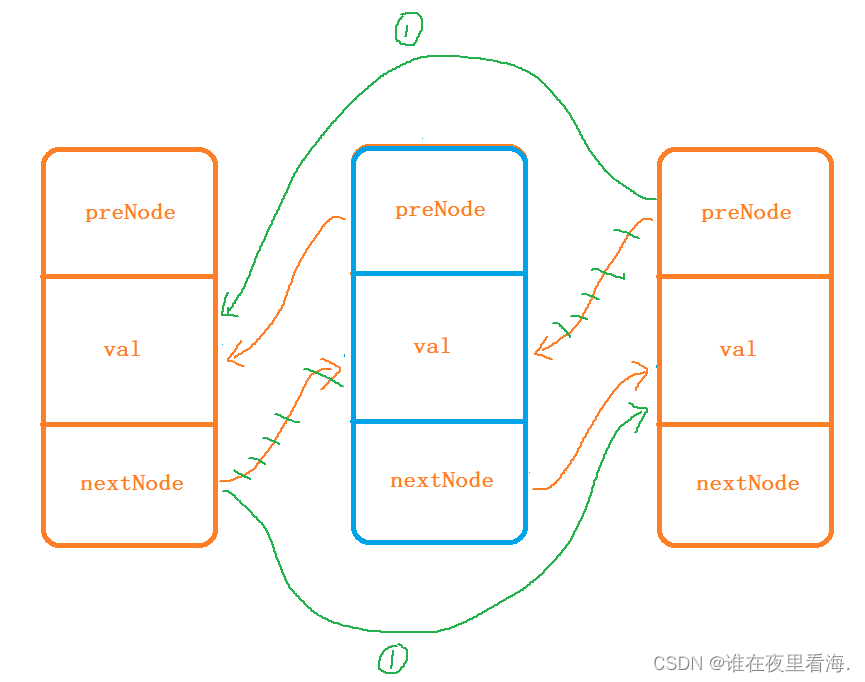
(1)第一步,设置cur指针指向这两个元素的第一个(这里一定要注意保存原结点!),断开cur与第一个节点的链接,指向第二个元素。cur->next = cur->next->next
(2)第二步,此时得到的链表结构为:<cur>——><2>——><3>,<1>——><2>,因此,此时需要将2与3之间的链接断开,使得2指向1。cur->next->next = temp->next
(3)第三步,链接1与3:cur->next->next->next = temp->next->next->next
小细节的话就是使用虚拟结点指向头结点,同时循环的终止条件是最后指向的两个指针不能为空,因为我们需要两两交换。
class solution{
public:ListNode* swapParis(ListNode* head){ListNode* dummyHead = new ListNode(0);dummyHead->next = head;ListNode* cur = dummyHead;while(cur->next != nullptr && cur->next->next != nullptr){ListNode* temp = cur;cur->next = cur->next->next; // 步骤一cur->next->next = temp->next; // 步骤二cur->next->next->next = temp->next->next->next; // 步骤三cur = cur->next->next;}ListNode* result = dummyHead->next;delete dummyHead;return result;}
};
2)删除链表的倒数第N个节点
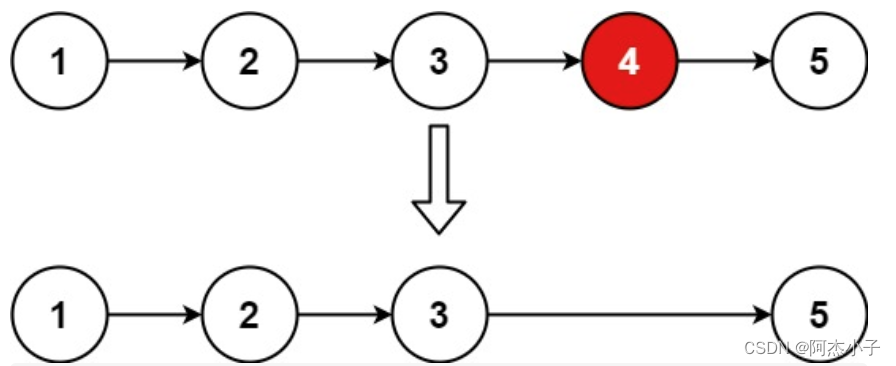
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5] 示例 2:
输入:head = [1], n = 1 输出:[] 示例 3:
输入:head = [1,2], n = 1 输出:[1]
双指针的方法,好像这里用它的原因是如果我们要寻找倒数第n个,那么我们要先走到最末尾,然后再倒序寻找,因此这里用两个指针(也可以看作固定的窗长),给出文档里的题解步骤:
- 定义fast指针和slow指针,初始值为虚拟头结点,如图:
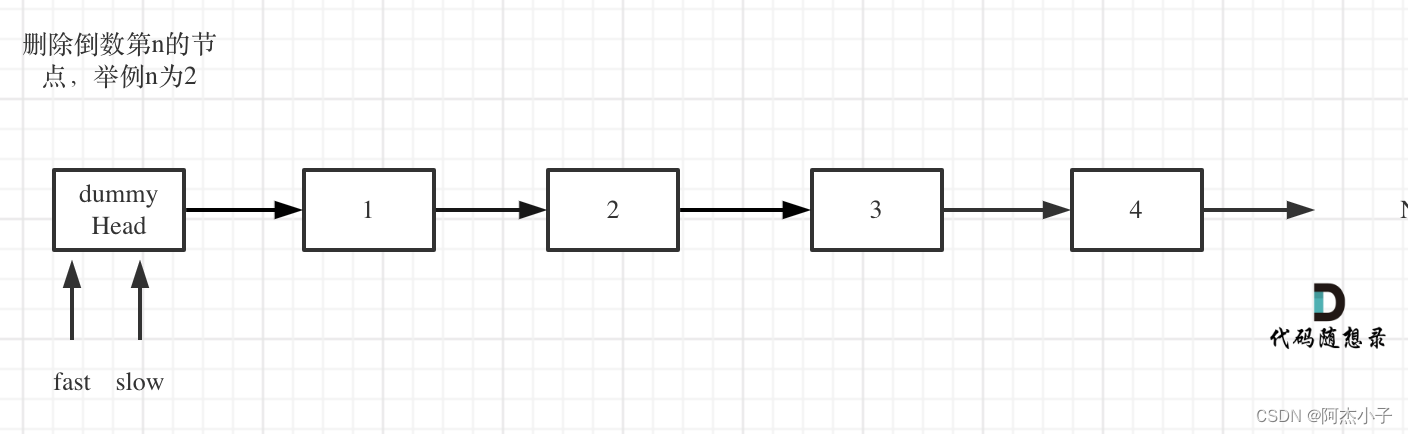
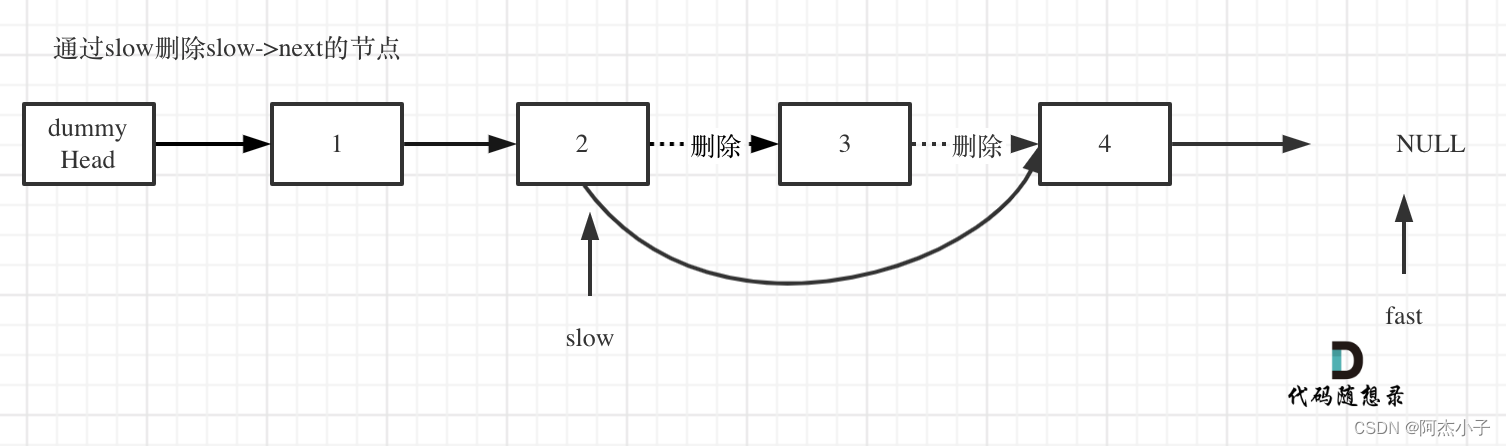
- fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
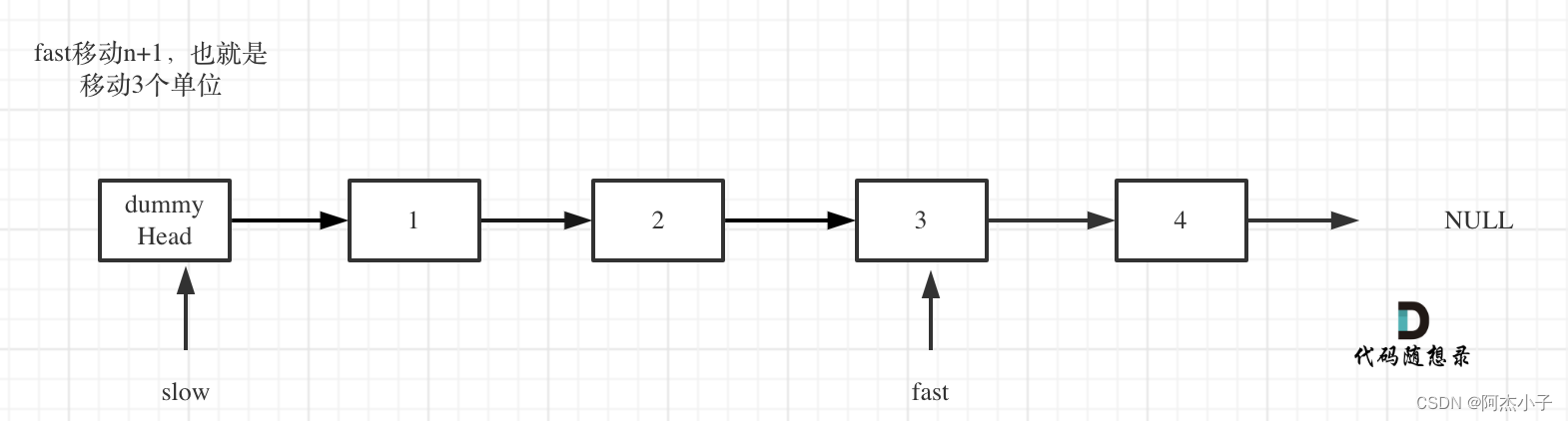
- fast和slow同时移动,直到fast指向末尾,如题:
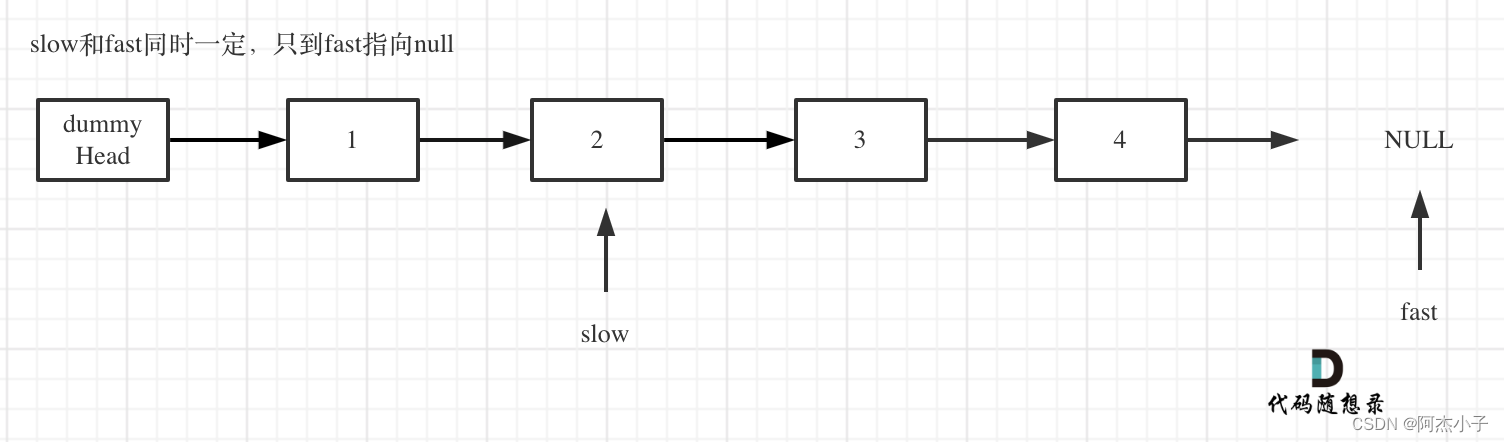
- 删除slow指向的下一个节点,如图:
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* dummyHead = new ListNode(0);dummyHead->next = head;ListNode* slow = dummyHead;ListNode* fast = dummyHead;while(n-- && fast != NULL) {fast = fast->next;}fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点while (fast != NULL) {fast = fast->next;slow = slow->next;}slow->next = slow->next->next; // ListNode *tmp = slow->next; C++释放内存的逻辑// slow->next = tmp->next;// delete tmp;return dummyHead->next;}
};
3)链表相交问题
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。图示两个链表在节点 c1 开始相交:
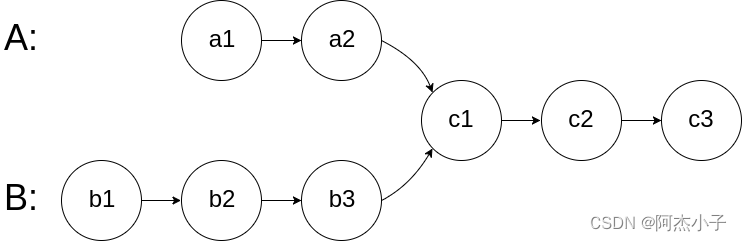
思路很简单:长的链表先遍历,遍历到剩余的结点数与短链表一至即可。
这里需要两个指针,一个指向A,一个指向B。
class solution{
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB){ListNode* curA = headA;ListNode* curB = headB;int lenA = 0, lenB = 0;while(curA!=NULL){lenA++;curA = curA->next;}while(curB!=NULL){lenB++;curB = curB->next;}curA = headA;curB = headB;if(lenB > lenA){swap(lenA, lenB);swap(curA, curB);}int gap = lenA - lenB;while(gap--){curA = curA->next;}while(curA != NULL){if(curA == curB){return curA;}curA = curA->next;curB = curB->next;}return NULL; }
};
4)环形链表2
这题把我CPU干烧了,直接看carl的解答吧
判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的。
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针。
会发现最终都是这种情况, 如下图:
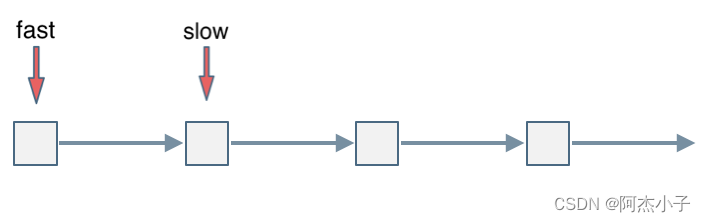
fast和slow各自再走一步, fast和slow就相遇了
这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合。
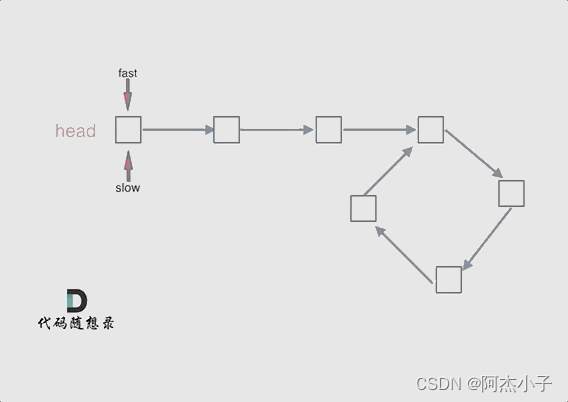
如果有环,如何找到这个环的入口
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
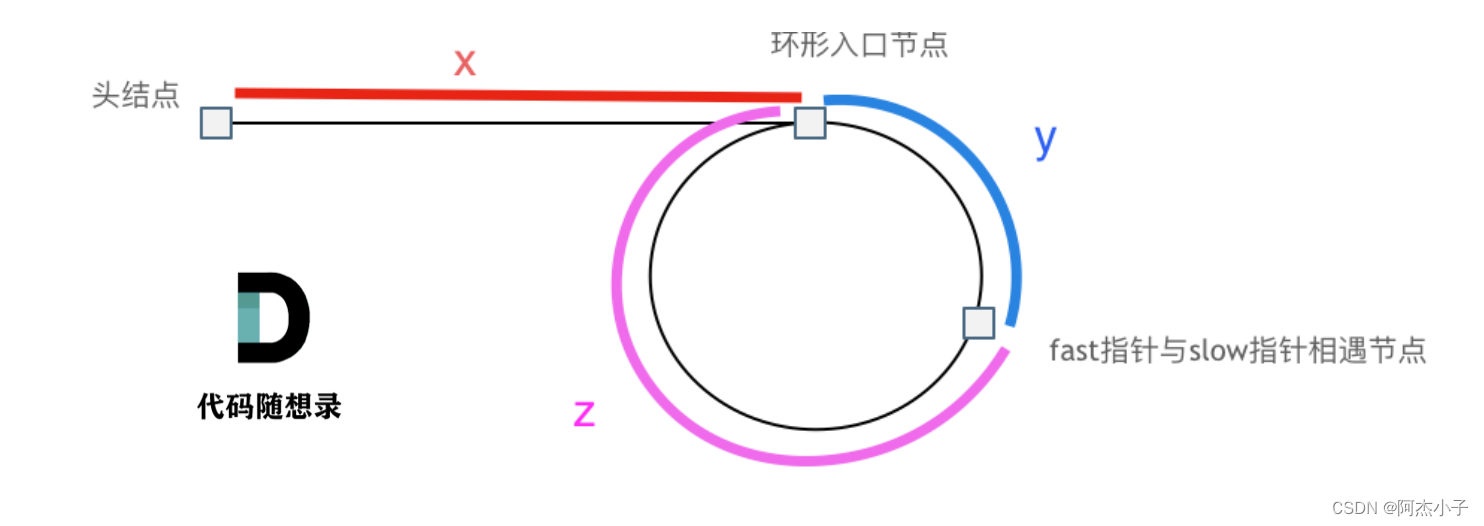
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针,{y+z)为一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点,所以 fast指针走过的节点数 = slow指针走过的节点数*2:(x + y) * 2 = x + y + n (y + z)。两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示头结点到环形入口节点的的距离。所以要求x ,将x单独放在左面:x = n (y + z) - y ,再从n(y+z)中提出一个(y+z)来,整理公式之后为如下公式:x = (n -1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是环形入口的节点。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。让index1和index2同时移动,每次移动一个节点,那么他们相遇的地方就是环形入口的节点。
n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候 效果是一样的,一样可以通过这个方法找到 环形的入口节点,只不过,index1 指针在环里 多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while(fast != NULL && fast->next != NULL) {slow = slow->next;fast = fast->next->next;// 快慢指针相遇,此时从head 和 相遇点,同时查找直至相遇if (slow == fast) {ListNode* index1 = fast;ListNode* index2 = head;while (index1 != index2) {index1 = index1->next;index2 = index2->next;}return index2; // 返回环的入口}}return NULL;}
};