# 图可以根据边的性质进行分类：
# 有向图（Directed Graph）：在有向图中，边是有方向性的，从一个节点指向另一个节点。这意味着从节点 A 到节点 B 的边与从节点 B 到节点 A 的边可以是不同的，或者根本不存在。有向图通常用于表示具有方向性的关系，例如网页链接、社交关系中的关注关系等。
# 无向图（Undirected Graph）：在无向图中，边是没有方向性的，即连接两个节点的边没有箭头指示方向。这意味着节点 A 与节点 B 之间的关系是对称的，从 A 到 B 的边与从 B 到 A 的边是相同的。无向图通常用于表示无方向性的关系，例如交通网络、好友关系等。
# 权重图（Weighted Graph）：在权重图中，每条边都有一个与之关联的权重或值。这些权重可以表示连接两个节点的成本、距离、容量等信息。权重图通常用于模拟具有不同代价或度量的关系，例如路线规划中的道路长度、社交网络中的强度等。
# 无权图（Unweighted Graph）：与权重图相反，无权图中的边没有相关的权重信息。它们只表示节点之间的连接关系，而不考虑连接的强度或成本。
# 这些不同类型的图可以根据问题的需求进行选择和应用，以更好地描述和解决特定领域的问题。

-------

当我们考虑一个简单的社交网络，其中有几个人以及它们之间的友谊关系时，我们可以使用无向图来表示这种关系。

假设我们有以下人物：

- Alice
- Bob
- Charlie
- David

他们之间的友谊关系如下：

- Alice 和 Bob 是朋友。
- Bob 和 Charlie 是朋友。
- Charlie 和 David 是朋友。

用无向图表示这个社交网络，节点代表人，边代表友谊关系。

这个无向图可以用以下方式表示：

节点集合 V = {Alice, Bob, Charlie, David}

边集合 E = {{Alice, Bob}, {Bob, Charlie}, {Charlie, David}}

这里的每一对节点都表示一个边，例如 {Alice, Bob} 表示 Alice 和 Bob 之间存在一条友谊边，而 {Bob, Charlie} 表示 Bob 和 Charlie 之间也存在一条友谊边。这些边都是无向的，因此没有方向性。

class UndirectedGraph:def __init__(self):self.adjacency_list = {}def add_vertex(self, vertex):if vertex not in self.adjacency_list:self.adjacency_list[vertex] = []def add_edge(self, vertex1, vertex2):if vertex1 in self.adjacency_list and vertex2 in self.adjacency_list:self.adjacency_list[vertex1].append(vertex2)self.adjacency_list[vertex2].append(vertex1)  # 更新顶点 vertex2 的邻接列表else:print("One or both vertices do not exist.")# 在你提供的代码中，add_edge() 方法用于向图中添加一条边。让我解释一下这段代码的作用：
# if vertex1 in self.adjacency_list and vertex2 in self.adjacency_list:：这个条件检查 vertex1 和 vertex2 是否都存在于图的顶点列表中。只有当两个顶点都存在时，才执行接下来的操作。
# self.adjacency_list[vertex1].append(vertex2)：这一行将 vertex2 添加到 vertex1 的邻接列表中，表示顶点 vertex1 与顶点 vertex2 之间有一条边。
# self.adjacency_list[vertex2].append(vertex1)：这一行实际上是为了保证无向图的连通性，将 vertex1 添加到 vertex2 的邻接列表中，表示顶点 vertex2 与顶点 vertex1 之间也有一条边。这样做是因为无向图的边是双向的，如果有从 vertex1 到 vertex2 的边，也就意味着有从 vertex2 到 vertex1 的边。
# 通过这种方式，add_edge() 方法确保了图是无向图，即添加边的操作同时更新了两个顶点的邻接列表，使得图中的边是双向的。def display_graph(self):print("Adjacency List:")for vertex, neighbors in self.adjacency_list.items():print(f"{vertex}: {neighbors}")print("\nGraph:")for vertex in self.adjacency_list:print(vertex, end=" -> ")print(" -> ".join(self.adjacency_list[vertex]))# 这段代码是用来打印图的边的。让我解释一下：
# for vertex in self.adjacency_list:：这个循环遍历图中的每个顶点，vertex 变量在每次迭代中都代表一个顶点名称。
# print(vertex, end=" -> ")：这一行打印当前顶点的名称，然后用箭头符号 "->" 结束输出，使得下一个顶点的名称在同一行显示。
# print(" -> ".join(self.adjacency_list[vertex]))：这一行使用 join() 方法将当前顶点的邻接列表连接成一个字符串，并使用箭头符号 "->" 将它们分隔开。然后，将连接后的字符串打印出来，显示当前顶点与其相邻顶点之间的连接关系。
# 所以，这段代码实际上是在打印图的邻接表，以边的形式显示图的结构。
# string.join(iterable)是一个字符串方法，用于将可迭代对象中的元素连接成一个字符串;
# string 是用来连接元素的字符串，而 iterable 则是要连接的可迭代对象，通常是列表或元组# 创建一个无向图对象
graph = UndirectedGraph()# 添加顶点
graph.add_vertex("Alice")
graph.add_vertex("Bob")
graph.add_vertex("Charlie")
graph.add_vertex("David")# 添加边 /输出的顺序与添加边的顺序有关。
graph.add_edge("Alice", "Bob")
graph.add_edge("Bob", "Charlie")
graph.add_edge("Charlie", "David")# 显示图
graph.display_graph()# 图可以根据边的性质进行分类：
# 有向图（Directed Graph）：在有向图中，边是有方向性的，从一个节点指向另一个节点。这意味着从节点 A 到节点 B 的边与从节点 B 到节点 A 的边可以是不同的，或者根本不存在。有向图通常用于表示具有方向性的关系，例如网页链接、社交关系中的关注关系等。
# 无向图（Undirected Graph）：在无向图中，边是没有方向性的，即连接两个节点的边没有箭头指示方向。这意味着节点 A 与节点 B 之间的关系是对称的，从 A 到 B 的边与从 B 到 A 的边是相同的。无向图通常用于表示无方向性的关系，例如交通网络、好友关系等。
# 权重图（Weighted Graph）：在权重图中，每条边都有一个与之关联的权重或值。这些权重可以表示连接两个节点的成本、距离、容量等信息。权重图通常用于模拟具有不同代价或度量的关系，例如路线规划中的道路长度、社交网络中的强度等。
# 无权图（Unweighted Graph）：与权重图相反，无权图中的边没有相关的权重信息。它们只表示节点之间的连接关系，而不考虑连接的强度或成本。
# 这些不同类型的图可以根据问题的需求进行选择和应用，以更好地描述和解决特定领域的问题。

Adjacency List:
Alice: ['Bob']
Bob: ['Alice', 'Charlie']
Charlie: ['Bob', 'David']
David: ['Charlie']

Graph:
Alice -> Bob
Bob -> Alice -> Charlie
Charlie -> Bob -> David
David -> Charlie
[Finished in 603ms]

无向图可以使用多种方式来进行存储，其中两种最常见的方式是邻接列表和邻接矩阵。

1. **邻接列表（Adjacency List）**：
   邻接列表是一种将图中每个节点的邻居节点列表存储起来的方式。对于每个节点，将其邻居节点以列表、链表或其他数据结构的形式存储在该节点的条目中。这种方式可以有效地节省空间，尤其适用于稀疏图，即节点之间的边相对较少的情况。Python 中可以使用字典或哈希表来实现邻接列表。

2. **邻接矩阵（Adjacency Matrix）**：
   邻接矩阵是一个二维数组，其中行和列分别代表图中的节点，矩阵的元素表示节点之间是否存在边。如果节点 i 和节点 j 之间存在边，则矩阵的第 i 行和第 j 列的元素为 1；否则为 0。这种方式相对于邻接列表来说更加直观，但是在图比较稀疏的情况下会浪费大量的空间。

在前面的代码示例中，我使用了邻接列表来存储无向图。每个节点都有一个列表，其中存储了与该节点相邻的其他节点。

----------

邻接矩阵是一种常见的图的表示方法，尤其适用于稠密图，因为它提供了直观的方式来表示节点之间的连接关系。下面是如何使用邻接矩阵来表示你提供的社交网络：

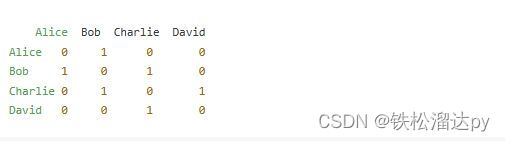
在这个邻接矩阵中，每一行和每一列分别代表一个节点，而矩阵中的值表示节点之间是否存在边。例如，第一行表示 Alice 与其他节点的连接关系，其中 1 表示 Alice 与 Bob 相连，而其他值为 0 表示 Alice 与 Charlie 和 David 不相连。

这种表示方式虽然直观易懂，但在图比较稀疏的情况下会占用大量的空间，因为矩阵的大小与节点数量的平方成正比。相对而言，邻接列表在这种情况下可能更为高效，因为它只需要存储实际存在的边。

class SocialNetwork:def __init__(self, num_nodes):self.num_nodes = num_nodesself.adj_matrix = [[0] * num_nodes for _ in range(num_nodes)]
# 这段代码在 SocialNetwork 类的构造函数中初始化了社交网络的属性：
# self.num_nodes = num_nodes: 这一行将社交网络的节点数量设置为传入的参数 num_nodes。这样，我们就可以知道社交网络有多少个节点。
# self.adj_matrix = [[0] * num_nodes for _ in range(num_nodes)]: 这一行创建了一个大小为 num_nodes × num_nodes 的二维列表（即矩阵），并将其用于表示社交网络的邻接矩阵。初始时，所有的边都被设置为 0，表示没有边相连。
# 通过这两行代码，我们在创建 SocialNetwork 对象时就初始化了社交网络的基本结构，为后续添加边和展示邻接矩阵做好了准备。def add_edge(self, node1, node2):if node1 < self.num_nodes and node2 < self.num_nodes:self.adj_matrix[node1][node2] = 1self.adj_matrix[node2][node1] = 1else:print("Invalid node index.")# 这段代码是用来在邻接矩阵中添加边的方法。让我解释一下它的工作原理：
# 首先，检查给定的节点索引 node1 和 node2 是否有效，即它们是否在社交网络的节点范围内。
# 如果节点索引有效，则将邻接矩阵中索引为 (node1, node2) 和 (node2, node1) 的位置的值设为 1，表示节点 node1 和 node2 之间存在一条边。
# 这里之所以要同时设置 (node1, node2) 和 (node2, node1) 的值是因为这是一个无向图，边不区分方向，所以节点 node1 和 node2 之间的连接关系是相互的。
# 这样，当我们调用add_edge(0, 1)时，会将邻接矩阵中的 (0, 1) 和 (1, 0) 的位置的值都设为 1，表示 Alice 和 Bob 之间存在一条边。def display_adj_matrix(self):for row in self.adj_matrix:print(" ".join(map(str, row)))# 创建一个包含4个节点的社交网络
social_network = SocialNetwork(4)# 添加边
social_network.add_edge(0, 1)  # Alice 和 Bob 是朋友
social_network.add_edge(1, 2)  # Bob 和 Charlie 是朋友
social_network.add_edge(2, 3)  # Charlie 和 David 是朋友# 显示邻接矩阵
print("邻接矩阵表示的社交网络:")
social_network.display_adj_matrix()# [[0] * num_nodes for _ in range(num_nodes)]
# 这行代码是一个列表推导式，用于创建一个二维列表（矩阵），其维度为 num_nodes × num_nodes。让我解释一下它的工作原理：# [[0] * num_nodes for _ in range(num_nodes)]: 这一整个表达式是一个嵌套的列表推导式。外层的 for _ in range(num_nodes) 循环了 num_nodes 次，每次都会生成一个包含 num_nodes 个 0 的列表。这样就生成了一个 num_nodes × num_nodes 的二维列表，其中每个元素都是 0。# 总的来说，这段代码的作用是创建一个大小为 num_nodes × num_nodes 的二维列表，并将其初始化为全 0，用于表示社交网络的邻接矩阵。

 邻接矩阵表示的社交网络:
0 1 0 0
1 0 1 0
0 1 0 1
0 0 1 0
[Finished in 563ms]