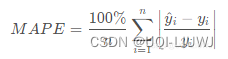参考文献：

[1] Lei S , Chen C , Zhou H ,et al.Routing and Scheduling of Mobile Power Sources for Distribution System Resilience Enhancement[J].IEEE Transactions on Smart Grid, 2019:5650-5662.DOI:10.1109/TSG.2018.2889347.

        这篇博客是上述SCI一区论文的部分复现，即采用两阶段鲁棒优化求解应急移动电源预配置方案的部分。

1.摘要

        移动式电源（MPSs）包括电动汽车（EV）车队、车载移动能量存储系统（MESSs）和移动应急发电机（MEGs），具有极大潜力增强配电系统（DS）对极端天气事件的韧性。然而，它们的派遣并没有得到深入的研究。本文通过一个两阶段框架实施MPS的韧性配置和调度。在第一阶段，即事件发生前，MPS被预置在DS中，以实现快速的预恢复，从而增强对关键负载的电力供应的可持续性。DS网络也被积极重新配置为受影响较小或压力较小的状态。构建了一个两阶段的鲁棒优化模型，并通过列-约束生成算法来得出第一阶段的决策。在第二阶段，即事件发生后，MPS在DS中被动态调度，以配合传统的恢复工作，从而增强系统的恢复能力。制定了一个新颖的混合整数规划模型，用于优化MPS的动态调度，解决了MPS派遣和DS运行等不同时间尺度之间的耦合，以及道路和电力网络的耦合等问题。在IEEE 33节点和123节点测试系统上进行的案例研究证明了所提出的方法在提高DS韧性方面在MPS路由和调度方面的有效性。

2.原理介绍

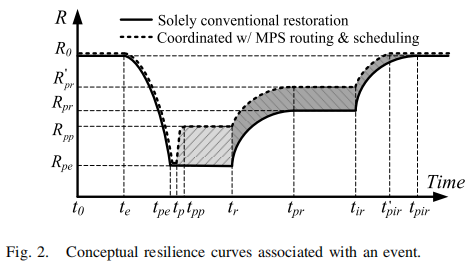
        本文详细阐述了配电网韧性曲线。在图2中，R是系统韧性水平的度量。伴随极端天气事件，配电系统经历以下状态：韧性状态 t0∼te，事件进展 te∼tpe，事件后退化状态 tpe∼tr，恢复状态 tr∼tpr，修复后状态 tpr∼tir，基础设施恢复 tir∼tpir。需要注意的是，事件发生后的系统恢复是一个多阶段的过程。在典型和主要的修复和恢复阶段之前，可以立即进行快速的预恢复，例如连接应急备用发电机。通过预恢复，事件后的状态 tpe∼tr 可以进一步分为三个阶段：事件后的状态 tpe∼tp，预恢复状态 tp∼tpp（进行预恢复时），和预恢复后状态 tpp∼tr（预恢复后的状态）。

        本文提出了一个两阶段框架，用于实施移动式电源（MPSs）的韧性路由和调度。在第一阶段，即事件发生前 t0∼te，MPSs被主动预置到DS的一些选定节点，以增强系统的生存能力。在这里，我们通过 tpe∼tr 期间的系统韧性水平来评估生存能力。预置的MPSs能够快速进行系统的预恢复。事件发生后不久，在 tp 时刻，MPSs可以连接到DS，迅速将系统的韧性水平从 Rpe 提升到 Rpp。DS的网络重新配置也被协同优化，将系统转变为受事件影响较小、压力较小的状态[34]。通过这些措施，在事件后的状态，即系统的生存能力水平在 tpp∼tr 期间从 Rpe 提升到 Rpp，如图2所示。相比之下，如果没有MPSs等，系统的事件后韧性水平必须一直保持在 Rpe 直到 tr 时刻。

        在第二阶段，即事件发生后，MPSs被动态调度，以配合修复和基础设施恢复工作，以增强系统在 tr∼tpir 期间的恢复能力。这里的恢复类似于[9]提出的度量方法，用于评估系统的快速恢复程度。MPSs的交通运输和电力调度、DS的动态网络重新配置和功率调度等都被协同优化。因此，在恢复后的状态，系统的韧性水平从 Rpr 提升到 Rpr，并且系统的负载可以在比 tpir 更早的 tpir 时刻得到完全恢复。

2.1 MPS的预配置

        在极端天气事件发生前，MPSs被预置在配电系统中，以提升其生存能力，这里以关键负载的电力供应情况来衡量。我们提出了一个两阶段鲁棒优化模型来确定预置计划。其目标是最大化 t=0 时刻（即此处的 tpp）生存负载的最坏情况加权和：

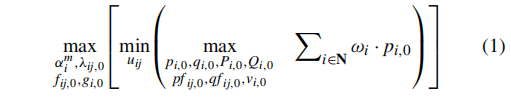
        最外层的优化协调了MPSs的预置节点和DS的拓扑结构。也就是说，配电网重构也被采用以协调MPSs的预置，以更好地利用MPSs增强DS生存能力的潜力。在事件发生前，EV和MESS充分充电，并且MEG在事件之前被加注燃料，预置的MPSs在事件后的短时间内便快速连接到系统供电。最外层涉及的变量受以下约束条件的限制：

        约束（2）强制每个MPS只能预置到其候选节点中的一个。。应急发电机和移动能量存储系统可以连接到带有MESS站点的节点，而电动车车队则可以连接到带有充电站的节点。约束（3）限制了连接到每个站点的MPSs的数量。这个限制可以设置为站点的容量，或者对于所有站点设置为1，以确保更分散的预置，通常更具有韧性。约束（4）-（6）共同确保DS的径向性。在这方面，其拓扑结构需要满足两个条件：1）它有N−Nsub.条支路关闭；2）每个负载节点连接到一个变电站节点。方程（4）表示第一个条件。将变电站节点和负载节点分别视为虚拟流的源和汇。然后，通过强制每个负载节点从一个源节点获得一单位的虚拟流，来满足第二个条件。方程（5）确保所有负载节点满足虚拟流平衡。在这里，指的是虚拟流li,0，它表示流入负载节点的虚拟流量为1。约束（6）限制了未连接的支路上的虚拟流为零。设置K1 = N−Nsub.足够大。有关使用虚拟网络构建径向性约束的更多细节，请参阅[39]。为了避免单个变电站节点孤立，还添加了以下约束：

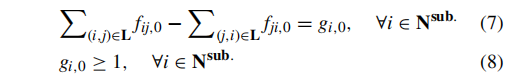
        对于没有零负载节点或分布式发电的配电系统，不需要引入虚拟流，因为功率流约束将自然地强制满足前述的第二个条件。在这项工作中，我们的配电系统中有MPSs，因此引入了虚拟流和相关概念。在两阶段鲁棒优化模型的中层中，针对最外层得出的第一阶段MPSs预置和DS重构决策，我们寻求能够最小化生存负载的加权和的一组受损支路。支路损坏受到以下约束的限制：

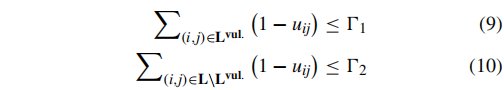
        最内层通常被称为第二阶段的recourse问题。在最外层得出的第一阶段决策和中间层的系统损坏情况的基础上，通过以下约束最大化生存负载的加权和：

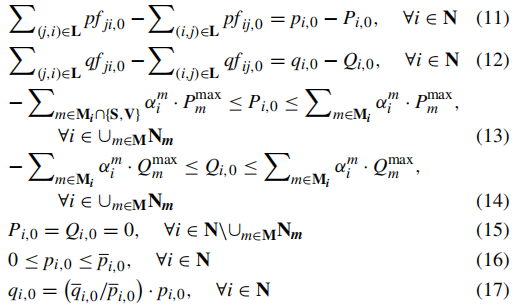
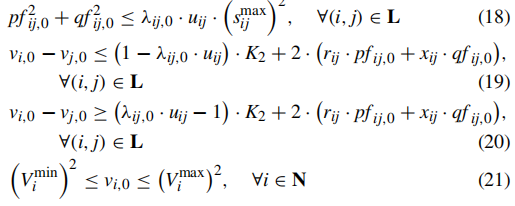
        方程（11）和（12）分别强制所有节点满足实功和无功平衡条件。约束（13）和（14）分别限制了候选节点对MPS连接的实功和无功注入或提取。对于候选节点，其实/无功注入/提取限制是连接到它的MPSs的实/无功容量之和。由于事件导致多次损害，使电网分裂成岛屿，MPSs通常只在预恢复阶段注入电力[32]，特别是对于失去主要电网电力的岛屿。约束（15）对于不用于MPS连接的节点强制零功率输出。在这项工作中，最终用电客户简单地被视为负载。约束（16）规定了每个受影响节点的生存负载范围。方程（17）假设了电力需求的固定功率因数。约束18限制了每条支路的视在功率不超过其容量，并强制未连接的支路上的实功和无功流为零。约束（19）和（20）基于DistFlow模型[41]表达了功率流方程。忽略了较小的二次项[41]。使用足够大的正数K2放松了这些与未连接的支路相关的约束。约束（18）-（20）涉及术语λ_ij,0·u_ij。它们不需要线性化。由于λ_ij,0和u_ij分别位于两阶段鲁棒优化模型的外部和中层，这些术语实际上不会为第V-A节的解算法引入非线性。约束（21）表示电压幅值限制。

2.2求解算法

        1）C&CG算法

        MPS预定位模型是一个两阶段的鲁棒优化问题。我们使用列与约束生成算法（C&CG）来解决它。为了简洁明了起见，我们将MPS预定位模型改写为紧凑的形式：

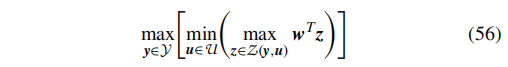
        其中，y、u 和 z 分别是第一阶段决策变量（MPS预定位和网络重构）、不确定性变量（支路损坏），以及第二阶段决策变量（电力分配）。它们的可行域分别表示为Y、U 和 Z(y, u)，并由约束（2）-（8）、（9）-（10）和（11）-（21）定义。

        将最内层max问题进行对偶变换，并将其与中层min问题相结合，（56）中的min-max子问题（SP）变成：

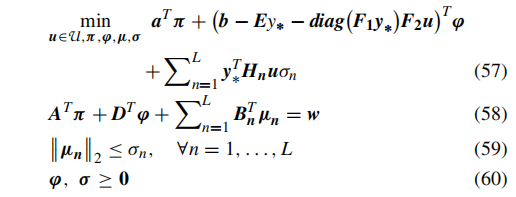
其中y∗是一个给定的变量y取值；π，ϕ，μ和σ是对偶变量。主问题（MP）如下：

        其中，K为迭代次数。因此，可以使用C&CG算法进行迭代求解。

        2）线性化技术

        Min-max子问题的目标函数（57）包含二元变量乘以连续变量的双线性项。方程（46）-（47）也以这种形式包含双线性项。这些非线性项可以被线性化。例如，我们可以用下面的约束来替换方程（46）中的 βim,t×cpm,t 项：

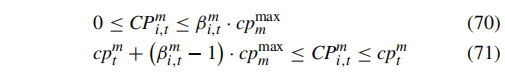
        在进行了这样的线性化之后，通过算法1解决MPS预定位问题和MPS动态调度问题时，涉及的MP和SP都变成了混合整数二阶锥规划（MISOCP）模型。如果约束（18）和（52）也线性化了，那么遇到的优化问题就变成了混合整数线性规划（MILP）模型。MISOCP和MILP问题都可以通过许多现成的求解器，如Gurobi，进行高效求解。

3.编程思路

3.1参数和变量定义

表1 相关参数

表2 决策变量

3.2编程思路

        根据对文献内容的解读，可以设计下面的编程思路：

步骤1：输入所需数据

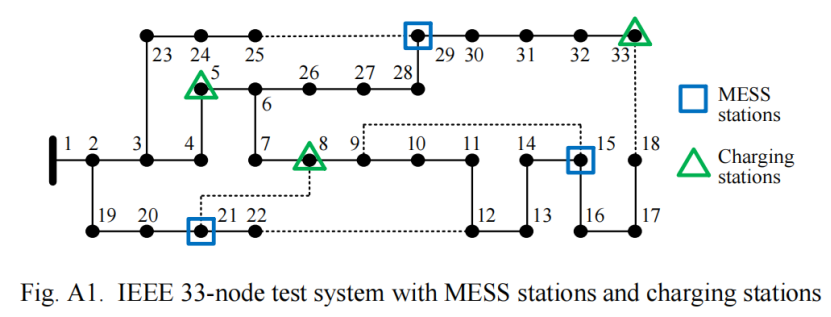
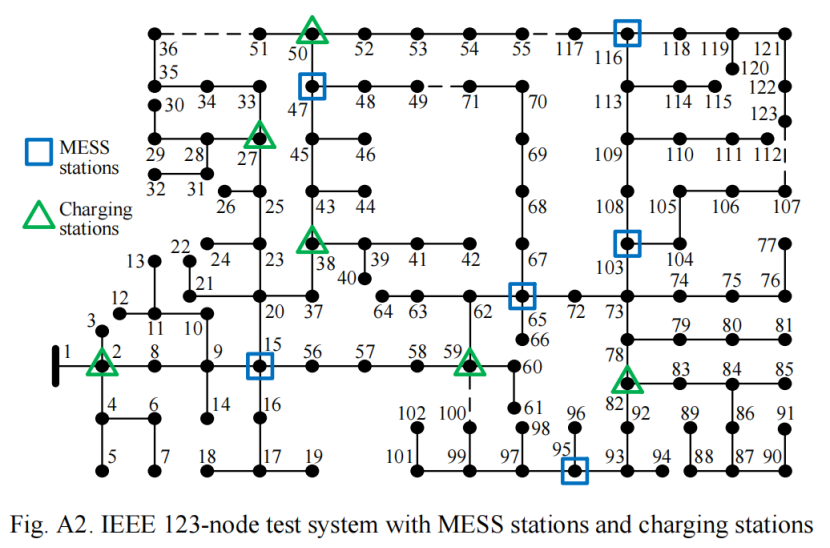
        这一步比较简单，大部分所需数据文中都已给出，部分没有提供的数据可以自己假设一下。此外，文中用到的两个配电网数据分别为IEEE 33节点配电网和IEEE 123节点配电网，数据均可从Matpower工具箱中找到，代码中将直接使用Matpower中的数据。需要注意的是，Matpower工具箱中提供的IEEE123节点配电网编号方式和原文献中有所不同，但不影响求解优化问题。

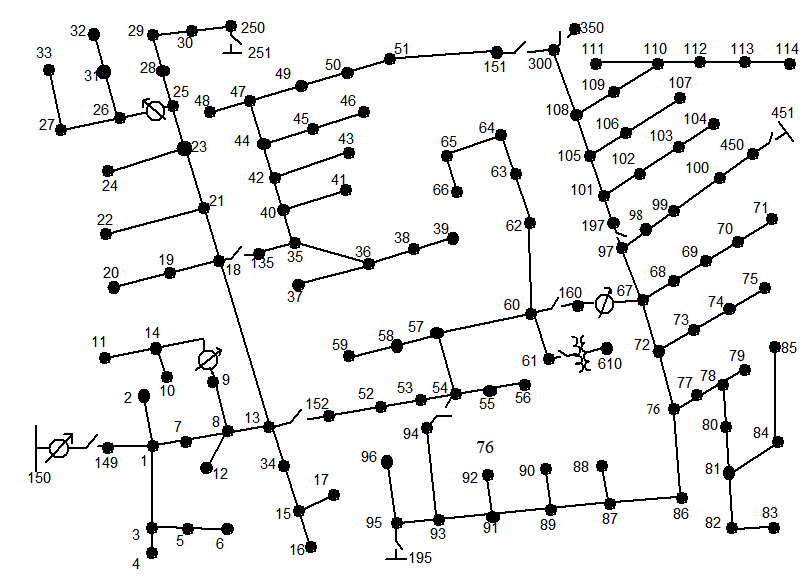
步骤2：定义第一阶段MPS预配置的决策变量

        这一步比较简单，按照表2初始化决策变量即可，同时每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。需要注意的是，EV车队、MESS和MEG的数学模型和可连接节点都是不同的，为了方便编程，可以用不同的变量进行定义。

步骤3：写第一阶段MPS预配置的目标函数和约束条件

        这一步需要按照给定的数据和定义的变量，分别写出第一阶段MPS预配置的问题的目标函数和约束条件。需要重点关注的是约束条件18，这几个约束均为非线性约束。其中约束条件18-20都包含两个0-1变量相乘的非线性项，而约束条件18还包含了功率的平方项。

        对于两个0-1变量相乘，如果需要求解确定性优化问题时，可以通过引入一个中间变量进行线性化：

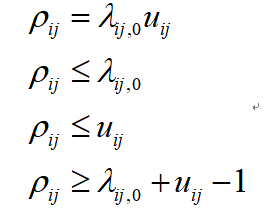
        但是，在求解两阶段鲁棒优化问题的过程中，这两个0-1变量分别在主问题和子问题中，实际上没有引入非线性项，因此无需线性化。对于包含功率平方项的约束18，可以采用圆形线性化方法，改写成如下形式：

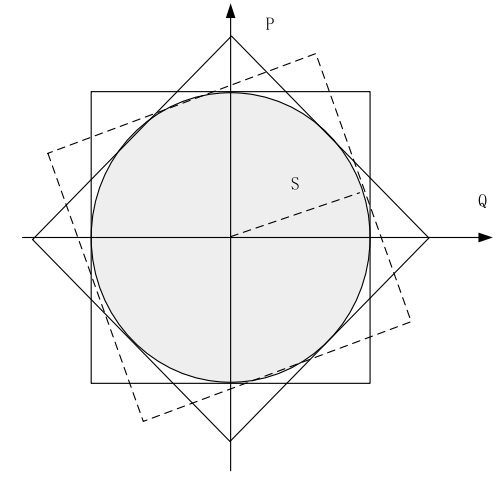
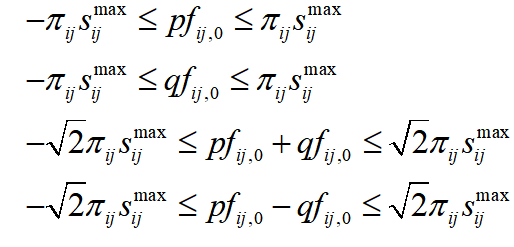
        综上，第一阶段的所有约束条件均改写成了线性的形式。

步骤4：将第一阶段优化问题改写成紧凑形式

        为了方便两阶段鲁棒优化问题的求解，需要先将上述优化问题改写成紧凑的矩阵形式，具体改写方法可以参考我之前的博客(Yalmip使用教程(6)-将约束条件写成矩阵形式-CSDN博客)

        w和z的维度一样，但z是一个常数向量，只有和有功负荷变量pi,0对应位置为负荷权重wi，其余位置均为0。

步骤5：将优化问题分为主问题和子问题，并采用对偶变换求解子问题

        主问题MP：

        原始子问题SP0为：

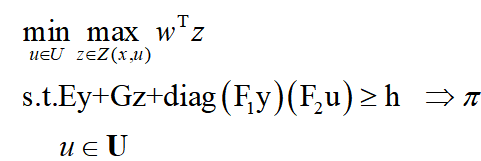
        其中，π为对偶变量，则其内层优化max问题的对偶问题可以写做：

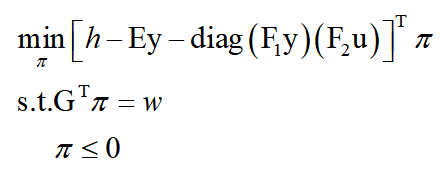
        将其与外层min问题合并得到：

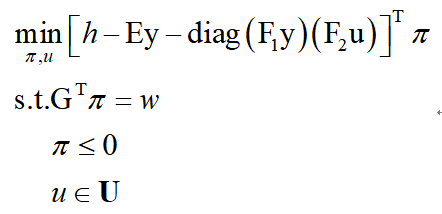
        现在子问题是一个混合整数二次规划问题，采用求解器便可以进行快速求解。但是由于问题规模比较大，求解时间可能会比较长，也可以按照原文中V-B所述方法进行线性化。

        主问题和子问题建模完成后，可以使用C&CG算法进行快速求解，具体步骤如文中V-A所述。

步骤6：使用yalmip工具箱对优化问题进行求解

        上面构建的两阶段鲁棒优化问题分为主问题和子问题，其中主问题为混合整数线性规划，子问题为混合整数二次规划，均可采用gurobi求解器进行求解。

4.Matlab代码介绍

        程序共有10个m文件和2个mat文件，其中，IEEE33.m和IEEE123.m文件为两个配电网数据文件，main33_DO.m和main123_DO.m分别为两个配电网MPS预配置问题的确定性优化模型求解的文件，main33_RO.m和main123_RO.m分别为两个配电网MPS预配置问题的两阶段鲁棒优化模型求解的文件，其中子问题采用对偶变换进行处理。Matrix33.m和Matrix123.m分别为将两个配电网MPS预配置问题转为矩阵形式的文件，show_result33.m和show_result123.m为展示两个配电网两阶段鲁棒优化运行结果的文件，Matrix33.mat和Matrix123.mat为存储的两个配电网优化问题系数矩阵。

        完整代码可从以下链接获取：

(顶刊复现)基于配电网韧性提升的应急移动电源预配置和动态调度(上)-MPS预配置matlab代码资源-CSDN文库

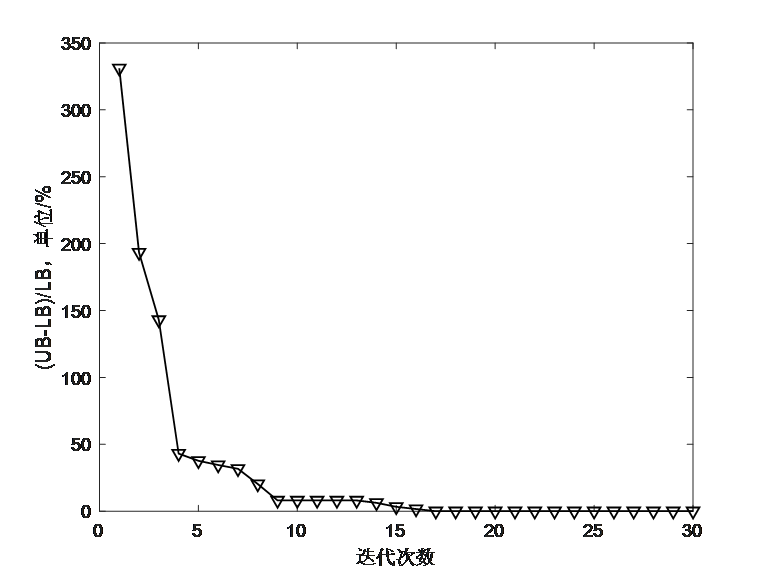
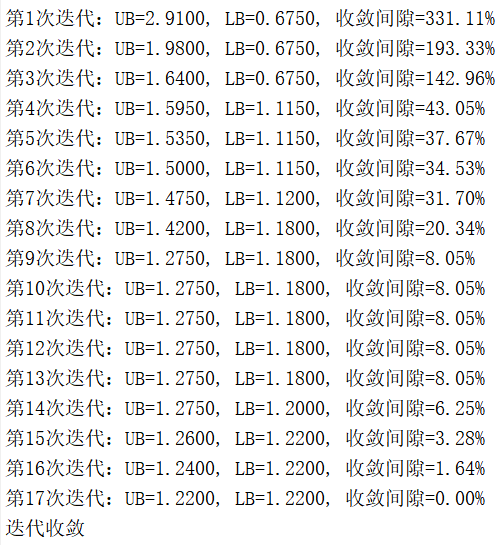
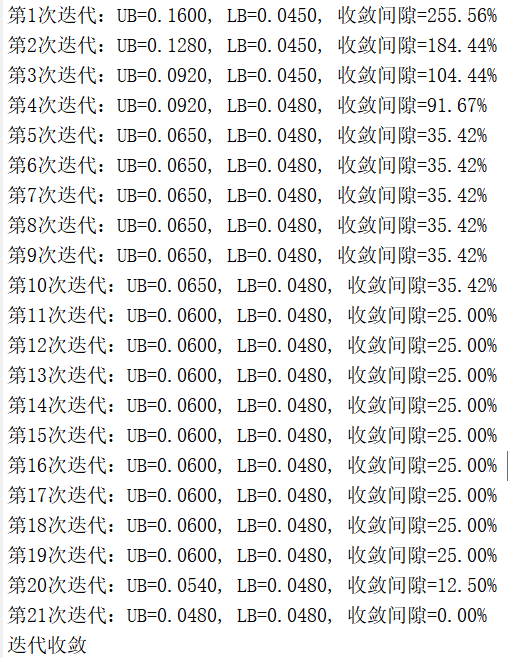
5.代码运行结果

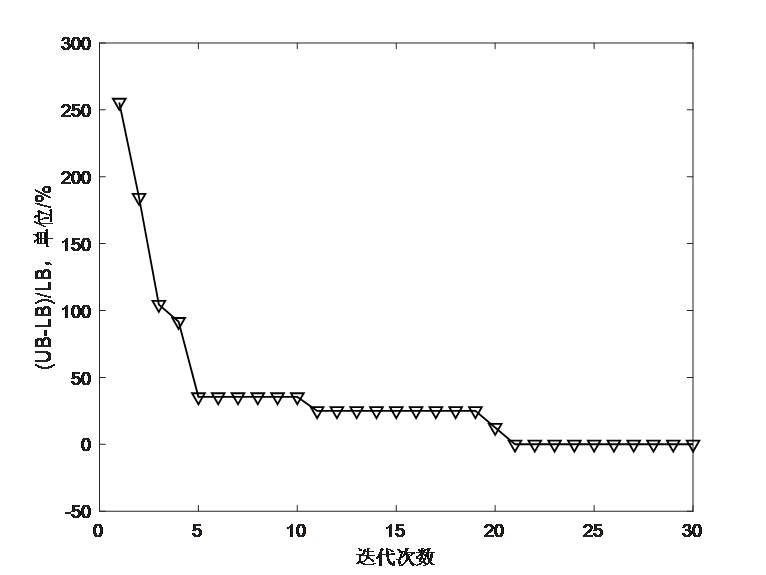
        原文中数据提供不全，所以代码复现结果和原文献相比会有偏差，但原理完全一样。

5.1 IEEE33节点优化结果

5.2 IEEE123节点优化结果