标题：【C语言】手撕二叉树

@水墨不写bug

---

正文开始：

        二叉树是一种基本的树形数据结构，对于初学者学习树形结构而言较容易接受。二叉树作为一种数据结构，在单纯存储数据方面没有  顺序表，链表，队列等线性结构  有优势，但是二叉树的搜索功能十分强大——高阶数据结构比如红黑树，B树等的基础就是搜索二叉树。

        二叉树的基本知识讲解：二叉树讲解

        对于初学者，首先学习二叉树的存储结构对于理解二叉树的本质结构非常有效。

（一）头文件

        本文不加解释的给出二叉树的头文件：

        Bitree.h

        并根据头文件来实现二叉树数据结构的相关功能。包括：二叉树的（前序）构建，二叉树的销毁，二叉树节点个数，二叉树叶子节点个数，二叉树第K层节点个数，二叉树查找值为x的节点，二叉树前序遍历，二叉树中序遍历，二叉树后序遍历，层序遍历，判断二叉树是否是完全二叉树等共11个功能。

#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<string.h>//节点数据类型
typedef char BiTreeDataType;//二叉树节点
typedef struct BiTreeNode
{BiTreeDataType _val;struct BiTreeNode* _left;struct BiTreeNode* _right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BiTreeDataType* a, int* pi);// 二叉树销毁
void BinaryTreeDestory(BTNode* root);// 二叉树节点个数
int BinaryTreeSize(BTNode* root);// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BiTreeDataType x);// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

（二）功能实现

        本文的二叉树是通过递归实现的，想要写好递归，需要注意一下几点：

        递归首先要有递归出口：

        确保递归函数的每一步都朝着基本情况靠近：在写递归函数时，确保每一步递归调用都是在缩小问题规模的基础上进行的。如果递归函数每一步都朝着基本情况靠近，那么递归一定会终止；

        写递归要有的思路：

        只考虑两层情况，即  本层递归  和  下一层递归  ，根据本层递归与下一层递归的关系，来写递归的逻辑；

        写递归要相信自己的函数：

        在写递归的时候，我们使用的下一层递归函数通常是一个黑盒，但是我们要相信递归函数一定完成任务。

（1）前序遍历

        首先判断此节点是否是空节点，若是，则退出递归。（这就是递归的出口）

        接下来访问此节点：printf（）函数的调用代表访问节点。

        最后递归访问此节点的左子树和右子树。

// 二叉树前序遍历 root + left + right
void BinaryTreePrevOrder(BTNode* root)
{//递归出口if (root == NULL)return;printf("%d", root->_val);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

（2）中序遍历

        首先判断此节点是否是空节点，若是，则退出递归。（这就是递归的出口）

        然后递归访问次节点的左子树。

        接下来访问此节点：printf（）函数的调用代表访问节点。

        最后递归访问此节点的右子树。

// 二叉树中序遍历 left + root + right
void BinaryTreeInOrder(BTNode* root)
{//递归出口if (root == NULL)return;BinaryTreePrevOrder(root->_left);printf("%d", root->_val);BinaryTreePrevOrder(root->_right);
}

（3）后序遍历

        首先判断此节点是否是空节点，若是，则退出递归。（这就是递归的出口）

        然后递归访问次节点的右子树。

        接下来访问此节点：printf（）函数的调用代表访问节点。

        最后递归访问此节点的左子树。

// 二叉树后序遍历 left + root + right
void BinaryTreePostOrder(BTNode* root)
{//递归出口if (root == NULL)return;BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%d", root->_val);
}

（4）二叉树的（前序）构建

       前序构建的思路就是前序遍历的思路：先完成对根节点的访问，再递归构建左右子树。

访问根节点：

        根据字符串的当前的字符来决定：如果当前字符为‘#’，返回NULL表示空节点；如果不是‘#’，则创建新节点，并将此字符存入新节点。

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树  pi的作用计数，便于填充数组
// 接受一个字符串，‘#’ 表示 空节点。
BTNode* BinaryTreeCreate(BiTreeDataType* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");exit(-1);}root->_val = a[(*pi)++];root->_left = BinaryTreeCreate(a,pi);root->_right = BinaryTreeCreate(a,pi);return root;
}

（5）二叉树的销毁

        递归销毁，如果此节点为空，此时不能访问此节点，直接返回即可，目的是返回到上一层来销毁；（也就是递归出口的定义）

        之后再递归销毁左子树和右子树，最后释放此节点。

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);//要在外部将root置空
}

（6）二叉树节点个数

        递归计数，如果此节点为空，返回0，不计数。

        否则返回左子树的计数结果和右子树的计数结果 + 1（此节点的计数）。

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

（7）二叉树叶子节点个数

        叶子节点有一个特征：左子树和右子树都为空。

        如果遇到这样的节点，计数+1；

        最后返回左子树与右子树的计数结果之和。

// 二叉树 叶子节点 个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left == NULL && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

（8）二叉树第K层节点个数

       模拟递归：

        想象一下：在一个楼层中，假如你要下降K层，如何计数呢？

        在这里我们需要定义一个变量k作为标牌，标识还需要下降的层数。由于本层默认标定为1，所以当k==1时，计数+1；

        最后返回递归左子树和和右子树的结果。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (NULL == root)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left,k-1) + BinaryTreeLevelKSize(root->_right,k-1);
}

（9）二叉树查找值为x的节点

         查找思路：

        首先判断根节点是否为空，若为空，表示访问到叶子节点的左右节点，返回空表示没有找到。（另一种情况根节点为空表示整棵树都为空，也返回空表示没有找到）

        如果找到x返回这个节点的地址，表示找到了。

        接下来递归访问左右子树：

        需要注意的是：

        创建一个临时变量ret_l(ret_r)来接收在左右子树查找的结果，如果找到（ret_l(ret_r)不为空）则返回左(右)子树返回的结果；

        如果左右子树都没有找到，则返回空。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BiTreeDataType x)
{if (root == NULL)return NULL;if (root->_val == x)return root;BTNode* ret_l = BinaryTreeFind(root->_left, x);if (ret_l)return ret_l;BTNode* ret_r = BinaryTreeFind(root->_right, x);if (ret_r)return ret_r;return NULL;
}

（10）层序遍历

        思路：（不使用递归，通过一个循环和数据结构队列来实现。）

        初始时进一个根节点，接下来出一进二，从队头出一个数据同时压入两个数据——出根节点的同时进左子节点和右子节点，直到把队列出为空。

        printf（）代表了对此节点的遍历。

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue queue;Qinit(&queue);if (root != NULL)Qpush(&queue, root);while (!Qempty(&queue)){BTNode* front = Qfront(&queue);//队列先进先出Qpop(&queue);printf("%d", front->_val);if (front->_left)Qpush(&queue,front->_left);if (front->_right)Qpush(&queue,front->_right);}QDestroy(&queue);
}

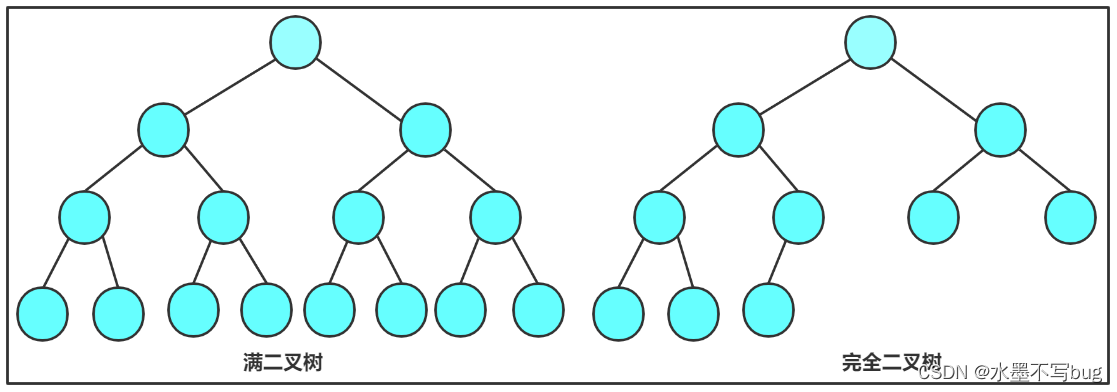
（11）判断二叉树是否是完全二叉树

       

        思路：

        通过层序遍历来遍历二叉树。完全二叉树和非完全二叉树的区别就是完全二叉树的最后一个节点之前没有空节点。通过层序遍历来遍历二叉树，当找到空节点时，此时查找队列内是否有非空节点：

        如果都是空，此树是完全二叉树；

        如果有非空节点，此树不是完全二叉树。

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue queue;Qinit(&queue);if (root != NULL)Qpush(&queue, root);while (!Qempty(&queue)){BTNode* front = Qfront(&queue);//队列先进先出Qpop(&queue);if (front == NULL)break;Qpush(&queue, front->_left);Qpush(&queue, front->_right);}//如果队列里剩下的全是NULL，则是完全二叉树；否则不是while (!Qempty(&queue)){BTNode* front = Qfront(&queue);//队列先进先出Qpop(&queue);if (front){QDestroy(&queue);return false;}}QDestroy(&queue);return true;
}

---

完~

未经作者同意禁止转载