文章目录
- 【 1. 基本原理 】
- 1.1 子树、空树
- 1.2 有序数、无序树
- 1.3 森林
- 【 2. 结点 】
- 【 3. 度、层次、深度 】
【 1. 基本原理 】
- 树结构是一种 非线性存储结构,存储的是具有 一对多 关系的数据元素的集合。
- 一对多
如下图中的左图所示,对于数据 A 来说,和数据 B、C、D 有关系;对于数据 B 来说,和 E、F 有关系。这就是“一对多”的关系。
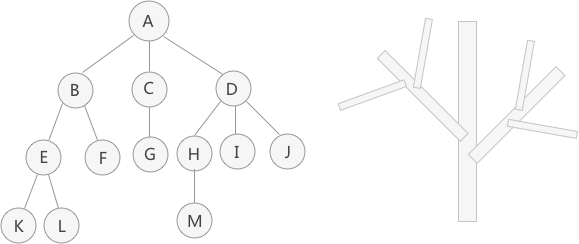
- 将具有“一对多”关系的集合中的数据元素按照上面右图的形式进行存储,整个存储形状在逻辑结构上看,类似于实际生活中倒着的树(左图倒过来),所以称这种存储结构为 树型存储结构。
- 树的广义表 表示法
上图用广义表可以表示为:
(A , ( B ( E ( K , L ) , F ) , C ( G ) , D ( H ( M ) , I , J ) ) )
1.1 子树、空树
- 子树:上图中,整棵树的根结点为结点 A,而如果单看结点 B、E、F、K、L 组成的部分来说,也是棵树,而且节点 B 为这棵树的根结点。所以称 B、E、F、K、L 这几个结点组成的树为整棵树的子树;同样,结点 E、K、L 构成的也是一棵子树,根结点为 E。
单个结点也是一棵树,根结点就是它本身。上图中的结点 K、L、F 等都是树,且都是整棵树的子树。
知道了子树的概念后,树可以这样定义:树是由根结点和若干棵子树构成的。 - 在树结构中, 对于具有同一个根结点的各个子树,相互之间不能有交集。
例如上图中,除了根结点 A,其余元素又各自构成了三个子树,根结点分别为 B、C、D,这三个子树相互之间没有相同的结点。如果有,就破坏了树的结构,不能算做是一棵树。 - 空树:如果集合本身为空,那么构成的树就被称为空树。 空树中没有结点。
1.2 有序数、无序树
- 如果树中结点的子树从左到右看,谁在左边,谁在右边,是有规定的,这棵树称为 有序树;反之称为 无序树。
在有序树中,一个结点最左边的子树称为 第一个孩子 ,最右边的称为 最后一个孩子 。
例如上图中,如果其本身是一棵有序树,则以结点 B 为根结点的子树为整棵树的第一个孩子,以结点 D 为根结点的子树为整棵树的最后一个孩子。
1.3 森林
- 由 m(m >= 0)个互不相交的树组成的集合被称为 森林 。例如上图中,分别以 B、C、D 为根结点的三棵子树就可以称为森林。
- 前面讲到,树可以理解为是由根结点和若干子树构成的,而这若干子树本身是一个森林,所以,树还可以理解为是由根结点和森林组成的。用一个式子表示为:
Tree =(root,F),其中,root 表示树的根结点,F 表示由 m(m >= 0)棵树组成的森林。
除了上图表示树的方法外,还有其他表示方法:
【 2. 结点 】
- 结点:使用树结构存储的每一个数据元素都被称为结点。例如,上图中的数据元素 A 就是一个结点;
- 父结点(双亲结点)、子结点 、兄弟结点:
对于上图中的结点 A、B、C、D 来说,A 是 B、C、D 结点的父结点(也称为“双亲结点”);B、C、D 都是 A 结点的子结点(也称“孩子结点”);
对于 B、C、D 来说,它们都有相同的父结点,所以它们互为兄弟结点。 - 树根结点(根结点):每一个非空树都有且只有一个被称为根的结点。上图中的结点 A 就是整棵树的根结点。
树根的判断依据为: 如果一个结点没有父结点,那么这个结点就是整棵树的根结点 。 - 叶子结点:如果结点没有任何子结点,那么此结点称为叶子结点(叶结点)。例如上图中,结点 K、L、F、G、M、I、J 都是这棵树的叶子结点。
【 3. 度、层次、深度 】
- 对于一个结点, 拥有的子树的数量(结点有多少分支)称为结点的 度(Degree)。例如上图中,根结点 A 下分出了 3 个子树,所以,结点 A 的度为 3。
一棵树的度 是树内各结点的度的最大值。例如上图中,各个结点的度的最大值为 3,所以,整棵树的度的值是 3。 - 结点的层次:从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层,依次类推。例如上图中,A 结点在第一层,B、C、D 为第二层,E、F、G、H、I、J 在第三层,K、L、M 在第四层。
- 一棵树的 深度(高度)是树中结点所在的最大的层次。例如上图中树的深度为 4。
- 如果两个结点的父结点虽不相同,但是它们的父结点处在同一层次上,那么这两个结点互为 堂兄弟。例如上图中,结点 G 和 E、F、H、I、J 的父结点都在第二层,所以之间为堂兄弟的关系。