AVLTree
- 1、树的分类
- 2、平衡二叉树
- 2.1、构建一个平衡二叉树
- 2.2、删除节点
- 2.3、搜索方式
- 2.3.1、广度优先搜索(BFS)
- 2.3.2、深度优先搜索(DFS)
1、树的分类
树形结构是编程当中特别常见的一种数据结构。比如电脑中的文件管理系统就大量用到树结构。

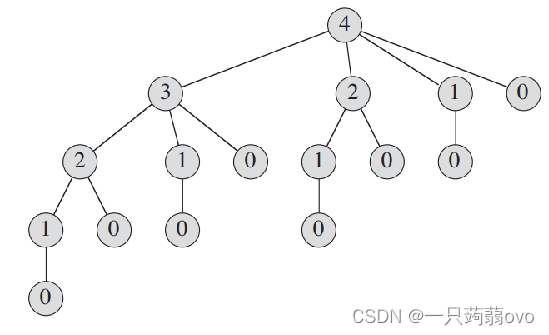
该图取之于这篇文章 硬核总结!真二叉树、满二叉树、完全二叉树的性质与概念,这篇文章对一些基础的树总结的很好。所以我也不赘诉了。
2、平衡二叉树
平衡二叉树的基础是二叉搜索树,对于一个二叉搜索树而言,新插入的数字若小于根节点则放在左边,反之放在右边。但如果插入的数字一直小于或大于根节点,那这个树,就和链表差不多了。如图,我按顺序插入(1, 0, 3, 2, 4, 5, 6)。

本来二叉树的实现就是为了减低搜索的时间复杂度的,而如果树构建得和单链表差不多,那便失去了意义。所以二叉平衡搜索树,又称平衡二叉树应运而生。
平衡二叉树要求左子树的高度和右子树的高度之不能超过1。
2.1、构建一个平衡二叉树
正如前面所言,一个平衡二叉树,首先得是一个二叉搜索树,然后再要求左右子树高度差不超一。于是人们总结出四种会导致不平衡的情况。
1、LL型:即左子树的左子树增高了一层,从而导致不平衡。

上图是一个简单的模型,实际上为了解决不平衡的问题,要解决的事情远不止怎么简单。下面是一个更为通用的模型。我不仅需要把a变成b的右子树,还需要把原来b的右子树变成a的左子树,然后还要让原来指向a的指针指向b。这是一个颇为麻烦的事情,最难的部分是要改变根节点上级指针。

2、LR型:左子树的右子树添加了一层导致不平衡。直接上图。

另外两种类型就是RR和RL了,逻辑和上述两种都是一样的。再写代码的时候甚至可以把所以left和right调换然后就可以实现LL到RR的转换或LR到RL的转换。而我懒得画图就不再画了。
直接上代码。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define n 9struct Node
{int data;Node* right;Node* left;Node() {};Node(int x): data(x) {}; //constructor
};class AVLTree
{
public:Node* root;AVLTree(){root = nullptr;};int get_height(Node* node);void append_data(Node** node, int num); //append a number into the AVL treevoid rrRotation(Node** root);void rlRotation(Node** root);void llRotation(Node** root);void lrRotation(Node** root);
};int AVLTree::get_height(Node* node)
{if(node == nullptr) return 0;return max(get_height(node->left), get_height(node->right)) + 1;
}void AVLTree::append_data(Node** node, int data)
{if(*node == nullptr){*node = new Node(data);(*node)->right = nullptr;(*node)->left = nullptr;}else if(data < (*node)->data){append_data(&(*node)->left, data);if(abs(get_height((*node)->right) - get_height((*node)->left)) > 1){if(data < (*node)->left->data) llRotation(node);else lrRotation(node);}}else{append_data(&(*node)->right, data);if(abs(get_height((*node)->right) - get_height((*node)->left)) > 1){if(data > (*node)->right->data) rrRotation(node);else rlRotation(node);}}
}void AVLTree::llRotation(Node** root)
{Node* temp = (*root)->left;(*root)->left = temp->right;temp->right = *root;*root = temp;
}void AVLTree::lrRotation(Node** root)
{Node* temp = (*root)->left->right;(*root)->left->right = temp->left;temp->right = *root;Node* temp2 = temp->left;temp->left = (*root)->left;(*root)->left = temp2;*root = temp;
}void AVLTree::rrRotation(Node** root)
{Node* temp = (*root)->right;(*root)->right = temp->left;temp->left = *root;*root = temp;
}void AVLTree::rlRotation(Node** root)
{Node* temp = (*root)->right->left;(*root)->right->left = temp->right;temp->left = *root;Node* temp2 = temp->right;temp->right = (*root)->right;(*root)->right = temp2;*root = temp;
}int randomArray[n] = {16, 3, 7, 11, 9, 26, 18, 14, 15};int main()
{class AVLTree mytree;for(int i = 0; i < n; i++)mytree.append_data(&mytree.root, randomArray[i]);printf("the height of tree is: %d\n", mytree.get_height(mytree.root));system("pause");return 0;
}
在这个代码实现中,最令我头疼的是二级指针这里。我一开始不太明白用二级指针的意义,然后尝试了许多次才不得不使用它。
因为在我插入一个节点之后,我是通过反向遍历的方式去查找哪个节点失衡了。但是此时有一个问题,当我得知这个节点失衡之后,我并不清楚它的上一个节点再哪里,因此我无法改变上一个节点所存储的指针。有点绕,我画个图。
如下面两个图所示,如果b这个节点失衡了,但又因为我用的是反向遍历,所以我并不知道a这个节点的地址。故而我无法改变a->right的指向。而为了解决这个问题,我不得不引入二级指针,让我得到b的地址的同时,也得知a.right的地址。


具体逻辑是任何对b的操作,都是先取得&a.right再解引用。这样相当于知道b便知道a.right的地址。

以上,如果不动手实践的话,大概是看不明白的。。。
2.2、删除节点
下面这个图表红的三个框,分别对应着删除一个节点的三种情况。
情况一:节点位于末端,直接删除即可;
情况二:节点有一个孩子,那么删除之后需要重新建立起父子连接;
情况三:节点有两个孩子,此时有两种策略。第一种策略是把右孩子,即右子树的最小值复制到自己身上。然后把被复制的那个节点删除。第二种策略是把左子树的最大值复制到自己身上,然后把被复制的那个节点删除。

下面这个图是遇到情况三之后采取策略一的示意图。看到这里,可能许多人还存在一个疑惑,难道不怕2下面还有孩子吗?答案是否定的,因为右子树的最小值,即为最值,自然就是没有孩子的节点了。所以此时删除2,只需要切换到情况一即可。

2.3、搜索方式
2.3.1、广度优先搜索(BFS)
如图,广度优先搜索是从根节点到末节点,一层一层这些遍历下去的。实现起来也并不复杂,只需要设置一个FIFO容器,比如queue。不断的从容器中读取节点即可。

queue内部的示意图大概是这样,但要注意,其实这些值不会同时出现在queue当中。

代码实现如下:
void bfs(Node** root)
{Node* temp = nullptr;queue<Node*> Q;if(*root != nullptr) Q.push(*root);else return;while(!Q.empty()){temp = Q.front();if(temp->left != nullptr) Q.push(temp->left);if(temp->right != nullptr) Q.push(temp->right);cout << temp->data << endl;···Q.pop();}
}
2.3.2、深度优先搜索(DFS)
深度优先搜索分为前序遍历、中序遍历和后序遍历。主要还是依靠递归来实现。在代码上只是改动输出值的位置,相对容易。
void dfs_preorder(Node** node) //前序
{if(*node == nullptr) return;cout << (*node)->data << endl;dfs_preorder(&((*node)->left));dfs_preorder(&((*node)->right));
}void dfs_inorder(Node** node) //中序
{if(*node == nullptr) return;dfs_preorder(&((*node)->left));cout << (*node)->data << endl;dfs_preorder(&((*node)->right));
}void dfs_postorder(Node** node) //后序
{if(*node == nullptr) return;dfs_preorder(&((*node)->left));dfs_preorder(&((*node)->right));cout << (*node)->data << endl;
}
分别看一下前序、中序、后序的打印顺序吧。注意,在以下这些图中,节点中的数字代表的是打印顺序。