A题 多个火箭残骸的准确定位
问题1 :建立数学模型,分析如果要精准确定空中单个残骸发生音爆时的位置坐标(经度、纬度、高程)和时间,至少需要布置几台监测设备?假设某火箭一级残骸分离后,在落点附近布置了7台监测设备,各台设备三维坐标(经度、纬度、高程)、音爆抵达时间(相对于观测系统时钟0时)如下表所示:
思路1:
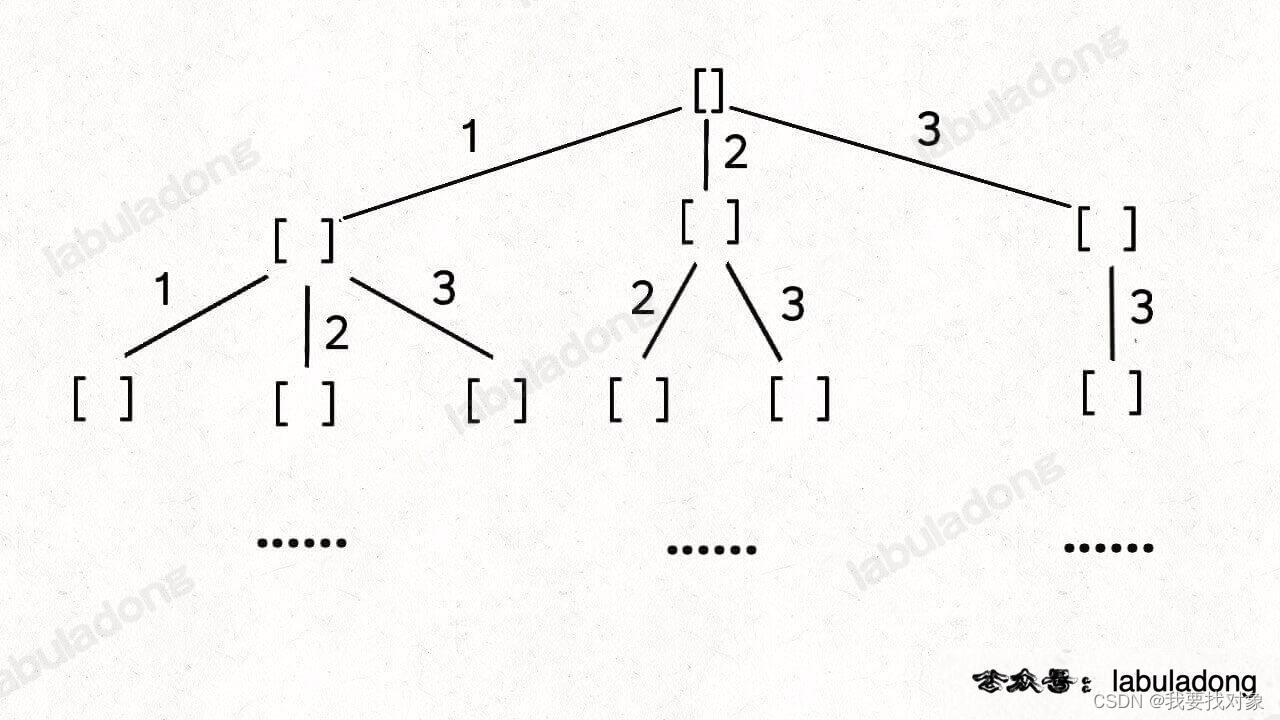
可以采用多边测量方法,根据不同监测设备接收到的音爆抵达时间来确定音爆的发生位置和时间。这个方法基于声速在空气中的传播速度和声波到达不同监测设备的时间差来确定源的位置。
step1:建立问题模型
日标是确定火箭残骸音爆发生的精确位置(经度、纬度、高程)和时间。这需要解决四个未知数音爆的经度 lon,纬度lat,高程z,以及音爆发生的时间 t。
step2:数据准备
有七个监测设备,每个设备记录了音爆到达的时间,以及它们的经纬度和高程。震动波的传播速度为340 m/s,
step3:计算音爆点到第i个设备的距离
经典的模型如半正矢公式,或者直接按题目的假设,计算两点间距离时可忽略地面曲率,纬度间每度距离值近似为111.263 km,经度间每度距离值近似为97.304 km。

step4:定义目标函数
定义一个目标函数来最小化残骸音爆后抵达7个监测设备预测时间和实际测量时间之间的平方差。这个目标函数基于预测的距离除以以声速得到的传播时间,也就是前面我们通过步骤1随机设置一组音爆点初始位置,进而可以计算得到这组初始位置距离各个监测设备的音爆到达时间,对比与真实音爆到达时间的平方差

其中,Si是从音爆点到第之个设备的距离,t 是音爆发生的时间,ti是第i个设备接收到音爆的时间,c是振动波速度。
第五步:优化求解
使用数值优化方法(例如 Nelder-Mead 算法、遗传算法、pso、梯度下降法等等)求解上述目标函数,找到最佳的 lon,lat,z,和 to值,使目标函数值最小。
这一问的优化点有2个:1是距离求解公式(可以采用精度更高的经纬度换算公式);2是规划求解的方式(可以采用启发式算法)
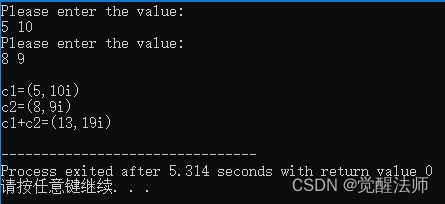
这里我已经实现,下图是直接按题目的假设的结果
即计算两点间距离时可忽略地面曲率,纬度间每度距离值近似为111.263 km,经度间每度距离值近似为97.304 km。

下图是采用半正矢公式求解后的结果

问题2 火箭残骸除了一级残骸,还有两个或者四个助推器。在多个残骸发生音爆时,监测设备在监测范围内可能会采集到几组音爆数据。假设空中有4个残骸,每个设备按照时间先后顺序收到4组震动波。建立数学模型,分析如何确定监测设备接收到的震动波是来自哪一个残骸?如果要确定4个残骸在空中发生音爆时的位置和时间,至少需要布置多少台监测设备?
思路2:
在问题的基础上,增加三组未知数,也就是一共四组参数的最小化残骸音爆后抵达7个监测设备预测时间和实际测量时间之间的平方差

从数学角度来看,只需要4个监测设备即可,当然更多也可以,这里要求不能4个监测设备在同一直线上
问题3 假设各台监测设备布置的坐标和4个音爆抵达时间分别如下表所示:利用问题2所建立的数学模型,从上表中选取合适的数据,确定4个残骸在空中发生音爆时的位置和时间(4个残骸产生音爆的时间可能不同,但互相差别不超过5 s)。
| 设备 | 经度(°) | 纬度(°) | 高程(m) | 音爆抵达时间(s) | |||
| A | 110.241 | 27.204 | 824 | 100.767 | 164.229 | 214.850 | 270.065 |
| B | 110.783 | 27.456 | 727 | 92.453 | 112.220 | 169.362 | 196.583 |
| C | 110.762 | 27.785 | 742 | 75.560 | 110.696 | 156.936 | 188.020 |
| D | 110.251 | 28.025 | 850 | 94.653 | 141.409 | 196.517 | 258.985 |
| E | 110.524 | 27.617 | 786 | 78.600 | 86.216 | 118.443 | 126.669 |
| F | 110.467 | 28.081 | 678 | 67.274 | 166.270 | 175.482 | 266.871 |
| G | 110.047 | 27.521 | 575 | 103.738 | 163.024 | 206.789 | 210.306 |
代入问题2进行求解即可
问题4 假设设备记录时间存在0.5 s的随机误差,请修正问题2所建立的模型以较精确地确定4个残骸在空中发生音爆时的位置和时间。通过对问题3表中数据叠加随机误差,给出修正模型的算例,并分析结果误差。如果时间误差无法降低,提供一种解决方案实现残骸空中的精准定位(误差<km),并自行根据问题3所计算得到的定位结果模拟所需的监测设备位置和音爆抵达时间数据,验证相关模型。
针对黄色部分的问题,可以通过模拟随机误差后的数据,求位置均值来进行调整,也就是往各组音爆抵达时间(s)加入随机数,模拟个几十组或几百组,重新求解四个残骸在空中发生音爆时的位置和时间,看看与没加入误差前的差异是否明显,可以用单样本T检验来证明,分析差异。
针对绿色部分的问题,同样是往各组音爆抵达时间(s)加入随机数,模拟个几十组或几百组,然后建立4个回归模型,用于预测发生音爆时的位置和时间,然后要求通过换算评价指标设置要求误差<km,具体做法可以参考我视频讲解,
2024东三省深圳杯A题保姆解题思路及代码 多个火箭残骸的准确定位_哔哩哔哩_bilibiliwww.bilibili.com/video/BV1Vr42137gW/?spm_id_from=333.999.0.0编辑