这里写目录标题
- 1 回溯
- 1.1 思路及模板
- 1.1 plus 排列组合子集问题
- 1.2 例题
- 1.2.1 全排列
- 1.2.2 N 皇后
- 1.2.3 N皇后问题 II
- 1.2.4 子集 (子集/排列问题)
- 1.2.4 组合(组合/子集问题)
- 1.2.5 全排列 (排列问题)1.2.1做过
- 1.2.6 子集II (可重复元素的组合/子集)
- 1.2.7 排列组合II
- 1.2.7 全排列 II (排列题型)
- 1.2.8 组合总和 (子集/组合(元素无重可复选))
- 1.2.9 排列(元素无重可复选)
1 回溯
1.1 思路及模板
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。‘
站在回溯树的一个节点上,你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法的框架如下:
result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择
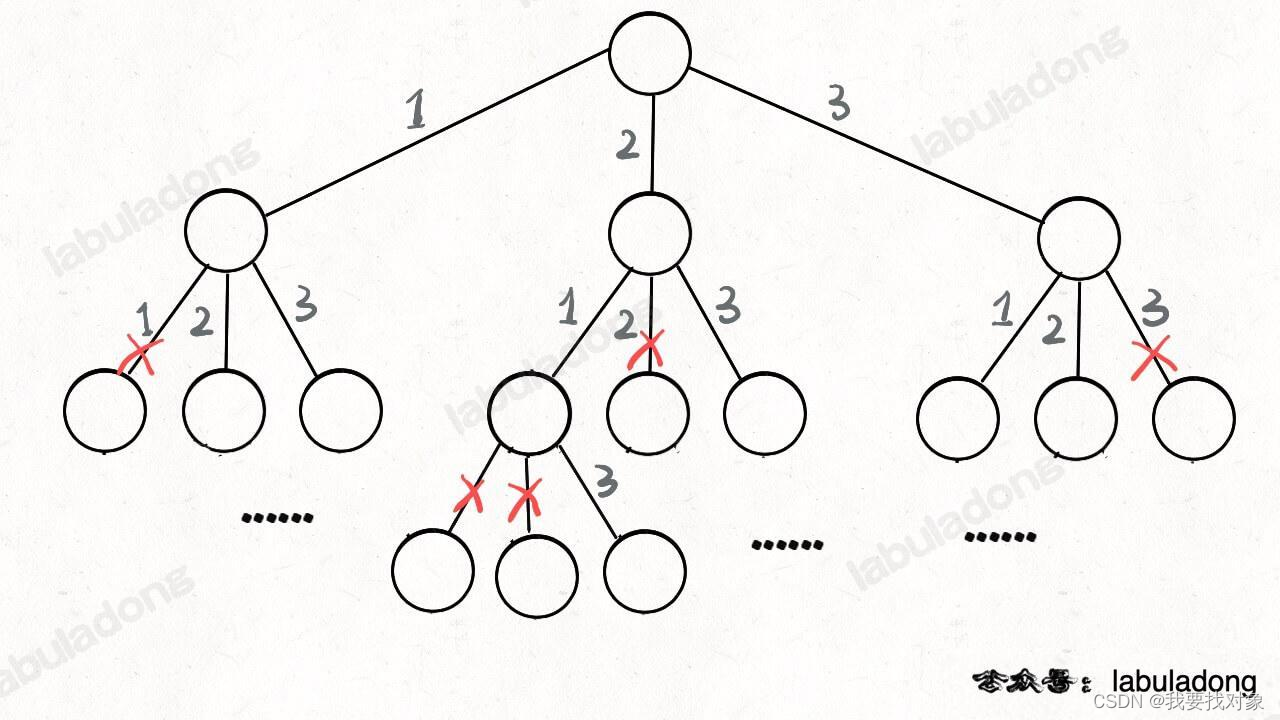
更具体的,在下面的例子中,对于遍历到红色节点来说,现在可以解答开头的几个名词:[2] 就是「路径」,记录你已经做过的选择;[1,3] 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层叶子节点,这里也就是选择列表为空的时候。
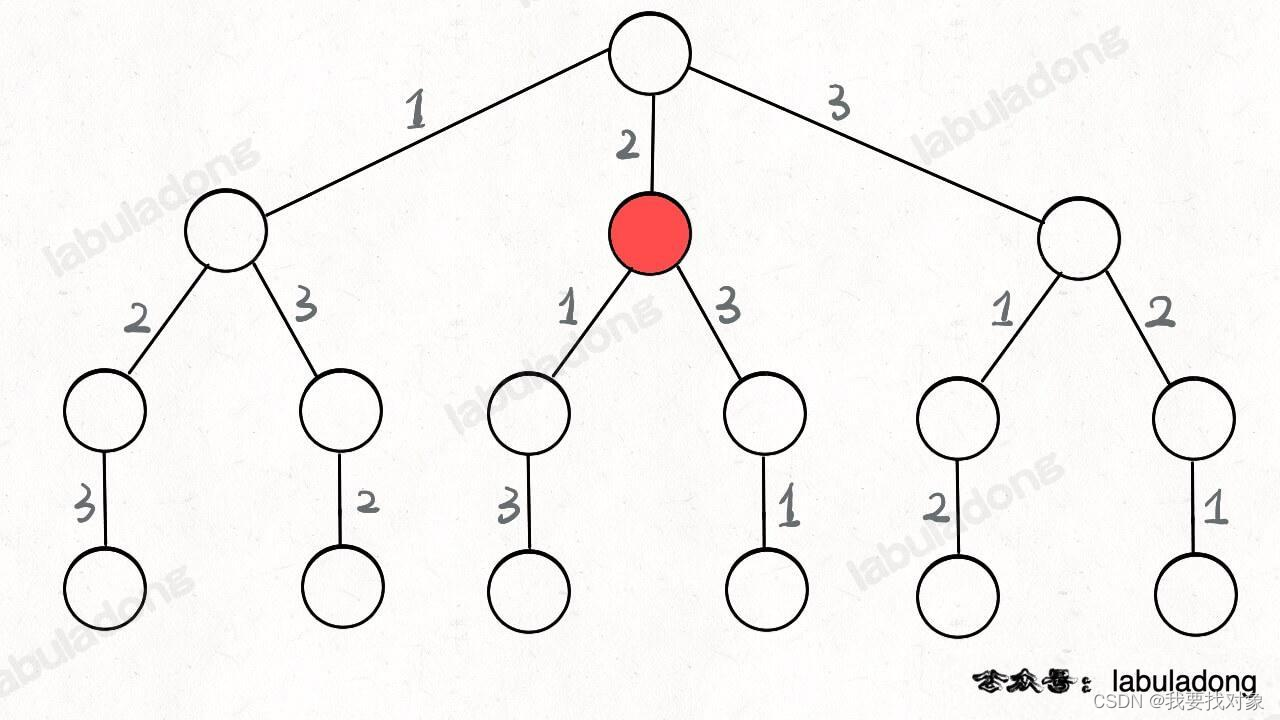
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个蓝色节点的属性:
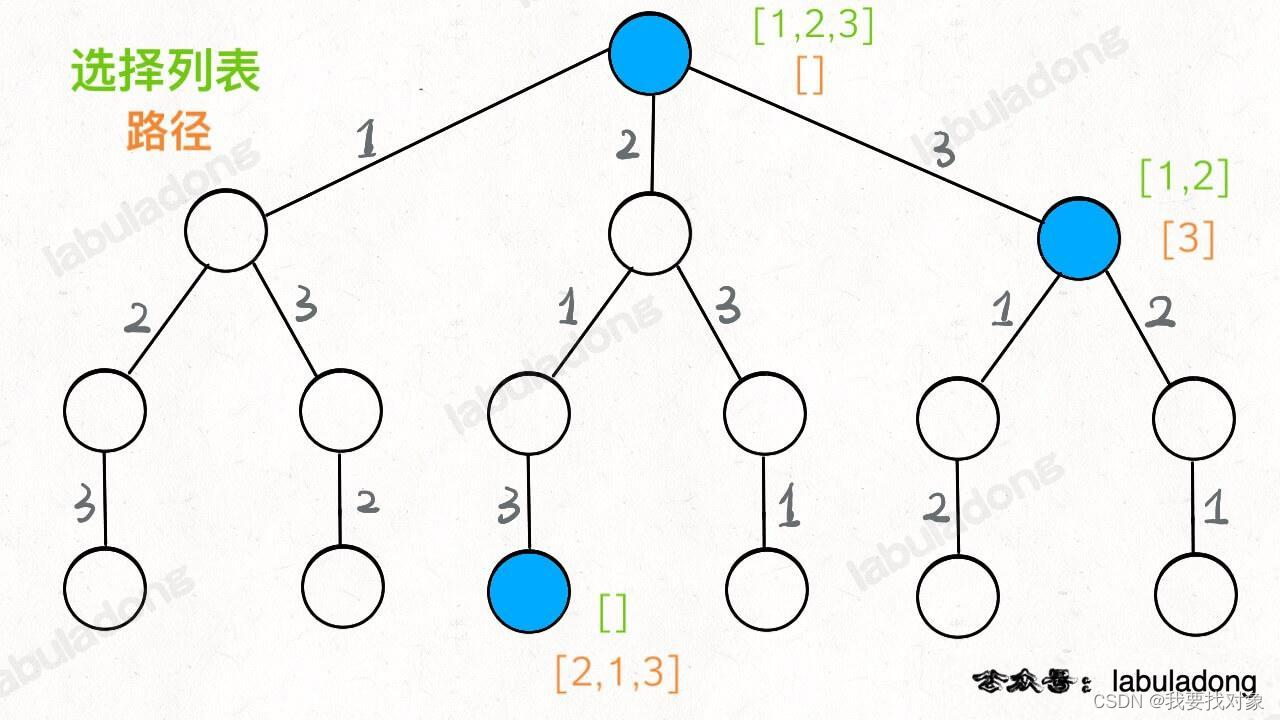
函数在树上游走要正确处理节点的属性,那么就要在这两个特殊时间点搞点动作:
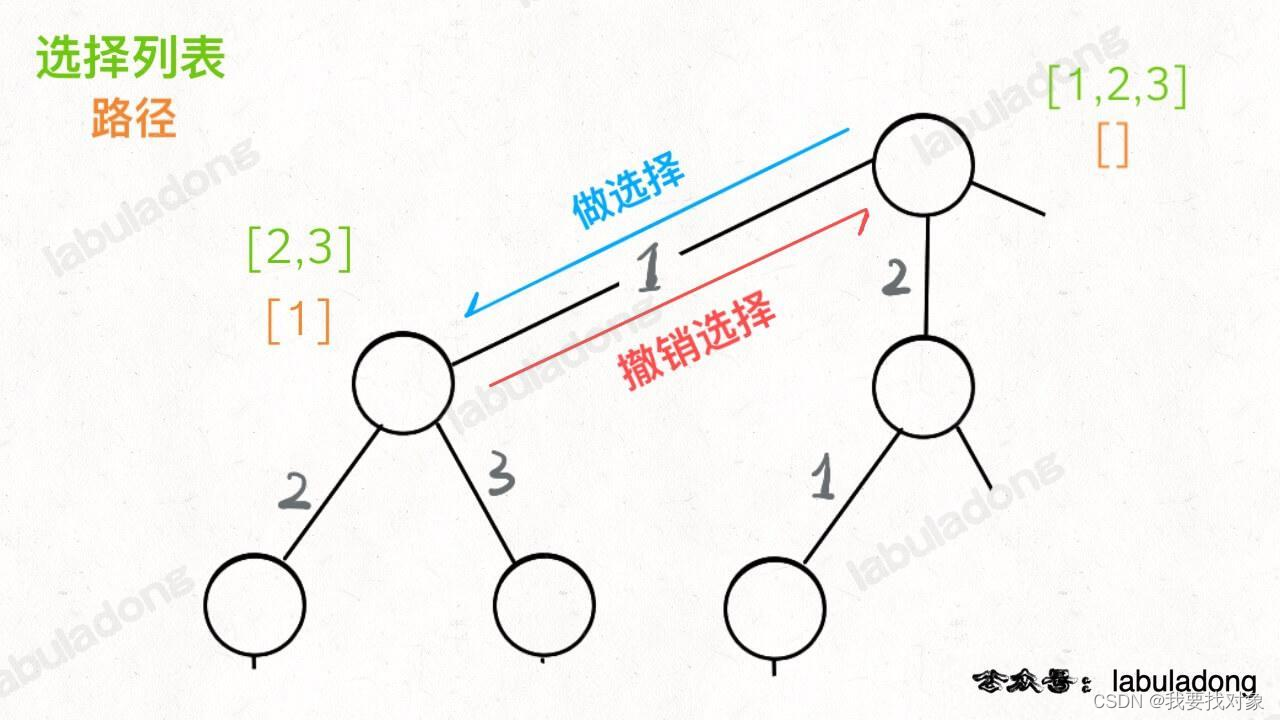
再来理解下回溯框架:
for 选择 in 选择列表:# 做选择将该选择从选择列表移除路径.add(选择)backtrack(路径, 选择列表)# 撤销选择路径.remove(选择)将该选择再加入选择列表
1.1 plus 排列组合子集问题
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素
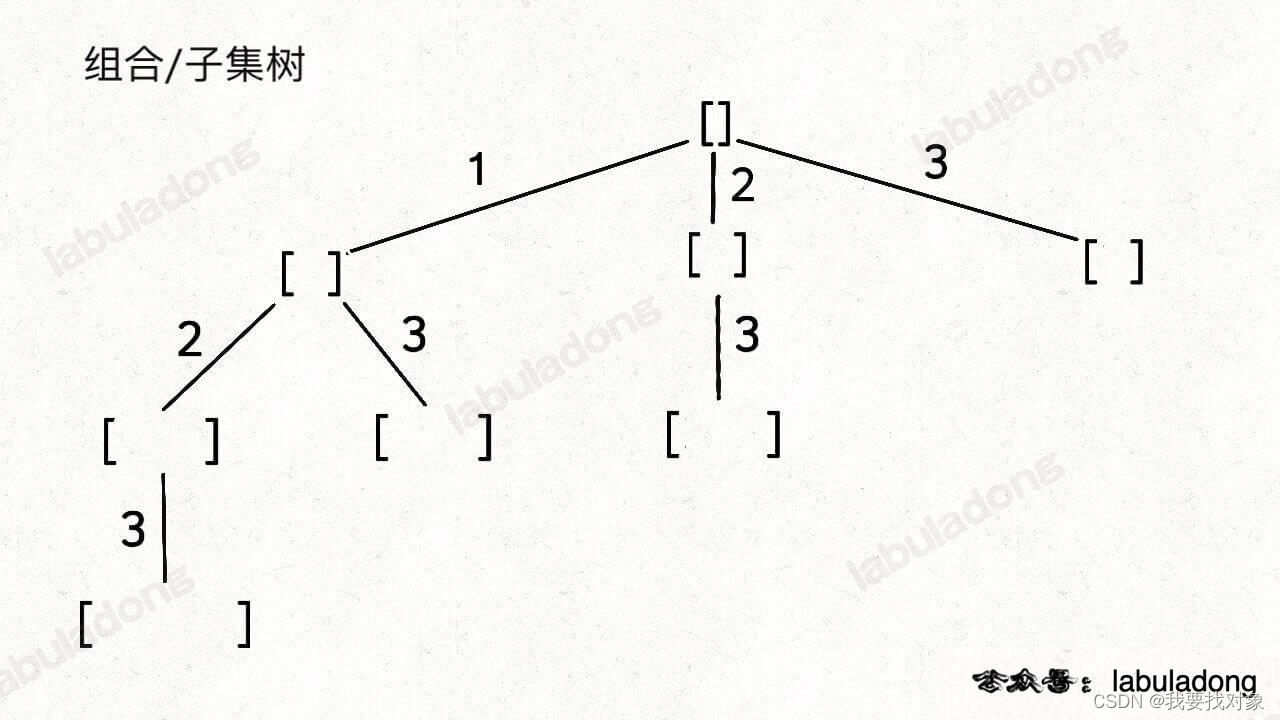
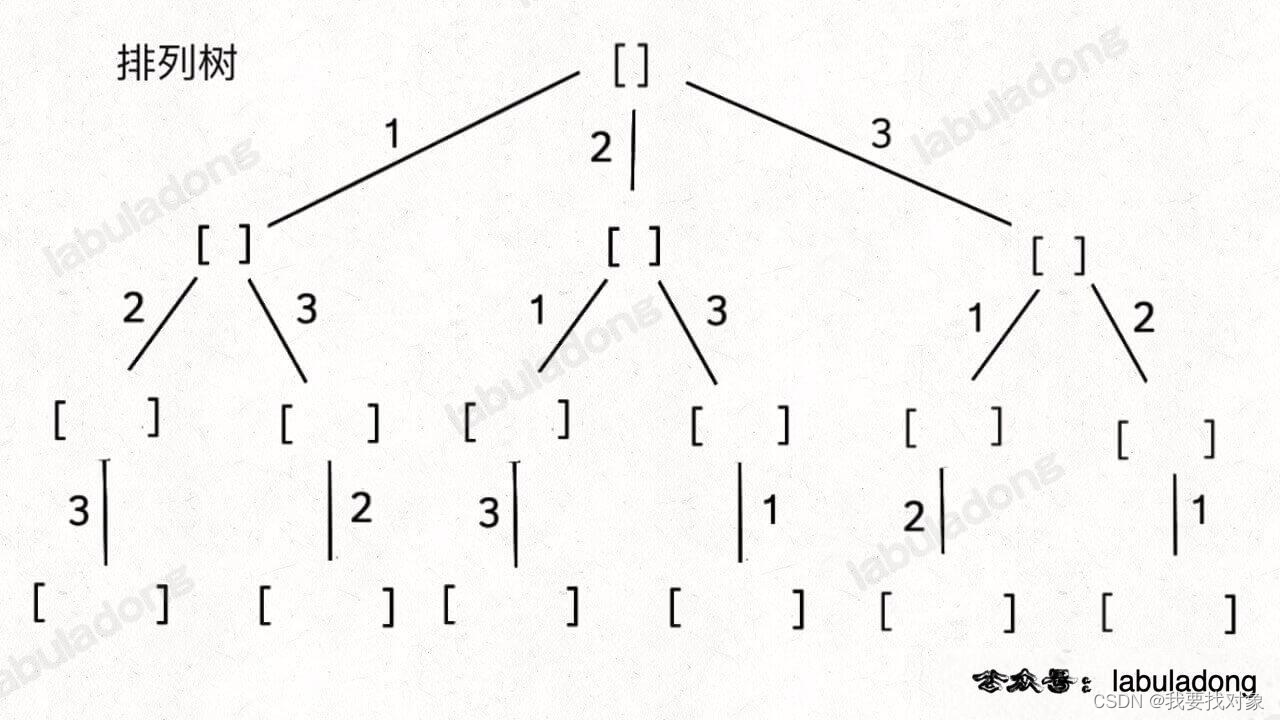
1.2 例题
1.2.1 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
思路以及代码
1、路径:走过的记录在track中。
2、选择列表:used[] 为false表示没走过,可以选择。
3、结束条件:track.size == nums.length 表示到达了叶子节点,可以退出。
class Solution {//存放结果List<List<Integer>> res = new LinkedList();public List<List<Integer>> permute(int[] nums) {List<Integer> track = new LinkedList();boolean[] used = new boolean[nums.length];backtrack(nums,track,used);return res;}// 路径:记录在 track 中// 选择列表:nums 中不存在于 track 的那些元素(used[i] 为 false)// 结束条件:nums 中的元素全都在 track 中出现public void backtrack(int[] nums,List<Integer> track,boolean[] used){//当该条路径的track和nums元素相同,也就是已经走到了叶子节点,退出if(track.size() == nums.length){res.add(new LinkedList(track));return ;}for(int i = 0;i<nums.length;i++){//排除不合法if(used[i]){continue;}//做选择track.add(nums[i]);used[i] = true;//进入下一层决策树backtrack(nums,track,used);//退出track.removeLast();used[i] = false;}}
}
1.2.2 N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
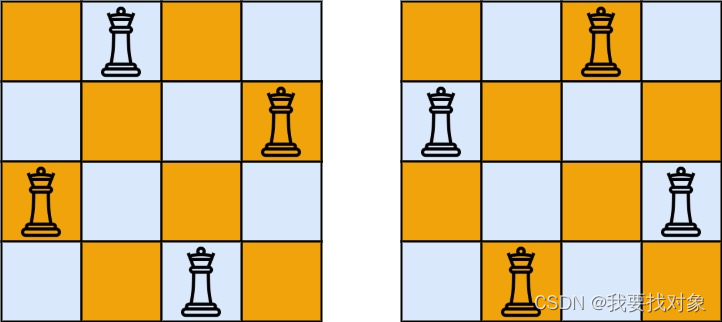
输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
思路以及代码:
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
路径:board中小于row的行都已经放置了Q
选择列表:board中第row行的所有列都可以选择
结束条件:当超过了最后一行,也就是row = board.size()
class Solution {
public://存放结果vector<vector<string>> res;vector<vector<string>> solveNQueens(int n) {// vector<string> 代表一个棋盘// '.' 表示空,'Q' 表示皇后,初始化空棋盘vector<string> board(n, string(n, '.'));backtrack(board, 0);return res;}//路径:board中小于row的行都已经放置了Q//选择列表:board中第row行的所有列都可以选择//结束条件:当超过了最后一行,也就是row = board.size()void backtrack(vector<string>& board,int row){if(board.size() == row){res.push_back(board);return;}int n = board[row].size();for(int col = 0;col<n;col++){// 排除不合法选择if (!isValid(board, row, col)) {continue;}// 做选择board[row][col] = 'Q';// 进入下一行决策backtrack(board, row + 1);// 撤销选择board[row][col] = '.';}}//输入棋盘board,判断第row行的第col列是否可以放Q?bool isValid(vector<string> board,int row,int col){int n = board.size();//检查同一列是否有冲突for(int i = 0;i<=row;i++){if(board[i][col] == 'Q'){return false;}}//检查右上for(int i = row - 1,j = col + 1;i >= 0 && j < n;i--,j++){if(board[i][j] == 'Q'){return false;}}//检查左上for(int i = row - 1,j = col - 1;i>=0 && j>=0;i--,j--){if(board[i][j] == 'Q'){return false;}}return true;}
};
1.2.3 N皇后问题 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
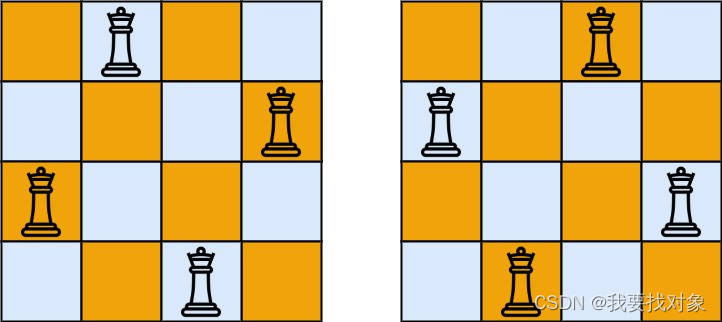
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
思路以及代码:
这道题和N皇后几乎一样,只需要将N皇后的退出返回数组改为退出res++即可,如下所示:
if(board.size() == row){res++;return;}
1.2.4 子集 (子集/排列问题)
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
思路以及代码:
这其实是一个小学问题,nums = [1,2,3],那么怎么获取它的子集?
首先考虑空集[],接着在空集的基础上衍生出一个元素的子集:
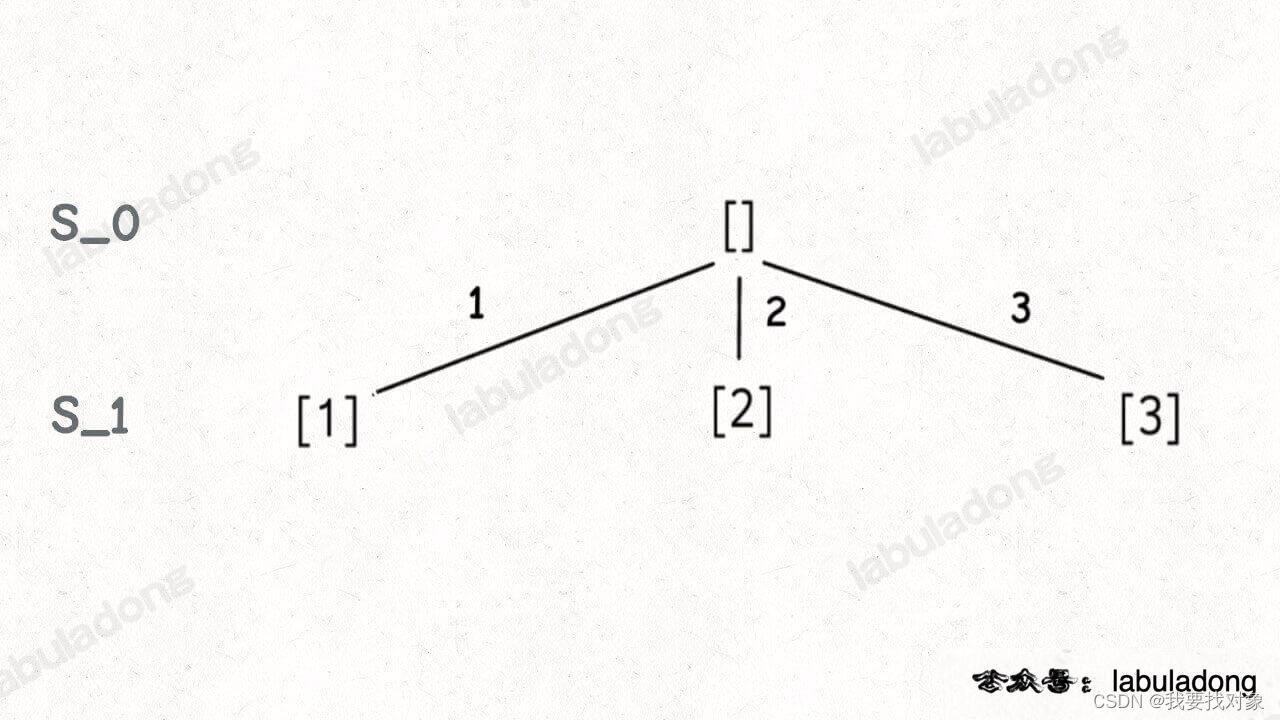
再接着,再[1],[2]上衍生出两个元素的子集:
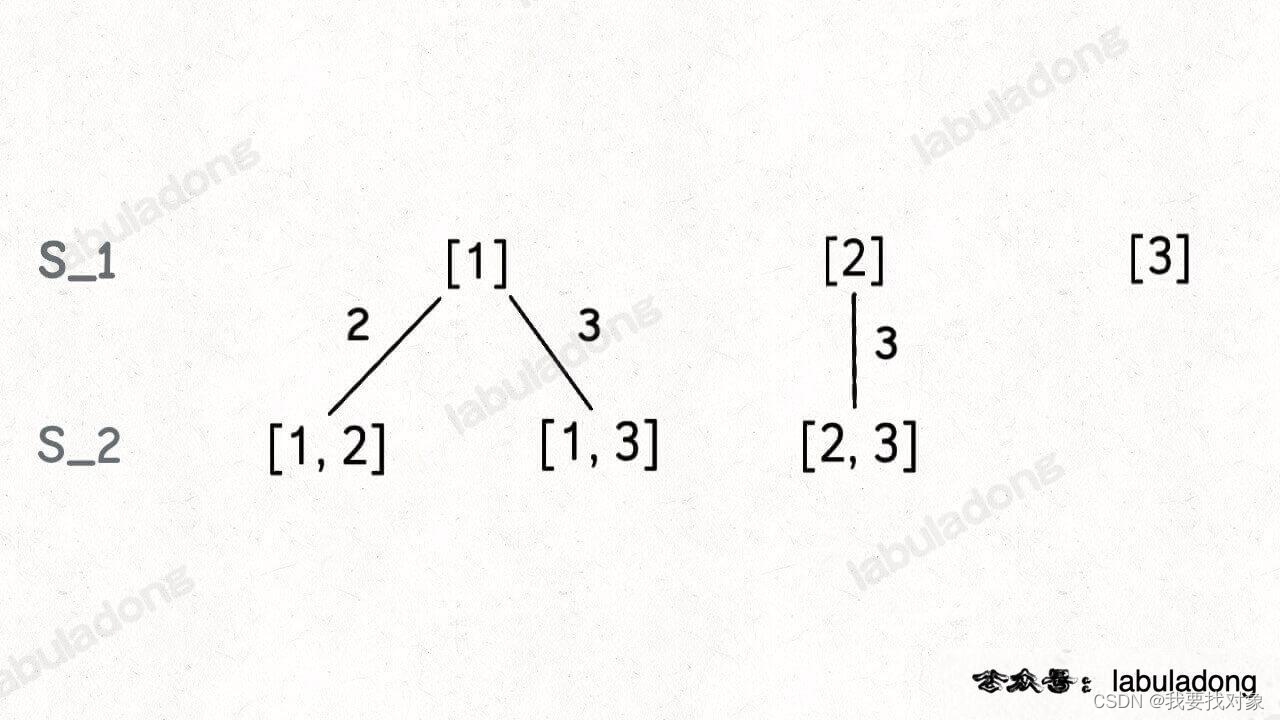
最后只有[1,2]可以继续衍生出三个元素的子集:
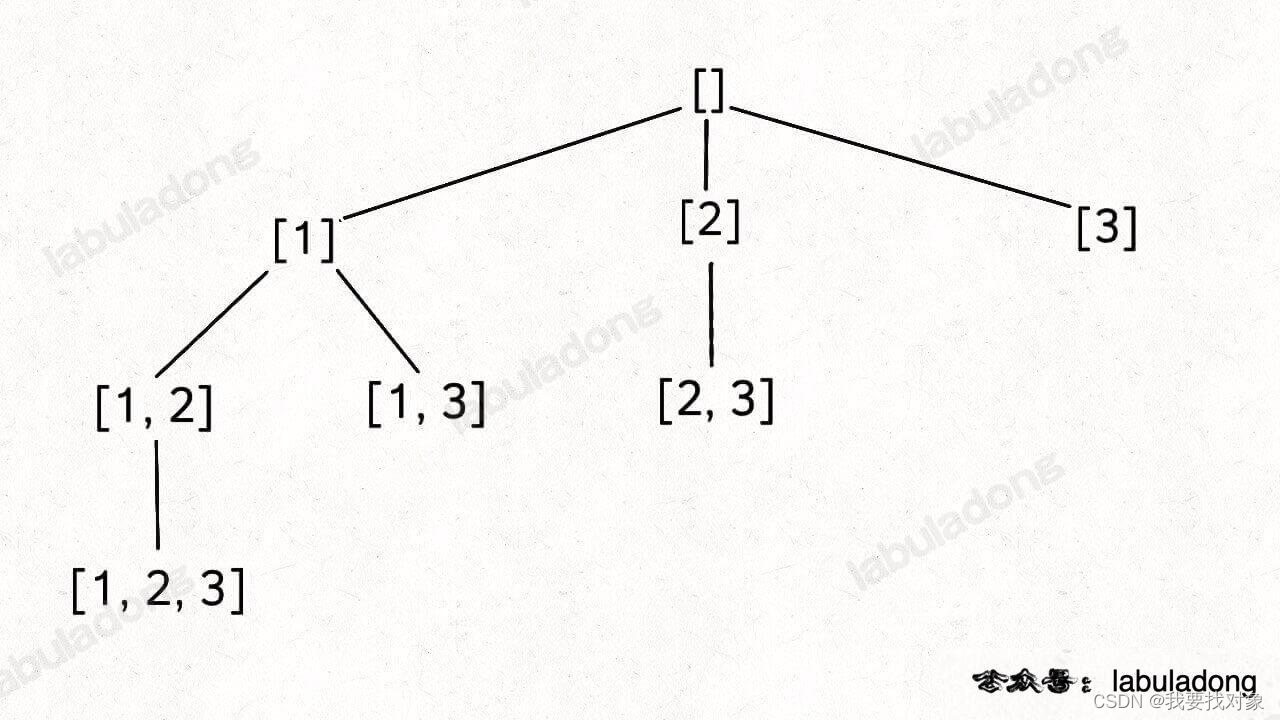
如果把根节点作为第 0 层,将每个节点和根节点之间树枝上的元素作为该节点的值,那么第 n 层的所有节点就是大小为 n 的所有子集。
这里让我们求所有的节点,可以理解为求解组合树的所有节点
class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();public List<List<Integer>> subsets(int[] nums) {backtrack(nums,0);return res;}//路径 由track记录//路径列表 比当前节点val大的值//结束条件 start == nums.lengthvoid backtrack(int[] nums,int start){res.add(new ArrayList(track));for(int i = start;i<nums.length;i++){track.add(nums[i]);backtrack(nums,i+1);track.removeLast();}}
}
1.2.4 组合(组合/子集问题)
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
1 <= n <= 20
1 <= k <= n
思路以及代码:
这道题和上面那个子集几乎一样,只是给了k并且不考虑空集
class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();public List<List<Integer>> combine(int n, int k) {backtrack(n,k,1);return res;}// 路径 track// 选择集合 比当前节点val大的// 结束条件 track.size == kpublic void backtrack(int n,int k,int start){if(track.size() == k){res.add(new ArrayList(track));return ;}for(int i = start;i<=n;i++){track.add(i);backtrack(n,k,i+1);track.removeLast();}}
}
1.2.5 全排列 (排列问题)1.2.1做过
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
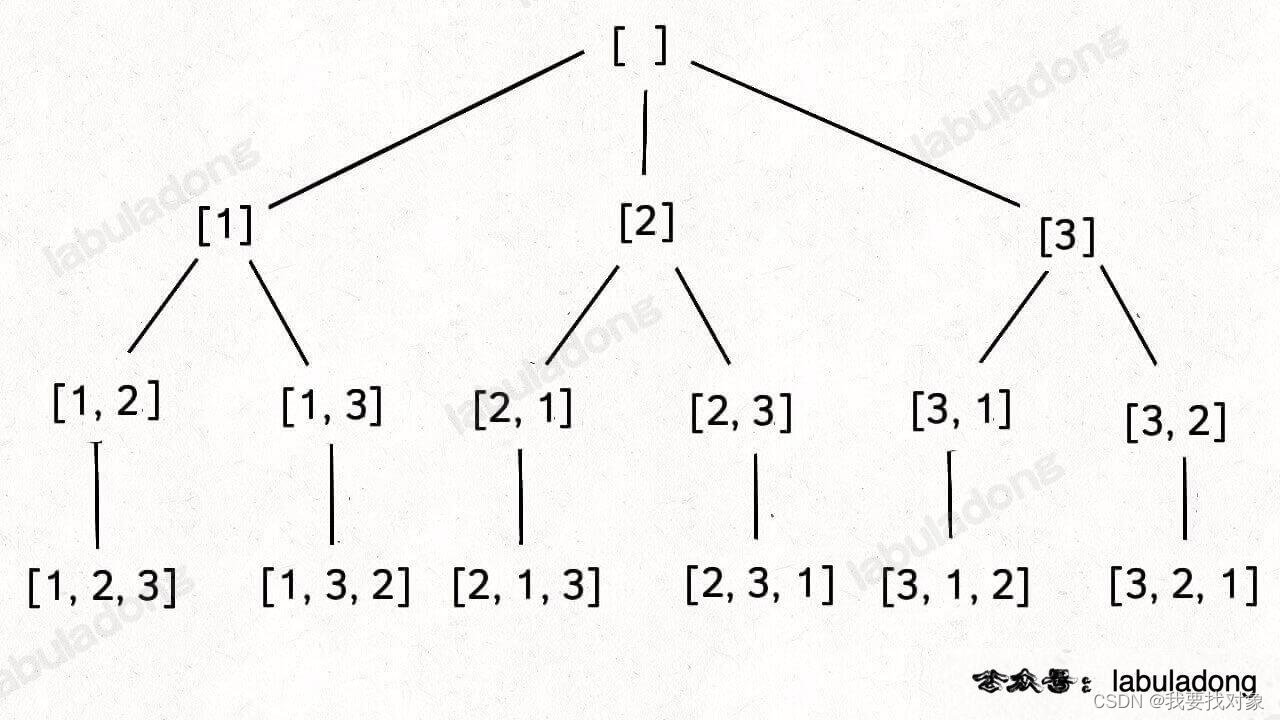
对于排列问题,只需要用 used 数组标记已经在路径上的元素避免重复选择,然后收集所有叶子节点上的值,就是所有全排列的结果。
1.2.6 子集II (可重复元素的组合/子集)
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
代码以及思路:
这道题首先两个点:
-
给出的集合可以无序:
说明你要先给nums排序 -
给出的nums可以有重复,但是子集不可以重复(例如nums=[1,2,2] 子集里可以出现[2,2],但是不能出现两个[2]):
需要剪纸,剪纸时机:同一层出现两个val相同的结点
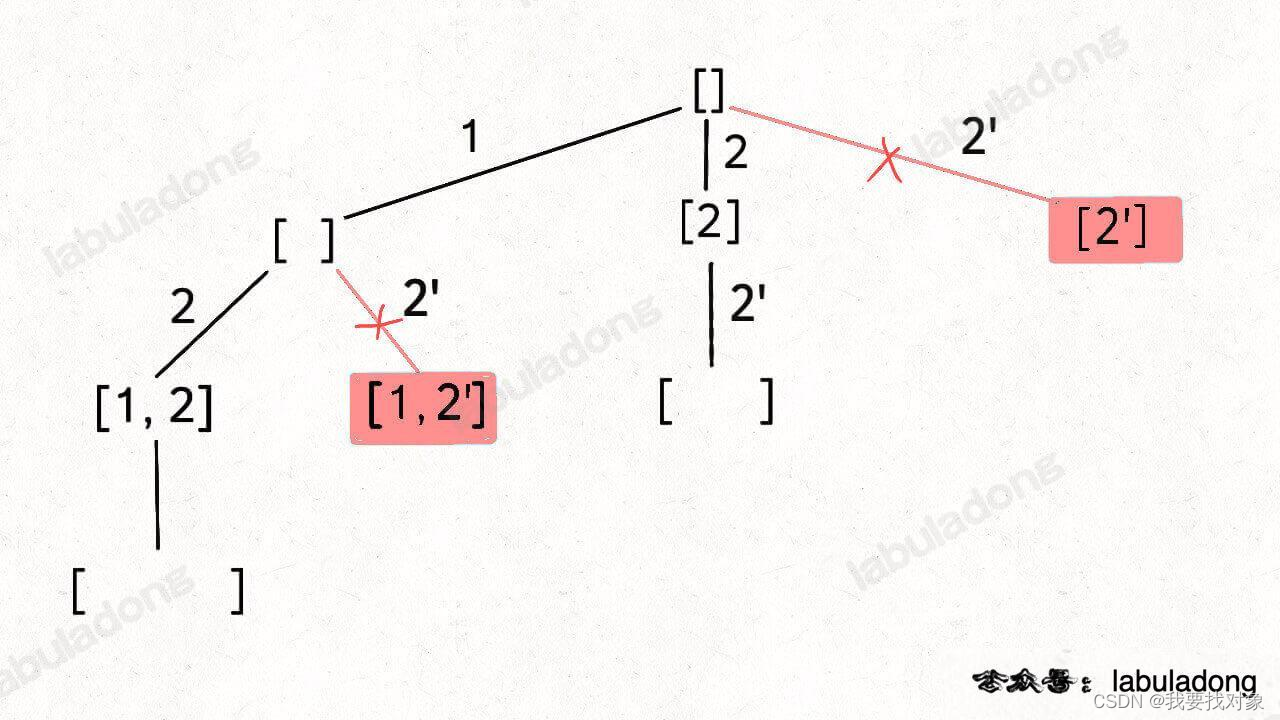
class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();public List<List<Integer>> subsetsWithDup(int[] nums) {Arrays.sort(nums);backtrack(nums,0);return res;}//路径 track//路径选择 当同层出现相同val节点,不进行选择//结束 遍历完成public void backtrack(int[] nums,int start){res.add(new ArrayList(track));for(int i = start;i<nums.length;i++){//当同层出现相同val节点,进行剪纸if(i > start && nums[i] == nums[i-1]){continue;}track.add(nums[i]);backtrack(nums,i+1);track.removeLast();}}
}
1.2.7 排列组合II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
思路以及代码:
这道题就是集合有重复元素 且 让子集和为target
做法很简单,保证子集不出现重复子集的情况下,只要额外用一个 trackSum 变量记录回溯路径上的元素和
class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();int tracksum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {if(candidates.length == 0){return res;}Arrays.sort(candidates);backtrack(candidates,target,0);return res;}void backtrack(int[] candidates,int target,int start){if(tracksum == target){res.add(new ArrayList(track));return ;}if(tracksum > target){return ;}for(int i = start;i<candidates.length;i++){if(i > start && candidates[i] == candidates[i-1]){continue;}track.add(candidates[i]);tracksum+=candidates[i];backtrack(candidates,target,i+1);track.removeLast();tracksum-=candidates[i];}}
}
1.2.7 全排列 II (排列题型)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
思路以及代码:
对比一下之前的标准全排列解法代码,这段解法代码只有两处不同:
1、对 nums 进行了排序。
2、添加了一句额外的剪枝逻辑。
这里的剪纸很有讲究:
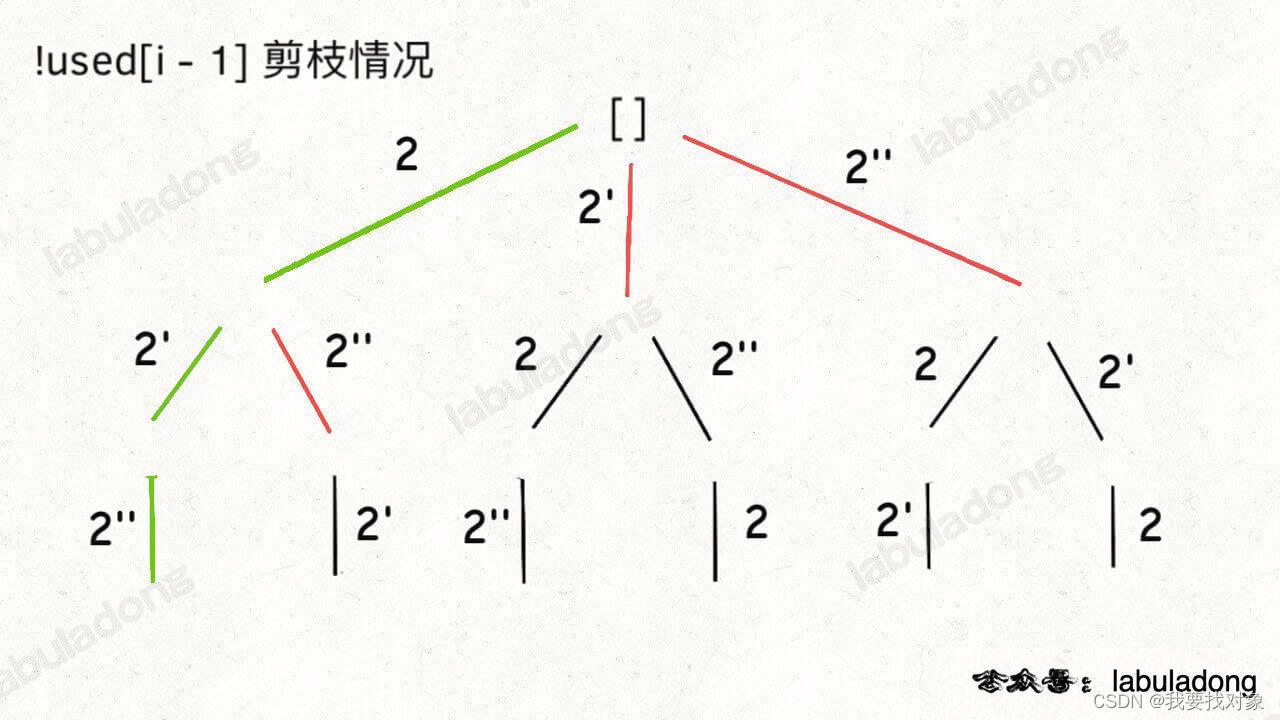
相同元素在排列中的相对位置保持不变。
比如说 nums = [1,2,2’] 这个例子,我保持排列中 2 一直在 2’ 前面。
当出现重复元素时,比如输入 nums = [1,2,2’,2’‘],2’ 只有在 2 已经被使用的情况下才会被选择,同理,2’’ 只有在 2’ 已经被使用的情况下才会被选择,这就保证了相同元素在排列中的相对位置保证固定。
// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {// 如果前面的相邻相等元素没有用过,则跳过continue;
}
// 选择 nums[i]class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);used = new boolean[nums.length];backtrack(nums);return res;}void backtrack(int[] nums){if(track.size() == nums.length){res.add(new ArrayList(track));return;}for(int i = 0;i<nums.length;i++){if(used[i] == true){continue;}//因为集合中有重复元素 所以剪枝 !!!固定相同的元素在排列中的相对位置if(i > 0 && nums[i] == nums[i-1] && !used[i-1]){continue;}used[i] = true;track.add(nums[i]);backtrack(nums);track.removeLast();used[i] = false;}}
}
1.2.8 组合总和 (子集/组合(元素无重可复选))
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
代码和思路:
首先我们回顾下,普通的子集/组合如何防止重复使用集合的元素?
控制进入下一层递归树的元素,也就是这个 i 从 start 开始,那么下一层回溯树就是从 start + 1 开始,从而保证 nums[start] 这个元素不会被重复使用:
// 无重组合的回溯算法框架
void backtrack(int[] nums, int start) {for (int i = start; i < nums.length; i++) {// ...// 递归遍历下一层回溯树,注意参数backtrack(nums, i + 1);// ...}
}
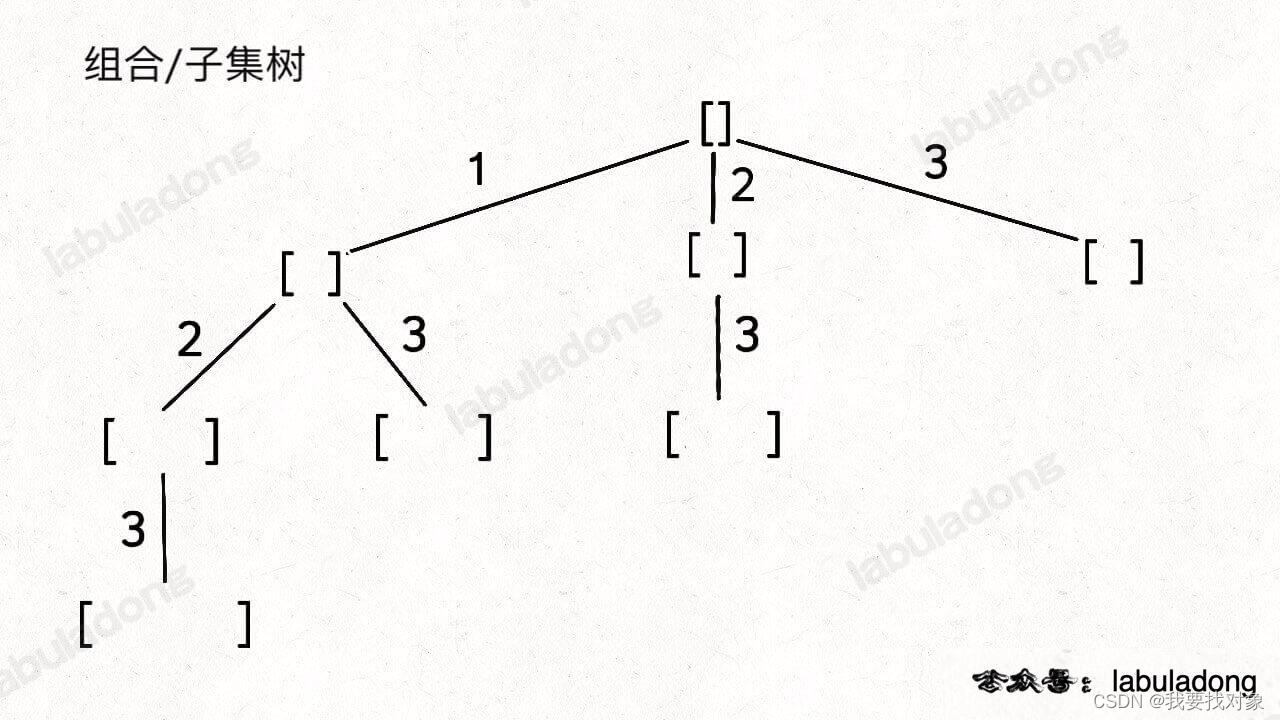
因此,如果要是可以选择重复元素的话,只要把 i + 1 改成 i 即可:
// 可重组合的回溯算法框架
void backtrack(int[] nums, int start) {for (int i = start; i < nums.length; i++) {// ...// 递归遍历下一层回溯树,注意参数backtrack(nums, i);// ...}
}
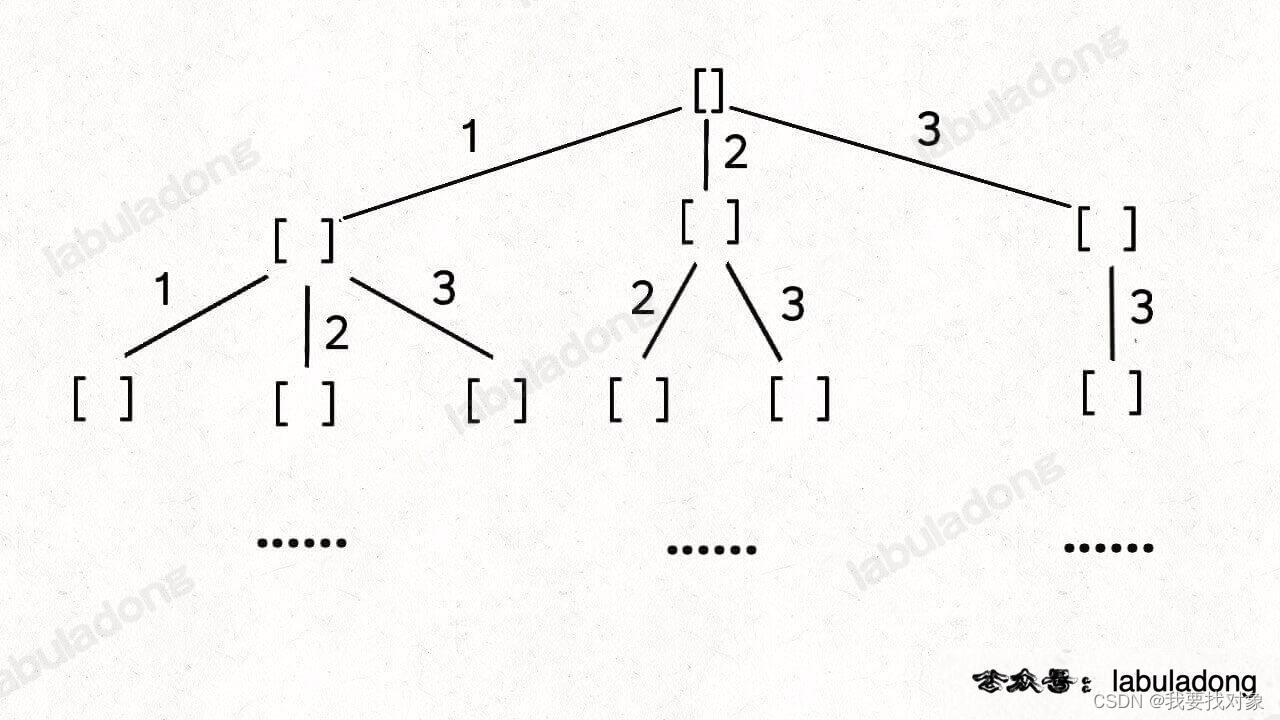
总代码:
class Solution {List<List<Integer>> res = new ArrayList();List<Integer> track = new ArrayList();int tracksum = 0;public List<List<Integer>> combinationSum(int[] candidates, int target) {trackback(candidates,target,0);return res;}public void trackback(int[] nums,int target,int start){if(tracksum == target){res.add(new ArrayList(track));return ;}if(tracksum > target){return ;}for(int i = start;i<nums.length;i++){tracksum += nums[i];track.add(nums[i]);trackback(nums,target,i);tracksum -= nums[i];track.removeLast();}}
}
1.2.9 排列(元素无重可复选)
以此类推,标准的全排列算法利用 used 数组进行剪枝,避免重复使用同一个元素。如果允许重复使用元素的话,直接放飞自我,去除所有 used 数组的剪枝逻辑就行了。